Ayesha is standing atop a vertical tower 200m high and observes a car moving away from the tower on a straight, horizontal road from the foot of the tower. At 11:00 AM, she observes the angle of depression of the car to be $$45^{\circ}$$. At 11:02 AM, she observes the angle of depression of the car to be $$30^{\circ}$$. The speed at which the car is moving is approximately
Solution
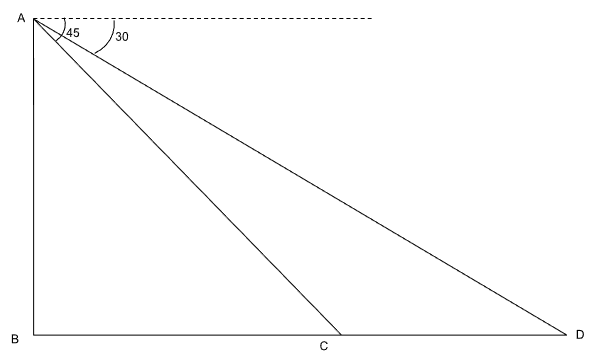
AB = 200 m, angle ACB = 45 and angle ADB = 30, using the alternate opposite angles theorem.
At 11:00 AM, she is at point C, and at 11:02 AM, she is at point D. This means that she covers the distance CD in 2 minutes (120 seconds).
=> Speed of Ayesha = CD/120 m/s
$$\tan\left(45\right)=\dfrac{AB}{BC}$$ => $$1=\frac{200}{BC}$$ => $$BC=200$$
$$\tan\left(30\right)=\dfrac{AB}{BD}$$ => $$\dfrac{1}{\sqrt{3}}=\dfrac{200}{BC+CD}$$ => $$200+CD=200\sqrt{3}$$ => $$CD=200\left(\sqrt{3}-1\right)$$
=> Speed of Ayesha = $$\dfrac{200\left(\sqrt{3}-1\right)}{120}$$ m/s
Since we need the speed in km/hr, we will multiply the above by 18/5 to get the speed in km/hr.
=> Speed of Ayesha = $$\frac{200\left(\sqrt{3}-1\right)}{120}\times\frac{18}{5}$$ km/hr
=> Speed of Ayesha = 4.392 km/hr
Create a FREE account and get:
- Download Maths Shortcuts PDF
- Get 300+ previous papers with solutions PDF
- 500+ Online Tests for Free

