The function $$f(x) = \dfrac{x^{3} - 5x^{2} - 8x}{3}$$ is

Given, $$f(x) = \dfrac{x^{3} - 5x^{2} - 8x}{3}$$

so, $$f(x)=\dfrac{x\left(x^2-5x-8\right)}{3}$$

Let's find the roots of the quadratic $$x^2-5x-8=0$$

Roots of this equation are $$\dfrac{5+\sqrt{\ 5^2-4\times\ \left(-8\right)}}{2}$$ and $$\dfrac{5-\sqrt{\ 5^2-4\times\ \left(-8\right)}}{2}$$

or, roots of this equation are $$\dfrac{5+\sqrt{57\ }}{2}$$ and $$\dfrac{5-\sqrt{57\ }}{2}$$

So, $$f\left(x\right)=x\left(x-\dfrac{5-\sqrt{\ 57}}{2}\right)\left(x-\dfrac{5+\sqrt{\ 57}}{2}\right)$$

So, roots of the equation $$f(x)=0$$ are 0,$$\dfrac{5+\sqrt{57\ }}{2}$$ and $$\dfrac{5-\sqrt{57\ }}{2}$$

Approximately, $$\dfrac{5+\sqrt{57\ }}{2}=6.27$$ and $$\dfrac{5-\sqrt{57\ }}{2}=-1.27$$

Taking a value greater than $$\dfrac{5+\sqrt{57\ }}{2}$$, we can see $$f(x)>0$$

Taking a value in between 0 and $$\dfrac{5+\sqrt{57\ }}{2}$$, we can see $$f(x)<0$$

Similarly, taking a value between $$\dfrac{5-\sqrt{57\ }}{2}$$ and 0, we can see $$f(x)>0$$

Taking a value lesser than $$\dfrac{5-\sqrt{57\ }}{2}$$. we can see $$f(x)<0$$

So, we can draw the graph of $$f(x)$$ like:

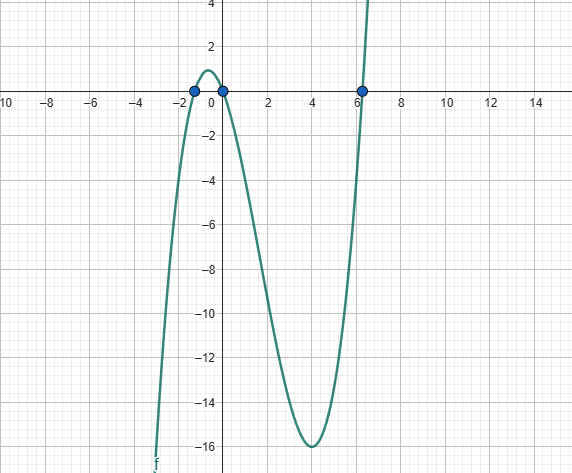
We can see for $$x$$ lesser than $$\dfrac{5-\sqrt{\ 57}}{2}$$ the function is monotonically decreasing and negative.

For $$x$$ greater than $$\dfrac{5+\sqrt{\ 57}}{2}$$ the function is monotonically increasing and positive.

So, option C is the correct answer.