Sign in
Please select an account to continue using cracku.in
↓ →
10 players - P1, P2, … , P10 - competed in an international javelin throw event. The number (after P) of a player reflects his rank at the beginning of the event, with rank 1 going to the topmost player. There were two phases in the event with the first phase consisting of rounds 1, 2, and 3, and the second phase consisting of rounds 4, 5, and 6. A throw is measured in terms of the distance it covers (in meters, up to one decimal point accuracy), only if the throw is a ‘valid’ one. For an invalid throw, the distance is taken as zero. A player’s score at the end of a round is the maximum distance of all his throws up to that round. Players are re-ranked after every round based on their current scores. In case of a tie in scores, the player with a prevailing higher rank retains the higher rank. This ranking determines the order in which the players go for their throws in the next round.
In each of the rounds in the first phase, the players throw in increasing order of their latest rank, i.e. the player ranked 1 at that point throws first, followed by the player ranked 2 at that point and so on. The top six players at the end of the first phase qualify for the second phase. In each of the rounds in the second phase, the players throw in decreasing order of their latest rank i.e. the player ranked 6 at that point throws first, followed by the player ranked 5 at that point and so on. The players ranked 1, 2, and 3 at the end of the sixth round receive gold, silver, and bronze medals respectively.
All the valid throws of the event were of distinct distances (as per stated measurement accuracy). The tables below show distances (in meters) covered by all valid throws in the first and the third round in the event.
Distances covered by all the valid throws in the first round

Distances covered by all the valid throws in the third round

The following facts are also known.
i. Among the throws in the second round, only the last two were valid. Both the throws enabled these players to qualify for the second phase, with one of them qualifying with the least score. None of these players won any medal.
ii. If a player throws first in a round AND he was also the last (among the players in the current round) to throw in the previous round, then the player is said to get a double. Two players got a double.
iii. In each round of the second phase, exactly one player improved his score. Each of these improvements was by the same amount.
iv. The gold and bronze medalists improved their scores in the fifth and the sixth rounds respectively. One medal winner improved his score in the fourth round.
v. The difference between the final scores of the gold medalist and the silver medalist, as well as the difference between the final scores of the silver medalist and the bronze medalist was 1.0 m.
Let us arrange the players in the order in which they throw in each round.
Round 1: Here the players throw in order of their initial seeds so the order is as follows:
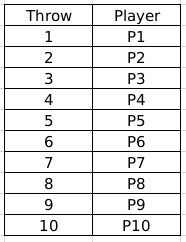
So, their rank at the start of Round 2 is in order of their throws in the first round. Also, we need to consider the same order for people having invalid throws.
Round 2: P2, P4, P8, P10 had the same relative rankings since they all have invalid throws, that is, 0 metres. Rest are arranged as per their throw distances.
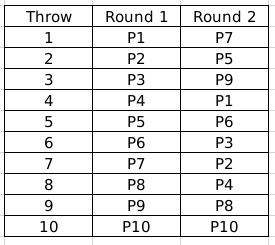
Now, in round 2, only P8 and P10 had valid throws. Hence, their order will change at the start of Round 3, however, the remaining order stays the same. That is, P8 and P10 will move up in the table and occupy some higher places, whereas some of the others may move down consequently.
Round 3: In Round 3, we can see that P1 improved his score from 82.9 to 88.6. The other 2 participants did not improve their scores. Also after Round 3, P8 and P10 qualify, where one of P8 or P10 is at the sixth position. So at the end of Round 3, we can say that P6, P3, P2, and P4 are at the bottom 4 positions(ranks). One of P8 or P10 is at the sixth position. P1 > P7 > P5 > P9.
So at the end of round 3, the ranks are as follows:

The other person between P8/P10 can go anywhere between Rank 1 and Rank 5.
Now let us consider the two players who got a double. Doubles happen in the transition between rounds.
1 -> 2 - Not possible
2 -> 3 - Possible if P10 reaches Rank 1 after round 2.
3 -> 4 - P8/P10 who is the last among qualifying will be the first to throw. So, here it definitely happens.
4 - > 5 AND 5 - > 6 not possible.
So, after Round 2, definitely, P10 reaches the top of the ranking. P8 is at the bottom. Hence, after Round 3, P10 either retains rank 1 or P1 surpasses him and P10 becomes Rank 2.
So, two combinations are possible at the end of Round 3:
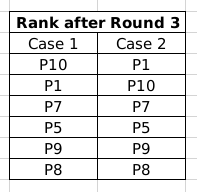
Now, we know that in each of the rounds in phase 2, only one player improves his score. Also, P8 and P10 cannot win medals. Hence, in case 1, three of P1, P7, P5 and P9 will improve their scores by x and reach the top 3 positions. However, the top 3 positions' distances are in AP.
P1 - 88.6 + x
P7 - 87.2 + x
P5 - 86.4 + x
P9 - 84.1 + x
The differences do not satisfy the condition. Hence, case 1 is invalidated.
Case 2: Here, P1 definitely wins a medal, and P10 does not. So, two of P7, P5 and P9 jumps above P10. Now, if we have three different people increasing their scores or distances in each of the three rounds, again we would not get a difference of 1 among the Gold, Silver and Bronze medallists. Hence, one of them increases his score twice and the other increases his score twice and none of them is P1.
Let us take the cases where P1 is individually the G, S and B medallists.
Case 1: P1 is a G medallist.
P1 - 88.6
The silver medallist is 87.6 and the bronze medallist is 86.6 metres. However, P10 has thrown for a distance that is greater than 87.2 metres. Hence, in this case, he would be the B medallist. Hence, this is not the right case.
Case 2: P1 is the S medallist.
P1 - 88.6
G - 89.6
B - 87.6
Now, if we see the differences
89.6 - 87.2 = 2.4
87.6 - 86.4 = 1.2
This satisfies the condition that P7 has increased his score twice to become the gold winner and P5 has increased it once to become the bronze winner.
Hence, P1 - Silver
P7 - Gold
P5 - Bronze
Hence, P1 won the silver medal.

Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation