The Set of real values of x for which the inequality $$\log_{27}8\le\log_3x<9^{\ \frac{\ 1}{\log_23}}$$ holds is
Solution
Lets use the properties of logarithms :
$$\log_ba\ =\dfrac{\ 1}{\log_ab}\ ,\ \ n\log_ba\ =\log_ba^n\ \&\ \ \log_{b^n}a\ =\frac{\ 1}{n}\log_ba,\ \ \ b^{\log_ba}=a$$
Now, the inequality can be written as :
$$\log_{27}8\le\log_3x<9^{\ \frac{\ 1}{\log_23}}$$
$$\log_{3^3}2^3\ \le\ \log_3X\ \ <\ 9^{\log_32}$$
this implies : $$\log_32\ \le\ \log_3X\ \ <\ 3^{2\left(\log_32\right)}$$
$$\log_32\ \le\ \log_3X\ \ <\ 3^{\log_34}$$
$$\log_32\ \le\ \log_3X\ \ <\ 4$$
This implies that, $$X\ \ge\ 2\ \&\ X\ <\ 3^4$$
Therefore, X lies in [2,81) .
Video Solution
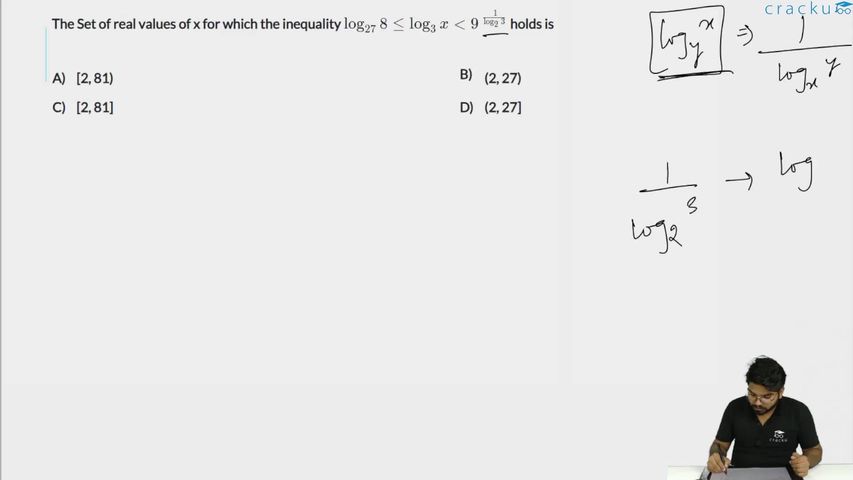
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
- Download Maths Shortcuts PDF
- Get 300+ previous papers with solutions PDF
- 500+ Online Tests for Free

