In a class of 65 students 40 like cricket, 25 like football and 20 like hockey. 10 students like both cricket and football, 8 students like football and hockey and 5 students like all three sports. If all the students like at least one sport, then the number of students who like both cricket and hockey is
Solution
Number of students playing all three sports = 5
So, number of students who like only cricket and football will be 10-5=5
number of students who like only football and hockey will be 8-5=3
Let, $$x$$ be the number of students who like only cricket and hockey.
We can make a Venn diagram and fill it like:
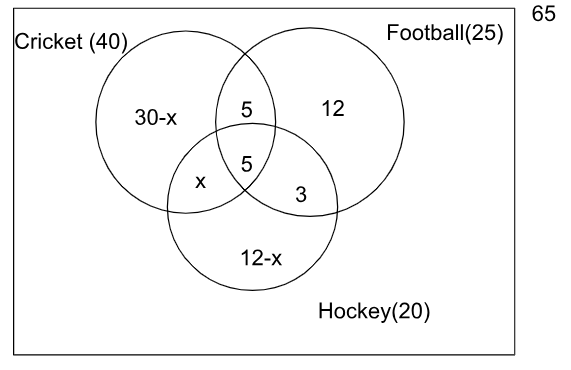
So, $$\left(30-x\right)+x+\left(12-x\right)+25=65$$
or, $$42-x=40$$
or, $$x=2$$
So, number of students who like both cricket and hockey = $$x+5=2+5=7$$
Create a FREE account and get:
- Download Maths Shortcuts PDF
- Get 300+ previous papers with solutions PDF
- 500+ Online Tests for Free

