Solution
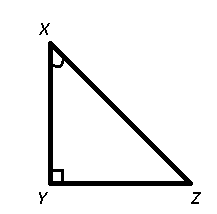
Given : $$\cot X$$ = $$\frac{5}{12}$$
Also, $$\cot X=\frac{XY}{YZ}=\frac{5}{12}$$
Let XY = 5 cm and YZ = 12 cm
Thus, in $$\triangle$$ XYZ, => $$(XZ)^2=(XY)^2+(YZ)^2$$
=> $$(XZ)^2=(5)^2+(12)^2$$
=> $$(XZ)^2=25+144=169$$
=> $$XZ=\sqrt{169}=13$$ cm
To find : $$\sec Z=\frac{XZ}{YZ}$$
= $$\frac{13}{12}$$
=> Ans - (C)
Get AI Help
Create a FREE account and get:
- Free SSC Study Material - 18000 Questions
- 230+ SSC previous papers with solutions PDF
- 100+ SSC Online Tests for Free
