Please enter the following details
Free Daily Targets & Mocks
Study Material & Formulas PDFs
1 on 1 Mentorship
Question 25
In ΔPQR measure of angle Q is $$90^\circ$$. If $$cot P = \frac{8}{15}$$, and PQ = 4cm, then what is the length (in cm) of side PR?
Solution
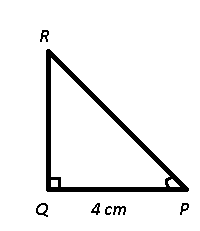
Given : PQ = 4 cm and $$cot P = \frac{8}{15}$$
To find : PR = ?
Solution : In right $$\triangle$$ PQR,
=> $$cot(P)=\frac{PQ}{QR}$$
=> $$\frac{8}{15}=\frac{4}{QR}$$
=> $$QR=\frac{15}{8}\times4=7.5$$ cm
$$\therefore$$ $$(PR)^2=(PQ)^2+(QR)^2$$
=> $$(PR)^2=(4)^2+(7.5)^2$$
=> $$(PR)^2=16+56.25=72.25$$
=> $$PR=\sqrt{72.25}=8.5$$ cm
=> Ans - (A)
Create a FREE account and get:
- Free SSC Study Material - 18000 Questions
- 230+ SSC previous papers with solutions PDF
- 100+ SSC Online Tests for Free
