Which of the following straight lines are both tangent to the circle $$x^{2} + y^{2} − 6x + 4y − 12 = 0$$
Solution
The equation of circle is $$x^{2} + y^{2} − 6x + 4y − 12 = 0$$
We can compare this with standard equation of circle, $$x^2+y^2+2gx+2fy+c=0$$
so, $$g=-3\ ,\ f=2,\ c=-12$$
Now, centre of circle is $$\left(-g,-f\right)$$. So, centre will be $$\left(3,-2\right)$$
Radius of circle will be r = $$\sqrt{\ g^2+f^2-c}=\sqrt{\ 3^2+\left(-2\right)^2-\left(-12\right)}=\ \sqrt{\ 25\ }=5$$ units
Now for a line to be tangent to a circle, perpendicular distance from the centre of the circle to the line, should be equal to its radius.
For the line $$4x+3y+19=0$$, perpendicular distance from the centre = $$\dfrac{\left|4\left(3\right)+3\left(-2\right)+19\right|}{\sqrt{\ \left(4^2+3^2\right)}}=\dfrac{25}{5}=5\ $$ units = radius
So, $$4x+3y+19=0$$ is a tangent to the circle.
For the line $$4x+3y-31=0$$, perpendicular distance from the centre = $$\dfrac{\left|4\left(3\right)+3\left(-2\right)-31\right|}{\sqrt{\ \left(4^2+3^2\right)}}=\dfrac{25}{5}=5\ $$ units = radius
So, $$4x+3y-31=0$$ is also a tangent to the circle.
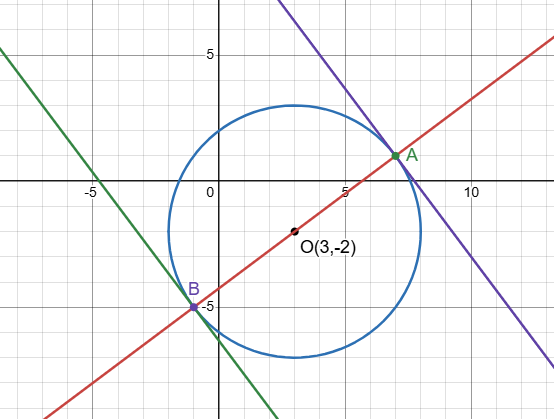
Centre of circle is $$\left(3,-2\right)$$
Purple colour line is $$4x+3y-31=0$$
Green colour line is $$4x+3y+19=0$$
OA and OB are radii perpendicular to the respective tangents.
Create a FREE account and get:
- Download Maths Shortcuts PDF
- Get 300+ previous papers with solutions PDF
- 500+ Online Tests for Free

