Sign in
Please select an account to continue using cracku.in
↓ →
The Hi-Lo game is a four-player game played in six rounds. In every round, each player chooses to bid Hi or Lo. The bids are made simultaneously. If all four bid Hi, then all four lose 1 point each. If three players bid Hi and one bids Lo, then the players bidding Hi gain 1 point each and the player bidding Lo loses 3 points. If two players bid Hi and two bid Lo, then the players bidding Hi gain 2 points each and the players bidding Lo lose 2 points each. If one player bids Hi and three bid Lo, then the player bidding Hi gains 3 points and the players bidding Lo lose 1 point each. If all four bid Lo, then all four gain 1 point each. Four players Arun, Bankim, Charu, and Dipak played the Hi-Lo game. The following facts are known about their game:
1. At the end of three rounds, Arun had scored 6 points, Dipak had scored 2 points, Bankim and Charu had scored -2 points each.
2. At the end of six rounds, Arun had scored 7 points, Bankim and Dipak had scored -1 point each, and Charu had scored -5 points.
3. Dipak’s score in the third round was less than his score in the first round but was more than his score in the second round.
4. In exactly two out of the six rounds, Arun was the only player who bid Hi.
Let 'H' represents Hi and 'L' represents Lo.
Given if they bid
Case 1: HHHH then all players gets -1 points.
Case 2: HHHL => H gets +1 and L gets -3.
Case 3: HHLL => H gets +2 and L gets -2.
Case 4: HLLL => H gets +3 and L gets -1.
Case 5: LLLL => every player gets +1.
From the given information we can draw the following table:
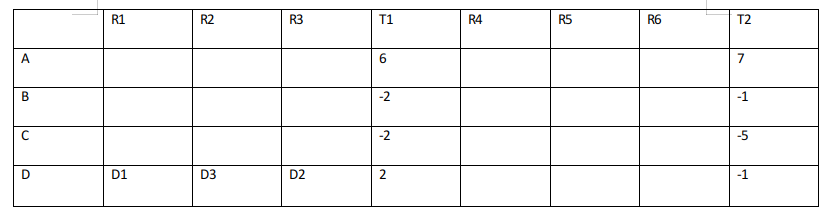
**T1 is the cumulative of points till Round 3 and T2 is sum of points till round 6.
**Arun, Bankim, Charu, and Dipak are represented by A, B, C, D respectively.
From point 3, D1>D2>D3
D scored 2 points till round R3 and D1>D3>D2 the possible scenarios are :
Case D1: 3,2,-3
In this case the points of A in R1, R3, R2 will be -1,2/-2, 1 in any possible combination the sum will not be 6. So, this case is invalid.
Case D2: 2,1,-1
In this case the points of A in R1, R3, R2 will be 2/-2, 1/-3, -1/3 so, if the points in R1, R3, R2 are 2,1,3 the case is valid and no other cases are possible.
Case D3: 3,1,-2
In this case the points of A in R1, R3, R2 will be -1, 1/-3/1, 2/-2
in any possible combination the sum will not be 6. So, this case is
invalid.
.'. Points of A,D in (R1,R2,R3) are (2,3,1) and (2,-1,1) respectively.
Since A got +3 in R2, he is only the one to bid h in R2 and points of B and C in round 2 are -1,-1 i.e they bid L, L.
Since A and D got 2 points each in R1, C and B must have got -2, -2 i.e they bid L, L.
Since A and D got 1 point in R3, C and B must also have got 1 in R3 i.e they bid L, L.
With this data, the table now looks like:

No information is given about the individual scores in R4, R5, R6.
Given In exactly two out of the six rounds, Arun was the only player who bid Hi.
Let R.x, R.y, R.z represent R4, R5, R6 in any order.
Let A bid H in R.x=> B,C,D bid L.
The table now looks like:

For A, R.x+R.y+R.z=1 => R.y+R.z=-2
For B, R.x+R.y+R.z=1 => R.y+R.z=2
For C, R.x+R.y+R.z=-3 => R.y+R.z=-2
For D, R.x+R.y+R.z=-3.=> R.y+R.z=-2
(R.y, R.z) for A can be (-3,1) or (-1,-1)
Case A1:
If for A, (R.y, R.z)=(-3,1)
Since for both C,D: R.y+R.z=-2
We can't get any combination such that the total points of B,C,D are obtained.
Case A2:
If for A, (R.y, R.z)=(-1,-1).the (R.y, R.z) of B,C,D can be (3,-1), (-1,-1), (-1,-1) and they must have bid (H,H), (L,H), (L,H) respectively while A must have bid (L, H)
Hence this case is valid.
The final table looks like:
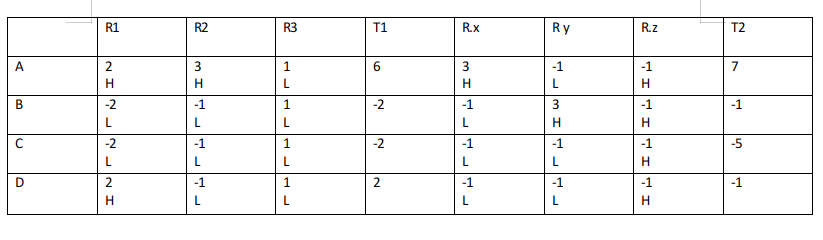
All the players made identical bids in R3 and R.z

Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation