ABCD is a quadrilateral whose diagonals AC and BD intersect at O. If triangles AOB and COD have areas 4 and 9 respectively, then the minimum area that ABCD can have is

ABCD is a quadrilateral whose diagonals AC and BD intersect at O. If

triangles AOB and COD have areas 4 and 9 respectively, then the minimum

area that ABCD can have is

It is given that ABCD is a quadrilateral whose diagonals AC and BD intersect at O.

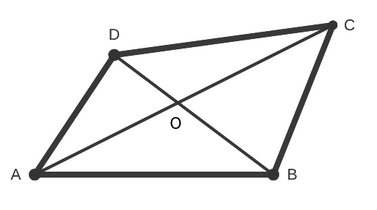
Now, Triangles AOB and COD have areas 4 and 9, respectively.

We need to find out the minimum area that ABCD can have is

We know ar ABCD = ar AOB + ar COD + ar BOC + ar AOD

In any quadrilateral, when the diagonals are drawn, they divide the quadrilateral into four triangles. The product of the areas of two opposite triangles is equal to the product of the areas of the other two opposite triangles

Thus, (ar AOB)*(ar COD) = (ar BOC)*(ar AOD)

(ar BOC)*(ar AOD) = 4*9 = 36

The sum has to be minimum, and the product of ar BOC and ar AOD is 36.

This will happen when both areas are equal

Thus, ar BOC = 6 = ar AOD

Therefore, the minimum area that ABCD can have is = 4+9+6+6 = 25