A child is looking for his father. He went 90 m in the East before turning to his right. He went 20 m before turning to his right again to look for his father at his uncle's place 30 m from this point. His father was not there. From there, he went 100 m to the North before meeting his father in a street. How far did the son meet his father from the starting point?

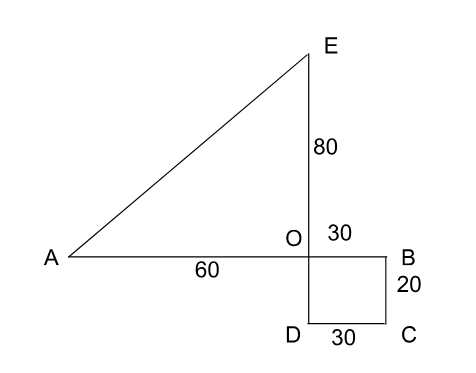
The child starts from point A and he moves 90 m in the east and reaches at B.

Now, from B he takes a right and moves 20 m and reaches at C.

Then, again he takes a right and moves 30 m to reach at D. (Uncle's place)

Now, he moves 100 m north of point D, and reaches at E.

We need to find the distance AE?

From the diagram, we know AEO forms a right-angled triangle.

AO = 60

EO = 80

Thus, $$AE^2=AO^2+EO^2$$

$$AE^2=60^2+80^2$$

AE = 100 m