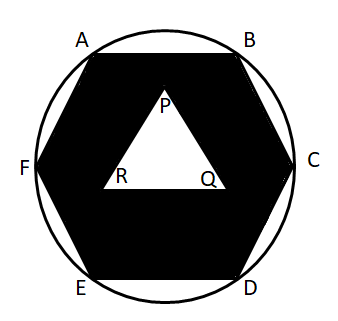
ABCDEF is a regular hexagon of side a and PQR is an equilateral triangle. The area of the shaded portion is X and CD : PQ : : 2 : 1. Find the area of the circle circumscribing the hexagon in terms of X.
Solution
Let 'a' be the length of side of the hexagon. Therefore, the area of hexagon = $$6*\dfrac{\sqrt{3}}{4}\times a^2$$.
The area of triangle PQR = $$\dfrac{\sqrt{3}}{4}\times (a/2)^2$$
Therefore, the are of the shaded region = $$6*\dfrac{\sqrt{3}}{4}\times a^2$$ - $$\dfrac{\sqrt{3}}{4}\times (a/2)^2$$ = $$\dfrac{23\sqrt{3}a^2}{16} = X$$
$$\Rightarrow$$ $$a^2 = \dfrac{16X}{23\sqrt{3}}$$
The area of the circle = $$\pi*a^2$$
$$\Rightarrow$$ $$\dfrac{16 \pi}{23 \sqrt{3}}$$ X. Hence, option A is the correct answer.
