Mohan was playing with a square cardboard of side 2 metres. While playing, he sliced off the corners of the cardboard in such a manner that a figure having all its sides equal was generated. The area of this eight sided figure is:

We can see that we will get a regular octagon as shown in the figure below. 

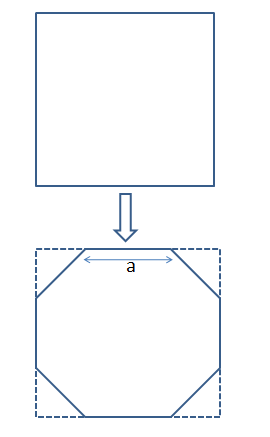
Let 'a' be the length of the side of the regular octagon. 

Hence, we can say that, $$\dfrac{a}{\sqrt{2}}+a+\dfrac{a}{\sqrt{2}} = 2$$

$$\Rightarrow$$ $$a = \dfrac{2}{\sqrt{2}+1}$$. 

Area of a regular octagon = $$2*(1+\sqrt{2})*a^2$$

$$\Rightarrow$$ $$2*(1+\sqrt{2})*(\dfrac{2}{\sqrt{2}+1})^2$$ 

$$\Rightarrow$$ $$\dfrac{8}{(\sqrt{2}+1)}$$.

Therefore, option D is the correct answer.