SSC CGL 18th August 2021 Shift-1
For the following questions answer them individually
Study the following table and answer the question:
Number of students Appeared (A) and Passed (P) in an annual examination from four schools Q, R, S & T in five years (2014 to 2018)
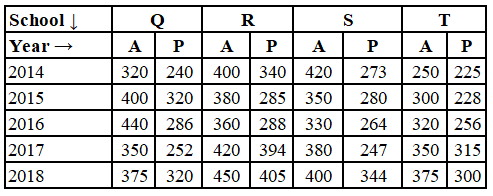
The total number of students passed from school Q in 2014 and 2018 is what percent less than the total number of students appeared from schools R and S in 2017?
If $$3 \sin^2 \theta - \cos \theta - 1 = 0, 0^\circ < \theta < 90^\circ$$, then what is the value of $$\cot \theta + \cosec \theta ?$$
Point P lies outside a circle with centre O. Tangents PA and PB are drawn to meetthe circle at A and respectively. If $$\angle APB = 80^\circ$$, then $$\angle OAB$$ is equal to:
If $$x^4 + y^4 + x^2y^2 = 21$$ and $$x^2 + y^2 - xy = 7$$, then what is the value of $$\frac{x}{y} + \frac{y}{x} ?$$
Simplify the following expression.
$$\frac{(375 + 125)^2 - (125 - 375)^2}{375 \times 375 - 125 \times 125}$$
Find the ratio between the fourth proportional of 12, 16, 6 and the third proportional of 4, 6.
Chord AB of circle of radius 10 cm is at a distance 8 cm from the centre O. If tangents drawn at A and B intersect at P, then the length of the tangent AP (in cm) is:
Study the following table and answer the question:
Number of students Appeared (A) and Passed (P) in an annual examination from four schools Q, R, S & T in five years (2014 to 2018)
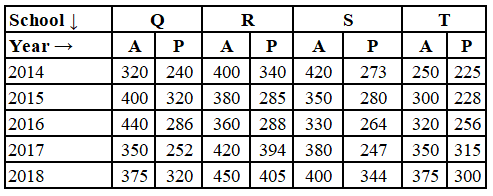
The ratio of the total number of students appeared from school Q in 2017 and from school S$ in 2018 to the total number of students passed from school R in 2018 and school T in 2014, is:
The following Bar Graphs represent the Export of Tea (in lakh tonnes) by two companies A and B during the years 2010 to 2015.
Study the chart and answer the question written below:
(Note: The data shown below is only for mathematical exercise. They do not represent the actual figures).
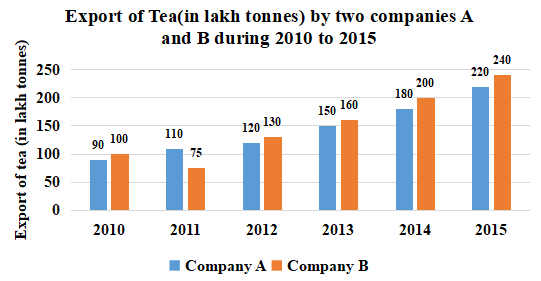
What is the ratio of the total exports of company B in 2011 and 2014 to the total exports of company A in 2012 and 2015?
The value of
$$(\sin 37^\circ \cos 53^\circ + \cos 37^\circ \sin 53^\circ) - \frac{4 \cos^2 37^\circ - 7 + 4 \cos^2 53^\circ}{\tan^2 47^\circ + 4 - \cosec^2 43^\circ}$$ is:
