The difference between compound and simple interests on a certain sum of money at the interest rate of 10 % per annum for $$1\frac{1}{2}$$ years is ₹183, when the interest is compounded semi-annually, then the sum of money is :
Solution
Let the Principal be Rs P
Simple interest = S.I. = $$\dfrac{P\times\ r\times\ t}{100}$$
or, S.I. = $$\dfrac{P\times\ 10\times\ \dfrac{3}{2}}{100}$$ = $$0.15 P$$
(time = $$1\dfrac{1}{2}$$ years = $$\dfrac{3}{2}$$ years)
Now calculating compound interest,
Principal = P
Rate = 10% p.a.
So, when compounded semi annually, rate = $$\left(\dfrac{10}{2}\%\right)$$= $$5\%$$
Also, in duration of $$1\dfrac{1}{2}$$ years, semi annually compounding will occur thrice.
So, compound interest = C.I. = $$P\left(1+\dfrac{5}{100}\right)^3-P$$
Now, according to question,
C.I. - S.I. = 183
So, $$P\left(1+\dfrac{5}{100}\right)^3-P$$ - $$0.15 P$$ = 183
or, $$P\left(1.05\right)^3-P-0.15P=183$$
or, $$0.007625P=183$$
or, $$P=₹24000$$
Video Solution
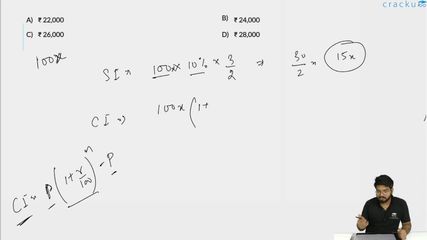
Click on the Email ☝️ to Watch the Video Solution