The cost of fencing of an equilateral triangular park and a square park is the same. If the area of the triangular park is $$16\sqrt{3} m^{2} $$, then the length of the diagonal of the square park is :
Solution
Let the side of equilateral triangle be 'a' cm.
We know, area of an equilateral triangle is given by the formula $$\dfrac{\sqrt{\ 3}}{4}\times\ a^2$$
Now, it is given, $$\dfrac{\sqrt{\ 3}}{4}\times\ a^2=16\sqrt{\ 3}$$
or, $$a^2=16\times\ 4=64$$
or, $$a=8$$
Now, perimeter of this equilateral triangle will be $$3\times\ 8=24$$ m
Now, it is given cost of fencing an equilateral triangular park and a square park is the same.
So, their perimeters will also be same (as cost of fencing depends on perimeter)
So, perimeter of square = 24 m
Now, perimeter of square = 4* side = 24 m
So, side of square = $$\dfrac{24}{4} m=6\ m$$
So, diagonal of the square park = side$$\sqrt{\ 2}$$ m = 6$$\sqrt{\ 2}$$ m.
Video Solution
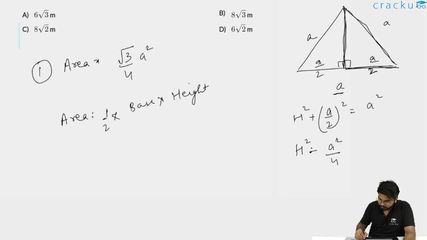
Click on the Email ☝️ to Watch the Video Solution