The set of all real values of x satisfying the inequality $$\frac{x^{2}(x + 1)}{(x - 1)(2x + 1)^{3}}> 0$$ is
Solution
Given inequality is,
$$\dfrac{x^{2}(x + 1)}{(x - 1)(2x + 1)^{3}}> 0$$ is
or, $$x^2\left(x+1\right)\left(x-1\right)\left(2x+1\right)^3>0$$
Now the terms in square are always positive. So we can eliminate them.
So, the inequality will be,
$$\left(x+1\right)\left(x-1\right)\left(2x-1\right)>0$$
Plotting the critical points $$x=-1,1,\frac{1}{2}$$ in number line and applying wavy-curve method we get,
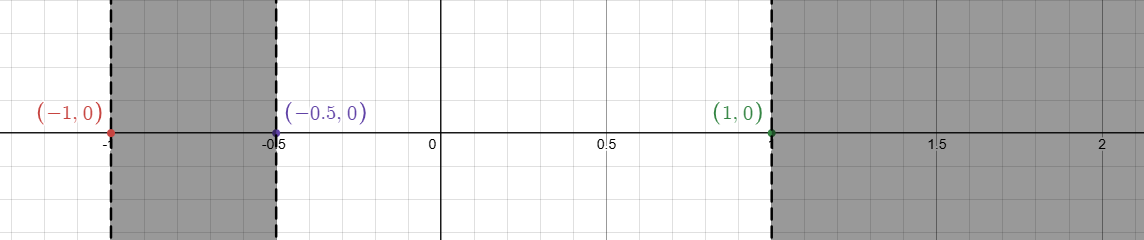
The black shaded region is the required domain of $$x$$
So, option A is the correct answer
Create a FREE account and get:
- Download Maths Shortcuts PDF
- Get 300+ previous papers with solutions PDF
- 500+ Online Tests for Free

