Question 31

A circle is inscribed in an equilateral triangle of side 24 cm, touching its sides. What is the area of the remaining portion of the triangle?

Solution

Based on the question, the following figure is obtained. The shaded area denotes the area that we need to find.

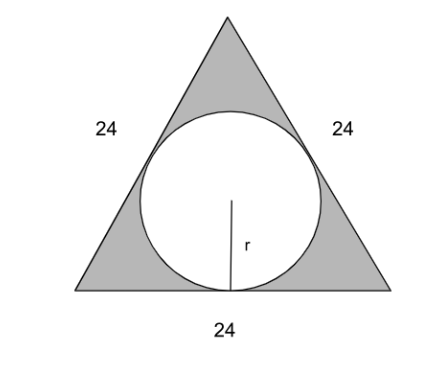
Screenshot 2025-08-28 12

Here, area of the equilateral triangle is $$A=\frac{\sqrt{\ 3}}{4}\left(side\right)^2=\frac{\sqrt{\ 3}}{4}\times\ 24^2=144\sqrt{\ 3}sq\ units$$

The inradius of the circle will be given by $$r=\frac{A}{s}$$ where A is the area of the triangle and s is the semi perimeter which is found to be $$\frac{24+24+24}{2}=36$$

So, $$r=\frac{144\sqrt{\ 3}}{36}=4\sqrt{\ 3}units$$

Hence, area of the circle is $$\pi\ \times\ \left(4\sqrt{\ 3}\right)^2=48\pi\ \ sq\ units$$

Finally, the area of the remaining area will be teh difference, which is $$144\surd{3} - 48 \pi cm^{2}$$ sq units. Hence , option A is the correct choice.

View More Questions From Temporary

Create a FREE account and get:

Download Maths Shortcuts PDF
Get 300+ previous papers with solutions PDF
500+ Online Tests for Free

maruti sir image

MAT Quant Questions | MAT Quantitative Ability

MAT Coordinate Geometry Questions MAT Logarithms Questions MAT Number Series Questions MAT Algebra Questions MAT Averages, Ratio and Proportion Questions MAT Quadratic Equations Questions MAT Time Speed Distance Questions MAT Number Systems Questions MAT Functions, Graphs and Statistics Questions MAT Linear Equations Questions MAT Data Sufficiency Questions MAT Arithmetic Questions MAT Time, Speed and Distance Questions MAT Remainders Questions MAT Logarithms, Surds and Indices Questions MAT Percentages Questions MAT Averages Questions MAT Geometry Questions MAT Time And Work Questions MAT Profit and Loss Questions MAT Probability, Combinatorics Questions MAT Progressions and Series Questions MAT Averages Mixtures Alligations Questions MAT Simple Interest Compound Interest Questions MAT Mensuration Questions MAT Profit And Loss Questions MAT Inequalities Questions MAT Venn Diagrams Questions

MAT DILR Questions | LRDI Questions For MAT

MAT Charts Questions MAT Arrangement Questions MAT Data Interpretation Questions MAT Maxima-Minima Questions MAT Miscellaneous LR Questions MAT Quant Based LR Questions MAT Truth Lie Concept Questions MAT Coins and Weights Questions MAT Special Charts Questions MAT Puzzles Questions MAT Table based DI Sets Questions MAT DI with connected data sets Questions MAT Games and Tournamnents Questions MAT Data Interpretation Basics Questions MAT DI Miscellaneous Questions MAT Data change over a period Questions MAT Venn Diagrams Questions MAT Selection With Condition Questions MAT 2D & 3D LR Questions MAT Scheduling Questions MAT Routes And Networks Questions MAT Quant Based DI Questions

MAT Verbal Ability Questions | VARC Questions For MAT

MAT Odd One Out Questions MAT Para Jumbles Questions MAT Grammar and Sentence Correction Questions MAT Vocabulary Questions MAT Verbal Ability Questions MAT Para Summary Questions MAT Miscellaneous Questions MAT Reading Comprehension Questions MAT Critical Reasoning Questions