In a triangle ABC, let D be the mid-point of BC, and AM be the altitude on BC. If the lengths of AB, BC and CA are in the ratio of 2:4:3, then the ratio of the lengths of BM and AD would be
Solution
We can draw a figure like this:
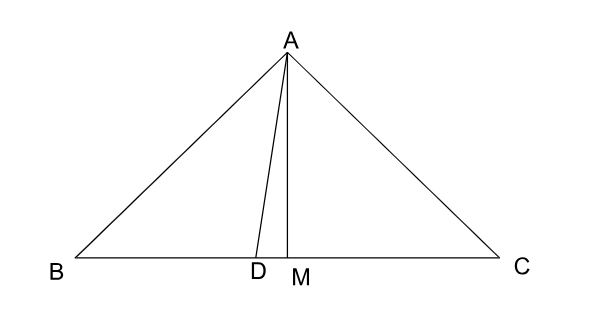
Let us consider the lengths of AB,BC and CA be 2 units, 4 units and 3 units respectively.
As D is the mid point of BC, AD is the median. Also, BD=CD= 2 units.
Using Apollonius theorem,
$$AB^2+AC^2=2\left(AD^2+BD^2\right)$$
or, $$2^2+3^2=2\left(AD^2+2^2\right)$$
or, $$AD^2=\dfrac{5}{2}$$
or, $$AD=\dfrac{\sqrt{\ 10}}{2}$$ ------>(1)
Now, $$AM$$ is perpendicular to $$BC$$.
So, $$\triangle\ AMB$$ and $$\triangle\ AMC$$ both are right angled triangles.
Using Pythagoras theorem in $$\triangle\ AMB$$, we can write,
$$AM^2=AB^2-BM^2$$
or, $$AM^2=2^2-BM^2$$ ----->(2)
Similarly, using Pythagoras theorem in $$\triangle\ AMC$$, we can write,
$$AM^2=AC^2-CM^2$$
or, $$AM^2=3^2-\left(4-BM\right)^2$$ ------->(3)
From equation (2) and (3),
$$3^2-\left(4-BM\right)^2=2^2-BM^2$$
or, $$3^2-2^2=\left(4-BM\right)^2-BM^2$$
or, $$5=\left(4-2BM\right)\cdot4$$
or, $$BM=\dfrac{11}{8}$$ ----->(4)
From equation (1) and (4),
$$\dfrac{BM}{AD}=\dfrac{\dfrac{11}{8}}{\dfrac{\sqrt{\ 10}}{2}}=\dfrac{11}{4\sqrt{\ 10}}$$
So, $$BM:AD=11:4\sqrt{\ 2}$$
Create a FREE account and get:
- Download Maths Shortcuts PDF
- Get 300+ previous papers with solutions PDF
- 500+ Online Tests for Free

