In a city, 50% of the population can speak in exactly one language among Hindi, English and Tamil, while 40% of the population can speak in at least two of these three languages. Moreover, the number of people who cannot speak in any of these three languages is twice the number of people who can speak in all these three languages. If 52% of the population can speak in Hindi and 25% of the population can speak exactly in one language among English and Tamil, then the percentage of the population who can speak in Hindi and in exactly one more language among English and Tamil is _______________.
Solution
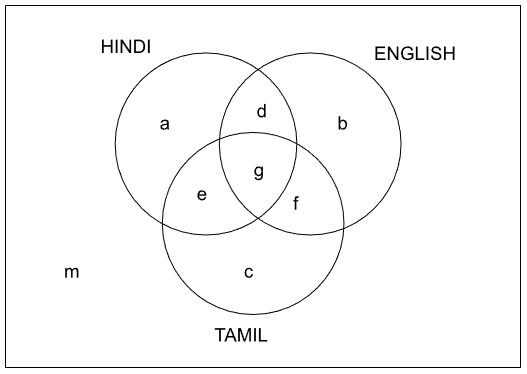
Let's say there are 100 people in the town. 50% of the population can speak in exactly one language among Hindi, English and Tamil.
=> a + b + c = 50
40% of the population can speak in at least two of the three languages
=> d + e + f + g = 40
Now, a + b + c + d + e + f + g + m = 100
=> 50 + 40 + m = 100
=> m = 10
The number of people who cannot speak in any of these three languages is twice the number of people who can speak in all three languages.
=> m = 2g => 10 = 2g => g = 5.
25% of the population can speak exactly in one language among English and Tamil
=> b + c = 25
This means that a = 25 as well because a + b + c = 50.
52% of the population can speak Hindi
=> a + d + c + g = 52
=> 25 + d + c + 5 = 52
=> d + c = 22
Therefore, the percentage of the population who can speak Hindi and exactly one more language, among English and Tamil (that is, d + c), is 22%.
Create a FREE account and get:
- Download Maths Shortcuts PDF
- Get 300+ previous papers with solutions PDF
- 500+ Online Tests for Free

