A person standing at the center of an open ground first walks 32 meters towards the east, takes a right turn and walks 16 meters, takes another right turn and walks 8 meters, and so on. How far will the person be from the original starting point after an infinite number of such walks in this pattern?
Solution
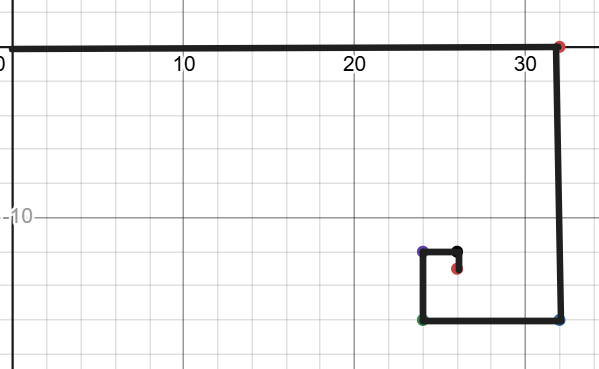
Let's draw the point on the coordinate axis. For the first point, we would go +32 on the x-axis. For the second point, we will go -16 on y asix.
For the third point, we go -8 on the x-axis. And for the next point, we go +4 on the y-axis. For the next one, we go +2 on the x-axis, and for the next one, we go -1 on the y-axis. For the next point, we go -1/2 on the x-axis, and for the next one, we go +1/4 on the y-axis.
Let's observe the moment wrt the x-axis.
+32, -8, +2, -1/2 ...
This is a G.P series with -1/4 as the standard ratio.
The final point's x coordinate will be the sum of all the moments with respect to the x-axis.
Sum to infinite terms of GP = $$\frac{a}{1-r}=\frac{32}{1-\left(-\frac{1}{4}\right)}=\frac{32}{\frac{5}{4}}=\frac{128}{5}$$
Similarly, let's see the moment wrt the y-axis.
-16, +4, -1, +1/4
This is a G.P series with -1/4 as the standard ratio.
The final point's y coordinate will be the sum of all the moments with respect to the y-axis.
Sum to infinite terms of GP = $$\frac{a}{1-r}=\frac{-16}{1-\left(-\frac{1}{4}\right)}=\frac{-16}{\frac{5}{4}}=\frac{-64}{5}$$
The distance from the origin to this point = $$\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}$$ = $$\sqrt{\left(\frac{128}{5}-0\right)^2+\left(-\frac{64}{5}-0\right)^2}=\sqrt{\left(\frac{128}{5}\right)^2+\left(\frac{64}{5}\right)^2}$$
$$\sqrt{\left(\frac{64}{5}\right)^2\left(2^2+1^2\right)}=\sqrt{\left(\frac{64}{5}\right)^2\left(5\right)}$$
= $$\frac{64}{5}\sqrt{5}$$
Create a FREE account and get:
- Download Maths Shortcuts PDF
- Get 300+ previous papers with solutions PDF
- 500+ Online Tests for Free

