The equation of the straight line passing through the point M (-5,4), such that the portion of it between the axes is divided by the point M into two halves, is

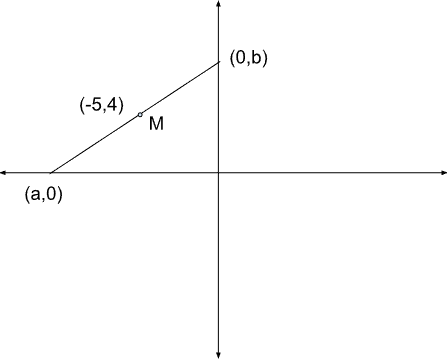
The straight line passing through the point M (-5,4), and the portion of it between the axes is divided by the point M into two halves. This means that M is the midpoint of the line segment joining the intercepts of X-axis and Y-axis

=> $$\dfrac{a+0}{2}=-5$$ => $$a=-10$$

=> $$\dfrac{0+b}{2}=4$$ => $$b=8$$

To get the equation of the line, we will use the line-intercept form.

=> $$\dfrac{x}{a}+\dfrac{y}{b}=1$$

=> $$\dfrac{x}{-10}+\dfrac{y}{8}=1$$

=> $$10y-8x=80$$

ALTERNATE SOLUTION

Check in which of the following equations the point (-5,4) lies on the line by putting the x-coordinate as -5, and the y-coordinate as 4. There is only one equation that will satisfy this condition.