In the xy-plane let A = (-2,0), B = (2,0). Define the set S as the collection of all points C on the circle $$x^{2} + y^{2} = 4$$ such that the area of the triangle ABC is an integer. The number of points in the set S is ___________.
Correct Answer: 14
Solution
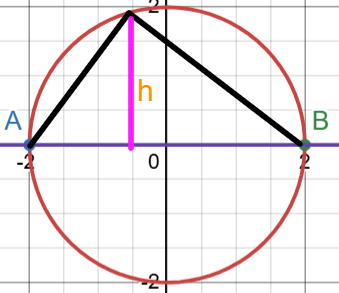
Here, one side of the triangle is the diameter. We know that the third point is on the circle.
So, the triangle is right-angled. AB = 4 units
The area of the triangle will be $$\frac{1}{2}\cdot4\cdot h$$ $$=2h$$
Hence, the area will be an integer when h is an integer and also when h is in the form x.5
The number of such points on a circle is h = 2, 1.5, 1, 0,5. The same heights are possible in four quadrants. 4*4 = 16
However, height 2 is possible once in Q1 and Q2 and once in Q3 and Q4. So, we have to subtract two from 16.
16-2 = 14.
Create a FREE account and get:
- Download Maths Shortcuts PDF
- Get 300+ previous papers with solutions PDF
- 500+ Online Tests for Free

