SSC CGL 24th August 2021 Shift-1

If $$a^4 + b^4 + a^2b^2 = 273$$ and $$a^2 + b^2 - ab = 21$$, then one of the values of $$\left(\frac{1}{a} + \frac{1}{b}\right)$$ is:

A train covers 450 km at a uniform speed. If the speed had been 5 km/h more, it would have taken 1 hour less to cover the same distance. How much time will it take to cover 315 km at its usual speed?

If selling price of 75 articles is equal to cost price of 60 articles, then the approximate loss or gain percent is:

If p is the third proportional to 3, 9, then what is the fourth proportional to 6, p, 4?

Let $$\triangle$$ABC $$\sim$$ $$\triangle$$RPQ and $$\frac{ar(\triangle \text{ABC})}{ar(\triangle \text{PQR})}=\frac{16}{25}$$. If PQ = 4 cm, QR = 6 cm and PR = 7 cm, then AC (in cm) is equal to:

Study the following table and answer the question:
Number of students Appeared (A) and Passed (P) in an annual examination from four schools Q, R, S & T in five years (2014 to 2018)

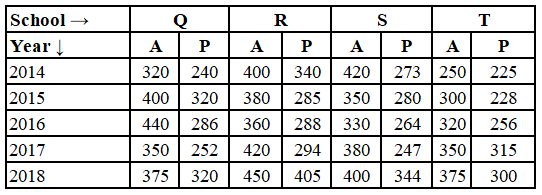
The total number of students passed from school S in 2014 and 2017 is what percent of 90% of the total number of students appeared from school T in 2015, 2016 and 2017? (correct to one decimal place)

The sum of 3-digit numbers abc, cab and bca is not divisible by:

A customer wanted to purchase an item marked for ₹10000. Shopkeeper offered two types of discounts, 25% flat discount or successive discounts of 14% and 12%. Which is the better offer for the customers and by how much?

If $$\tan \theta + 3 \cot \theta - 2\sqrt{3} = 0, 0^\circ < \theta < 90^\circ$$, then what is the value of $$(\cosec^2 \theta + \cos^2 \theta)?$$

ABCD is a cyclic quadrilateral such that when sides AB and DC are produced, they meet at E, and sides AD and BC meet at F, when produced. If $$\angle$$ADE = 80$$^\circ$$ and $$\angle$$AED = 50$$^\circ$$, then what is the measure of $$\angle$$AFB?