SSC CGL 16th August 2021 Shift-2
For the following questions answer them individually
If $$4x^4 - 37x^2 + 9 =0, x > \sqrt{\frac{3}{2}}$$, then what is the value of $$8x^3 - \frac{27}{x^3}$$?
If $$a - \frac{12}{a} = 1$$, where a > 0, then the value of $$a^2 + \frac{16}{a^2}$$ is:
Table shows income (in ₹) received by 4 employees of a company during the month of December 2020 and all their income sources.
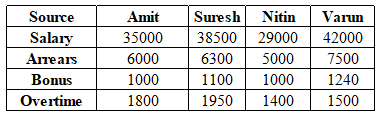
By what percent is the bonus of Varun less than the bonus of Amit and Nitin taken together?
The bar graph shows the number of students enrolled for a science course in institutes A and B during 5 years from 2014 to 2018
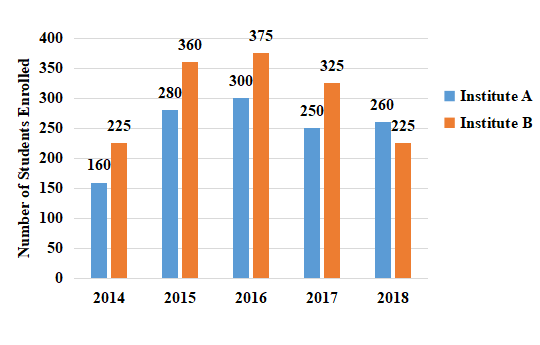
What is the ratio of the total numbers of students enrolled in institute B in 2015 and 2017 to that of students enrolled in institute A in 2014 and 2016?
A train leaves station A at 8 am and reaches station B at 12 noon. A car leaves station B at 8:30 am and reaches station A at the same time when the train reaches station B. At what time do they meet?
The value of $$3\frac{5}{6} + \left[3\frac{2}{3} + \left\{\frac{15}{4}\left(5\frac{4}{5} \div 14\frac{1}{2}\right)\right\}\right]$$ is equal to:
In $$\triangle ABC, AB = 20$$ cm, BC = 21 cm and AC = 29 cm. What is the value of $$\cot C + \cosec C - 2 \tan A$$?
In a triangle ABC, point D lies on AB, and points E and F lie on BC suchthat DF is parallel to AC and DE is parallel to AF. If BE = 4 cm, CF = 3 cm, then find the length (in cm) of EF.
A and B can complete a work in 15 days and 10 days respectively. They started doing the work together but after 4 days B had to leave. Then A working with a new worker C completed the remaining work in 3 days. If C works alone, in how many days he can do 40% of the same work?
If one of the angles of a triangle is $$74^\circ$$, then the angle between the bisectors of the other two interior angles is:
