Question 29
ABC is right angled triangle at C. Let BC = a, CA = b and AB = c and let p be the length of perpendicular from C on AB, then cp is equal to
Solution
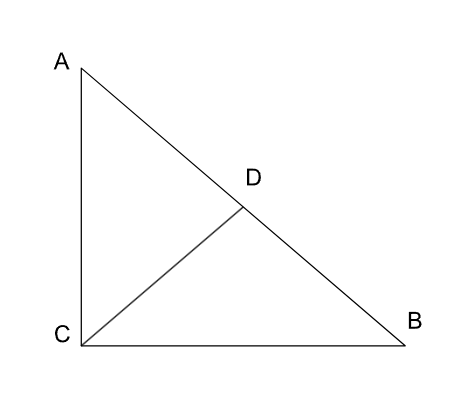
Given that BC = a, AB = c, AC = b, CD = p
CD is perpendicular to AB & <ACB = 90 degrees.
Let <DBC = <ABC = $$\theta\ $$
$$Sin\ \theta\ =\dfrac{\ CD}{CB}=\dfrac{\ AC}{AB}$$
= $$\dfrac{\ p}{a}=\dfrac{\ b}{c}$$
Therefore, pc = ab.
MAT Quant Questions | MAT Quantitative Ability
MAT Number Systems QuestionsMAT Time Speed Distance QuestionsMAT Profit and Loss QuestionsMAT Averages, Ratio and Proportion QuestionsMAT Quadratic Equations QuestionsMAT Profit And Loss QuestionsMAT Linear Equations QuestionsMAT Simple Interest Compound Interest QuestionsMAT Averages QuestionsMAT Logarithms QuestionsMAT Averages Mixtures Alligations QuestionsMAT Remainders QuestionsMAT Coordinate Geometry QuestionsMAT Functions, Graphs and Statistics QuestionsMAT Venn Diagrams QuestionsMAT Probability, Combinatorics QuestionsMAT Arithmetic QuestionsMAT Percentages QuestionsMAT Time, Speed and Distance QuestionsMAT Geometry QuestionsMAT Number Series QuestionsMAT Progressions and Series QuestionsMAT Inequalities QuestionsMAT Logarithms, Surds and Indices QuestionsMAT Time And Work QuestionsMAT Data Sufficiency QuestionsMAT Mensuration QuestionsMAT Algebra Questions
MAT DILR Questions | LRDI Questions For MAT
MAT Venn Diagrams QuestionsMAT Truth Lie Concept QuestionsMAT Special Charts QuestionsMAT Miscellaneous LR QuestionsMAT Arrangement QuestionsMAT Selection With Condition QuestionsMAT 2D & 3D LR QuestionsMAT Coins and Weights QuestionsMAT Scheduling QuestionsMAT Quant Based LR QuestionsMAT Games and Tournamnents QuestionsMAT DI Miscellaneous QuestionsMAT Puzzles QuestionsMAT Charts QuestionsMAT Routes And Networks QuestionsMAT Maxima-Minima QuestionsMAT Quant Based DI QuestionsMAT Data Interpretation Basics QuestionsMAT Table based DI Sets QuestionsMAT DI with connected data sets QuestionsMAT Data Interpretation QuestionsMAT Data change over a period Questions
