The radius of two concentric circles are 13 cm and 8 cm. AB is a diameter of the bigger circle. BD is tangent to the smaller circle touching it at D. The length AD is.
Solution
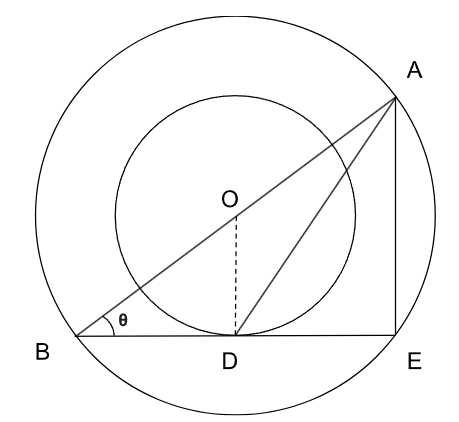
As BD is a tangent , we can say OD is perpendicular to BE i.e <ODB = 90
$$Sin\ \theta\ =\dfrac{\ OD}{OB}=\dfrac{\ 8}{13}$$
<BOD = $$90-\theta\ $$
Since, <BOD + <DOA = 180 degrees
this can imply us that <DOA = 180 - ($$90-\theta\ $$)
= $$90+\theta\ $$
In triangle DOA, by applying cosine rule formula :
cos ($$90+\theta\ $$) = $$\ \dfrac{\ OA^2+OD^2-AD^2}{2\left(OA\right)\left(OD\right)}$$
$$-\sin\theta\ $$ = $$\dfrac{\ 13^2+8^2-AD^2}{2\left(13\right)\left(8\right)}$$
$$\dfrac{\ -8}{13}$$ = $$\dfrac{\ 13^2+8^2-AD^2}{2\left(13\right)\left(8\right)}$$
Therefore, AD = 19.