Cost price of article A is ₹ 200 more than the cost price of article B. Article A was sold at 10% loss and article B was sold at 25% profit. If the overall profit earned after selling both the articles is 4%, then what is the cost price of article B?
Solution
Let, cost price of article B be ₹ x
So, cost price of article A = ₹ (x+200)
So, selling price of article A = ₹ $$(x+200)\times\ 0.9=0.9x+180$$
Selling price of article B = ₹ $$1.25x$$
So, total selling price = ₹($$1.25x+0.9x+180$$) = ₹($$2.15x+180$$)
Also, overall profit = 4%
So we can say, ($$2.15x+180$$) = $$1.04\left(x+x+200\right)$$
or, $$2.15x+180=2.08x+208$$
or, $$2.15x-2.08x=208-180$$
or, $$0.07x=28$$
or, $$x=\dfrac{28}{0.07}=400$$
So, cost price of article B = ₹400
Video Solution
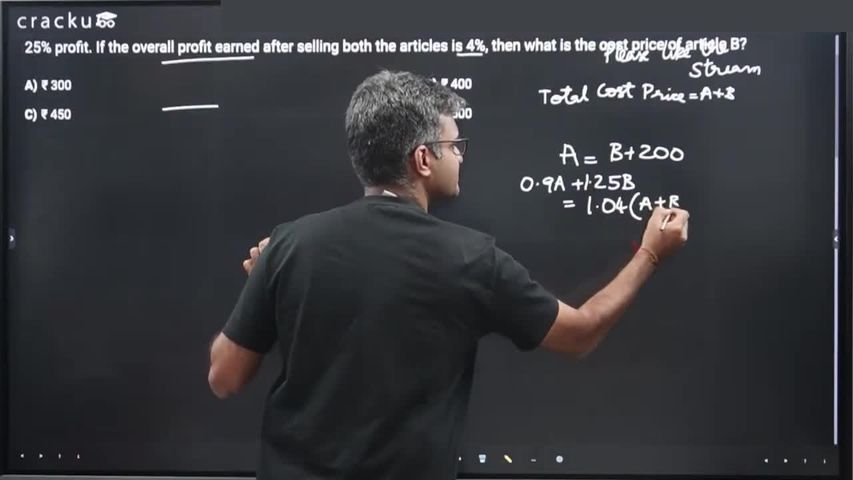
Click on the Email ☝️ to Watch the Video Solution