If the seven digit number 94a29b6 is divisible by 72 , then what is the value of (2a + 3b) for a $$\neq$$ b ?
Solution
We know that $$72=8\times9$$. Thus, for any number to be divisible by 72, the number should be divisible by both 8 and 9.
For the number to be divisible by 8, the last three digits of the number should be divisible by 8.
Thus, 9b6 should be divisible by 8. Therefore, the value of b can be either 3 or 7.
For the number to be divisible by 9, the sum of digits of the number should be divisible by 9.
Thus, (30 + a + b) should be divisible by 9. Therefore, a+b can be either 6 or 15.
Case 1: (a + b) = 6
In this case, b cannot be 7, because both a and b are single digit integers. Thus, b = 3. But, then a = 3 as well, and it is given that a is not equal to b. Thus, this case can never be true.
Case 2: (a + b) = 15
In this case, b cannot be 3, because both a and b are single digit integers. Thus, b = 7. But, then a = 8.
Thus, the value of $$2a+3b=2(8)+3(7)=16+21=37$$.
Video Solution
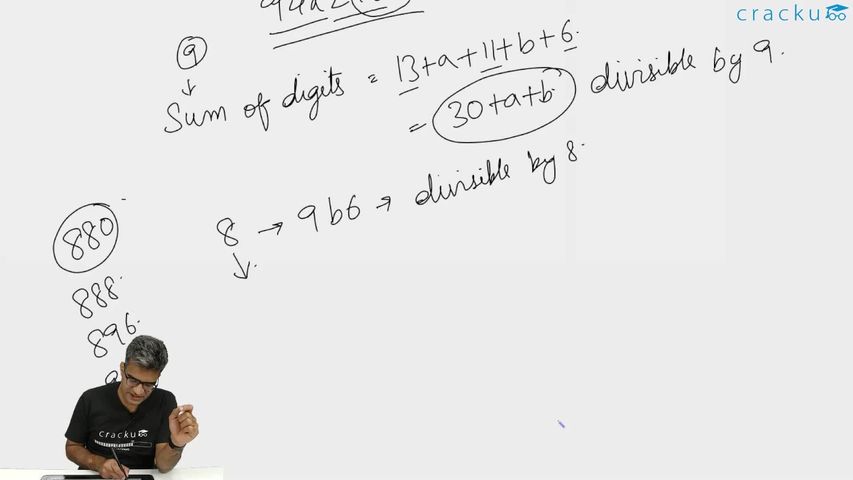
Click on the Email ☝️ to Watch the Video Solution