JIPMAT 2022 Question Paper
For the following questions answer them individually
JIPMAT 2022 - Question 21
Three years ago, the ratio of ages of Amisha and Namisha was 8:9. Three years from now the ratio will become 11:12. What is the present age of Amisha?
JIPMAT 2022 - Question 22
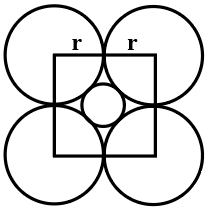
If the radius of each of four outer circles is $$r$$, then the radius of the innermost circle is
JIPMAT 2022 - Question 23
If $$\sin(\alpha)$$ and $$\cos(\alpha)$$ are the roots of the equation $$ax^{2}+bx+c=0$$, then $$b^{2}$$ is
JIPMAT 2022 - Question 24
If the mean of a, b and c is $$M$$; ab + bc + ca = 0; and the mean of $$a^{2}$$, $$b^{2}$$ and $$c^{2}$$ is $$KM^{2}$$ then $$K$$ is equal to
JIPMAT 2022 - Question 25

Match List I with List II. Choose the correct answer from the options given below:
JIPMAT 2022 - Question 26
$$\dfrac{\sqrt{5}+\sqrt{3}}{\sqrt{8-2\sqrt{15}}}+\dfrac{\sqrt{11+2\sqrt{30}}}{\sqrt{6}-\sqrt{5}}$$
JIPMAT 2022 - Question 27
If $$a\times b=2a- 3b+ab$$, then $$3\times 5+5\times 3$$ is equal to
JIPMAT 2022 - Question 28
The value of $$\dfrac{325\times 325 \times 325 + 175 +175 +175}{325\times 325 -325 \times 175+175 \times 175}$$ is
JIPMAT 2022 - Question 29
Given below are two statements:
Statement I: In $$\triangle ABC$$, $$AB=6\sqrt{3}cm$$, $$AC=12cm$$ and $$BC=6cm$$, then angle $$B=90^{o}$$
Statement II: In $$\triangle ABC$$, is an isosceles with $$AC = BC$$. If $$AB^{2}= 2AC^{2}$$, Thenangle $$C=90^{o}$$
In the light of the above statement, choose the correct answer form the question below.
JIPMAT 2022 - Question 30
Given below are two statements:
Statement I: If $$sin(\theta) =\dfrac{5}{13}$$, then the value of $$tan(\theta)=\dfrac{5}{12}$$
Statement II: If $$cot(\theta) =\dfrac{12}{5}$$, then the value of $$sin(\theta)=\dfrac{5}{12}$$
