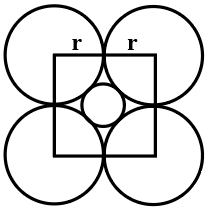
If the radius of each of four outer circles is $$r$$, then the radius of the innermost circle is

Let the radius of the inner circle be x. If we join the four centres of the outer circle, then it will be a square as the radius of each circle is equal, thus, the side length of the square will be 2r. 

Now, the innermost circle is touching all four circles and the radius of all the circles is equal, thus the length of the line joining the diagonally opposite points will be = (r + x + x + r) = (2r + 2x)

Also, the length of the diagonal is $$\sqrt{\left(2r\right)^2+\left(2r\right)^2}=2\sqrt{2}r$$

Therefore - 

$$2r+2x=2\sqrt{2}r$$

$$x=\left(\sqrt{2}-1\right)r$$