Question 8
The HCF and LCM of two numbers x and y are respectively 6 and 210.
If x + y = 72, then $$\frac{1}{x}+\frac{1}{y}$$ is equal to.
Solution
The HCF and LCM of two numbers x and y are respectively 6 and 210.
$$x\times y=HCF\times LCM$$
$$xy=1260$$
$$x=\dfrac{1260}{y}$$
It is given that $$x+y=72$$
$$y+\dfrac{1260}{y}=72$$
$$y^2-72y+1260=0$$
$$y^2-42y-30y+1260=0$$
Thus, y = 42 or 30. Then, x = 30 or 42.
$$\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{42}+\dfrac{1}{30}=\dfrac{7+5}{210}=\dfrac{2}{35}$$
Get AI Help?
Video Solution
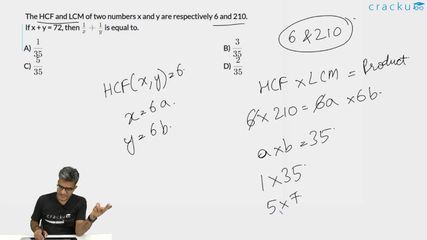
Click on the Email ☝️ to Watch the Video Solution
