Question 33
If $$2^{x}=3^{y}=6^{-z}$$, then $$\left( \frac{1}{x} + \frac{1}{y} + \frac{1}{z}\right)$$ is equal to
Solution
$$2^{x}=3^{y}=6^{-z}$$ = K
X = $$\log_2k$$
Y = $$\log_3k$$
Z = -($$\log_6k$$)
Hence, $$\left( \frac{1}{x} + \frac{1}{y} + \frac{1}{z}\right)$$ = $$\log_k2$$ + $$\log_k3$$ - $$\log_k6$$
= $$\log_k6$$ - $$\log_k6$$
= 0.
Video Solution
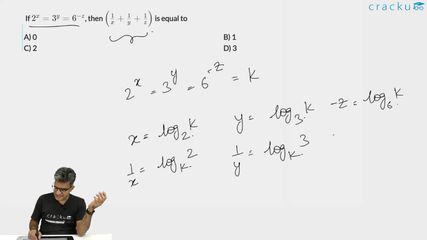
Click on the Email ☝️ to Watch the Video Solution