In $$\triangle ABC,\angle B = 90^{o}, BC = 5 cm, AC - AB =1 cm$$, then $$\frac{1 + \sin(C)}{1 + \cos(C)}$$ is

In a right angled triangle ABC with right angle at B : $$AB^2+BC^2=AC^2$$.

given, BC = 5 , (AC-AB) = 1 .
    Hence, we can write :  $$AB^2+5^2=(1+AB)^2$$
                                         24 = 2 (AB)
    so, AB = 12 cm.

AC = 1 + AB = 13 cm. 
BC = $$\sqrt{13^2-12^2}=\ 5$$

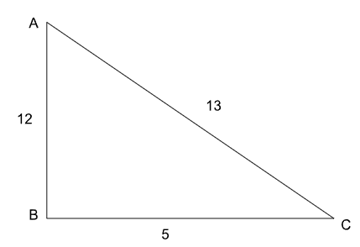
Hence, Sin(C) = $$\dfrac{\ AB}{AC}$$ = $$\dfrac{\ 12}{13}$$
           
           Cos(C) = $$\dfrac{\ BC}{AC}$$ = $$\dfrac{\ 5}{13}$$     

Therefore, $$\dfrac{1 + \sin(C)}{1 + \cos(C)}$$ = $$\dfrac{25}{18}$$ .