Top 50 Quant Questions for XAT 2023 – Download PDF
Download Top-50 XAT Quant Questions pdf by Cracku. Top 50 very Important Quant Questions for XAT based on asked questions in previous exam papers. These questions will help you in quant preparation. So kindly download the PDF for refrence and do practice more.
Download Top 50 Quant Questions for XAT PDF
Question 1: A machine takes the last 2 digits of a number expressed in the form of $a^b$ and flips the digits. Which amongst the following will result in the biggest number as the output?
a) $23^{25}$
b) $25^{12}$
c) $11^{11}$
d) $13^{25}$
Question 2: A number ‘n’ can be written as “$abc$” in base 14 whereas we write the same number as “$acb$” in base 15. If the same number can be written as “$acac$”(a $\neq$ 0) in base 6, then find out the sum of digits of the number ‘n’ in base 10 representation.
a) 14
b) 16
c) 18
d) 20
e) None of these
Question 3: Find the number of factors of 8690220 which are also a multiple of 209.
Question 4: HCF and LCM of two numbers, A and B, are 7 and 315 respectively. Find the number of possible order pairs of (A, B)?
a) 2
b) 4
c) 6
d) 3
Question 5: If x-y-z=20 and x $\leq$ 30,y $\leq$ 7 and z $\leq$ 8 and x,y,z are positive integers.Then the number of integral solutions (x,y,z) is
a) Infinite
b) 40
c) 45
d) 41
Question 6: For the inequality (x-10)(x-12)(x-14)…(x-98) < 0, how many different positive integral values of x are possible?
Question 7: What is the number of distinct quadratic equations having real roots that can be formed such that $ax^2 + bx – 4 = 0$, if $a$ and $b$ $\in$ {-5, -3, -1, 0, 1, 5}
Question 8: Find the sum of all positive values of x, where $\dfrac{1}{x^2 – 3x -18} + \dfrac{1}{x^2 – 3x -34} – \dfrac{2}{x^2 – 3x – 58} = 0$
Question 9: If $x$ and $y$ are two positive integers such that $x^2+44x+656 = y^2$, what is the sum of all possible values of $x+y$?
a) 64
b) 176
c) 92
d) 136
Question 10: What is the total number of solution sets (x,y) of the equation $5x^2 – 4xy + 2y^2 – 3 = 2(x + 2y)$ such that both x and y are non-negative integers?
Coordinate Geometry Questions For XAT
Question 11: Find the sum of positive integral values of $x$ less than 20 such that $\dfrac{1}{x^2-18x-16} \leq \dfrac{5}{2}$
Question 12: Ramesh, a shopkeeper, mixes 3 varieties of rice costing Rs. 20/kg, Rs. 17/kg, and Rs. 18/kg in the ratio a:b:c respectively. b is the geometric mean of a and c and a is less than c. He marks up the price of the mixture by 66.67% and then provides a discount of 20%, earning a profit of Rs.6 on every kg of the mixture sold. One day, by mistake, Ramesh mixes the 3 varieties of rice in the ratio c:a:b (instead of a:b:c) and sells the mixture at the usual selling price. What is the profit per kg of the mixture sold?
Question 13: Rinesh arranged numbers in a grid with ‘n’ rows and 10 columns. He wrote five consecutive natural numbers in each row. The odd rows had numbers in the odd columns and the even rows had numbers in the even columns. Furthermore, the numbers in the odd rows were in ascending order while the numbers in the even rows were in descending order.The first row had the first five natural numbers, the second row had the next five natural numbers and so on. If 752 is in $P^{th}$ row and $A^{th}$ column and 1244 is in $Q^{th}$ row and $B^{th}$ column. Find the ratio of $\frac{P+Q}{A+B}$
Question 14: A shopkeeper sells an article at a profit of $x$%. The person who buys the article sells it to his friend at a loss of $x$%. The friend compares the prices and realizes that he has obtained the article for $\frac{x}{4}$ % less than the cost price of the article. If the friend obtained the article for Rs.100 less than the cost price of the article, then the loss borne by the person who sold it to his friend (in rupees) is
Question 15: Peter divided some amount of money among his two sons and two daughters in the ratio $\dfrac{1}{9} :\dfrac{1}{17} : \dfrac{1}{11} : \dfrac{1}{13}$. If the difference between the highest amount and the lowest amount is Rs. 5720, what is the total amount distributed?
Question 16: A travel company rents out buses and charges on the basis of distance as well as the number of passengers on a trip. It was found out that the profit was directly proportional to the distance travelled and the square of number of passengers. The ratio of the average profit (profit earned per passenger) when a bus was rented by 30 passengers for 50 kms to a bus for 150 kms carrying $\frac{1}{2}$ the number of passengers was 2:3. If the lesser of the two overall profits earned ₹45000 for the company, find the difference in profit when 15 people go for a trip 200 kms away and when 20 people go for a trip 300 kms away.
a) ₹80,000
b) ₹90,000
c) ₹1,00,000
d) ₹85,000
Question 17: The water tank of a house is in the shape of an inverted cone. The height of the conical tank is 10 metres and the area of it’s base is 9R. The water tank has an outlet pipe at a height of 5 metres. The owner fills the tank every morning in 10 hours via an inlet pipe located at the bottom tip of the inverted cone. If one morning, the owner forgets to close the outlet, how much time will it take in hours to fill the empty tank completely. Given, the ratio of efficiencies of the inlet and the outlet pipes is 2:1.
a) 18.75 hours
b) 14 hours
c) 16.25 hours
d) 17.75 hours
Question 18: Golu, a 5-year old kid, walks up an escalator that is moving downwards. After this he walks up another escalator of the same length moving upwards. Both these escalators have the same speed. The ratio of the time taken by Golu on the first escalator to that on the second is 9:4 and the total time spent on both escalators is 208 seconds.
How much time would Golu take to go down an upwards moving escalator if this escalator has the same length as the first two escalators but runs at half the speed of the first two escalators?
a) 110 seconds
b) 102 seconds
c) 115 seconds
d) 109 seconds
Question 19: X and Y are two cruises travelling between Goa and Mumbai. X starts its journey at 9:00 pm from Mumbai to Goa on Sunday while Y starts its journey from Goa to Mumbai at 5:00 am on Monday. They both meet at 6:00 am. The distance travelled by both the cruises is in the ratio 4:1. It is known that the distance between Goa and Mumbai is 1000 kms. Find the headstart (in kms) that needs to be given to the slower cruise from Goa in order to ensure that both the cruises reach Mumbai simultaneously.
a) 564.88 kms
b) 510.22 kms
c) 555.55 kms
d) 495.66 kms
Question 20: A tank is cylindrical in shape with 2 identical outlets pipes located : one at $(\frac{3}{10})^{th}$ its height from the bottom of the tank and another in the bottom. The difference between time taken to empty a full tank and a $(\frac{8}{10})^{th}$ full tank is 10 hours. How long will it take to fill the empty tank if 4 inlet pipes, each double the capacity of the outlet pipes are installed and the outlet pipes also work simultaneously (approx)?
a) 25
b) 16
c) 10
d) 20
Data Interpretation Questions For XAT Preparation
Question 21: Three men A,B and C are hired to do some construction work. The work involves making the foundation of building X and some work on walls of building Y. Of the three, only A and B have the skills to do the work of the foundation. C can work only on the walls of building Y. A and B can finish the work of the foundation alone in 8 days each. For the work of the walls, A,B,C take 10,8,6 days respectively to finish the work alone respectively. A and B finished the work on building X together and then helped C finish the work on building Y. If the client paid ₹10,000 and ₹18,000 for the work on building X and building Y respectively along with daily wages of ₹500/worker/day, how much did B earn (approx) ? (assume that the client pays everyone for a full day’s work even if they do not work the whole day)
a) ₹ 9,415
b) ₹ 10,595
c) ₹ 8,465
d) ₹ 9,500
Question 22: There is a hexagonal path having a side of length $\dfrac{7}{\sqrt{3}}$m. There is a circular path inside this hexagonal path such that it touches the hexagonal path at exactly 6 places. Amit and Baldev decide to run a race from the same point in the same direction. Amit will run along the hexagonal path and Baldev will run along the circular path. The speed of Amit is $2\sqrt{3}$m/s and speed of Baldev is 2m/s. If both of them finish at the same time, then how much time after Baldev started running did Amit start running? (Enter your answer in the box provided in seconds)
Assume that $\pi = \frac{22}{7}$
Question 23: Aman, Bhushan, and Chintu decide to go to Goa via train. They decide to meet at Aman’s house and then go to the railway station in a car. The railway station is situated at a distance of 36 Km from Aman’s house. On the day of the journey, they found out that the car has a flat tire and hence, they decide to go to the station on a bike. Since a bike can carry only 2 persons at a time, they decide that 2 of them will leave the house on the bike and the third person will walk. After dropping 1 person at the station, the other person will return and pick up the 3rd person. If the speed of the bike is 48 km/hr and Aman, Bhushan, and Chintu can walk at a speed of 4, 6 and 8 km/hr respectively, then what will be the minimum time required for all of them to reach the station?
a) 1.82 hours
b) 2.21 hours
c) 2 hours
d) 1.666 hours
Question 24: There are 2 escalators, each of 200 steps, running parallel to each other. One is going up and the other is going down. Natwarlal, a thief, is going up the escalator which is going up (i.e, the escalator is going up and Natwarlal is going up relative to the escalator) and Niharilal, a policeman, is going down the escalator which is going down (i.e, the escalator is going down and Niharilal is going down relative to the escalator). When both Natwarlal and Niharilal were in the middle of the escalator, Niharilal recognizes Natwarlal and changes his direction and starts moving up to catch Natwarlal. Natwarlal reaches the top of the escalator in 20s after being recognized and starts running at the same speed. Niharilal after reaching the top of the escalator starts running behind Natwarlal at the same speed. If he was able to catch Natwarlal in a total of 80 seconds (after spotting Natwarlal on the escalator) , then what is the ratio of the speeds of Natwarlal and Niharilal?(speed of escalator = 2 steps/ second and 1 step is 1m)
a) 3:1
b) 2:3
c) 1:2
d) Either a or b
Question 25: A whole-seller sells apples to a fruit vendor at cost price. The vendor manages to trick the whole-seller into giving him an extra apple per four apples that he buys and manages to get a total of 200 apples. But, the whole-seller on sensing some foul play decides to change the weighing machine, citing some fault in it, for measuring the remaining of the total number of apples sold. The new weighing machine is such that it shows the weight of 3 apples equivalent to 5 apples.( For this transaction, the vendor does not trick the wholesaler). How much does the whole-seller gain/lose in the entire transaction if a total of 600 apples were sold? (Assume all apples to be of uniform size and weight)
a) Loss of 33.33%
b) Gain of 33.33%
c) Loss of 37.78%
d) Gain of 37.78%
Number System Questions For XAT Preparation
Question 26: A shopkeeper marks up the price of a mobile phone by 14.28%. The percent of discount he offered on the mobile, and the profit/loss he incurred on it is in the ratio of 4: 5. Find his profit or loss percentage.
a) 7.46% loss
b) 7.14 % profit
c) 7.14 % loss
d) 7.46% profit
Question 27: If $b=[log_{5}{a}]^3 + 12*[log_{5}{a}] – 6 * [log_{5}{a}]^2 – 8 $ and $a^b = 125$. If $a$ and $b$ are positive numbers, what is the value of $log_{5}{b}$?
Question 28: The sum of all the terms in the expansion of $(\sqrt[8]{x} + \sqrt[6]{y})^{72}$ which have integral powers of both x and y is always divisible by
a) $x^3 y^4$
b) $(x^3 +y^4)^3$
c) $(x^3y^8 + x^6y^4)$
d) None of these
Question 29: The number of digits in $(2401^{35})_7 $ is? (Subscript represents the base in which the number is written)
Question 30: For every value of ‘a’, how many values of b satisfy the equation $log_{b}a+ log_{ab}a^2 + log_{a^{2}b}a^{3} =0$, when $a>1$ and $a \neq b$? (Enter -1, if the answer cannot be determined)
Question 31: The number of triangles with 2 odd and an even integral side that can be formed when the perimeter is 150 is
Question 32: In a shelf, there are books on 8 different subjects, namely Politics, Economics, Psychology, Genetics, Feminism, Linguistics, Sports, Fitness. Each of these subjects were allotted a specific rack in the library. However, the librarian misplaced a few of the subjects and placed only two subjects in its rack. Let X be the number of ways in which this can be done.What is the sum of the digits of X?
Question 33: If the square of a number has 61 factors, how many factors the number will have?Enter -1 if the answer can’t be determined.
Question 34: N is an integer such that 10^6 < N < 10^7 and the sum of the digits = 4. Let M be the number of possible values of N. The factorial of each digit of M is calculated and the sum of the factorials was found to be S. What is the remainder when S is divided by 10?
Question 35: Find the number of points at which at least 2 of the following three functions intersect.
$ x^2 – 6x = 8y – y^2$
$ y = \sqrt{3}x – (6+3\sqrt{3})$
$ y -1 = x – 6\sqrt{2}$
a) 4
b) 5
c) 2
d) 3
Time, Speed, Distance Questions For XAT Preparation
Question 36: k is a natural number where $f(x,k).f(x,k+1) = 1$. What is the value of
|$\sum_{k=5}^{100}[f(x,k.(k+4))*f(x,(k+3).(k+5))]$|
Question 37: Two sheets of paper in shape of equilateral triangles with side $a$ are overlapping over each other completely. One of the sheets is rotated about the axis passing through the centroid and perpendicular to the plane of sheets by $30\small^o$. What is the area of the region that is not overlapped?
a) ${\frac{3\sqrt{3}a^2}{3+2\sqrt{3}}}$
b) ${\frac{\sqrt{3}a^2}{7+4\sqrt{3}}}$
c) ${\frac{\sqrt{3}a^2}{4+2\sqrt{3}}}$
d) ${\frac{3\sqrt{3}a^2}{2+3\sqrt{3}}}$
Question 38: A farmer has a rectangle shaped piece of land with the ratio of length and breadth in the ratio 8:5. He constructed three small rectangles at the corners of the land as shown in the diagram. The ratio of the length and breadth of the smaller rectangles is same as that of the bigger rectangle and the area of each of the smaller rectangle is $(\frac{1}{9})^{th}$ that of the bigger rectangle. In two of them, he planted indigo (coloured blue) while in the space between the three smaller rectangles, he planted wheat as shown in the figure (coloured yellow). What is the ratio of cost incurred on ploughing the wheat field and ploughing the indigo field ? Ploughing the wheat field costs $₹15/m^2$ and ploughing the indigo field costs $₹20/m^2$

a) 9:8
b) 8:7
c) 7:6
d) 6:5
Question 39: ABCD is a square of side 10 units. EFGH is another square made by connecting the midpoints of sides of square ABCD. It is also known that I,J,K,L are midpoints of the line segments AE,FC,GC,AH respectively. If the area of the shaded region is expressed as $\dfrac{m}{n}$ (in the lowest terms) then find the value of m+n.

a) 200
b) 221
c) 229
d) 225
Question 40: Point A is the reflection of the point (1,2) about the line 2x-4y=5 and point B is the reflection of the same point about the line x-y=3. What is the distance between A and B?
a) $\sqrt{4.6}$
b) $2$
c) $\sqrt{3.4}$
d) $4.6$
Percentages & Venn Diagram Questions For XAT Preparation
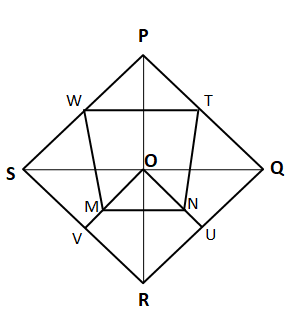
Question 41: In a rhombus PQRS, T, U, V and W are the midpoints of sides PQ, QR, RS and SP respectively. O is the point of intersection of the diagonals of the rhombus. If M and N are the mid points of OV and OU respectively, then find out the ratio of the area of pentagon MNURV to area of quadrilateral WTNM?
a) 7 : 9
b) 2 : 3
c) 5 : 6
d) 8 : 9
Question 42: A rectangle consists of 14 congruent circles as shown in the figure. All of the circles in 1st and 3rd rows are the tangents to at least one side of the rectangle and one circle. While in the 2nd row all the circles are touching at least five circles. If the ratio of the longer side of the rectangle to the shorter side can be written as $\dfrac{1}{2}(\sqrt{A} – {B})$, where A and B are positive integers. Find the value of $\dfrac{A}{B}$.
a) 19
b) 17
c) 15
d) 21
Question 43: An isosceles $\triangle$PQR is drawn such that PQ = PR. It is known to us that the T is the intersection point of the bisectors of $\angle$Q and $\angle$R. If QT = 10 cm and the triangle has positive integer side lengths, then find out the smallest possible perimeter of $\triangle$PQR.
Question 44: A square is formed by lines |x-2| = 3, |y-2| = 3. If a circle of radius 2 units is drawn such that its centre coincides with the centre of the square then find out the number of points with integral coordinates which lie outside the circle but within the square?
Instructions
Read the following caselet and choose the best alternative.
The BIG and Colourful Company
You are running “BIG and Colourful (BnC)” company that sells book to customers through three retail formats:
a. You can buy books from bookstores,
b. You can buy books from supermarket,
c. You can order books over the Internet (Online)
Your manager has an interesting way of classifying expenses: some of the expenses are classified in terms of size: Big, Small and Medium; and others are classified in terms of the colors, Red, Yellow, Green and Violet. The company has a history of categorizing overall costs into initial costs and additional costs. Additional costs are equal to the sum of Big, Small and Medium expenses There are two types of margin, contribution(sales minus initial costs) and profit (contribution minus additional costs). Given in table 1 is the data about sales and costs of BnC.
Each of the Big, Small and Medium cost is categorized by the manager into Red, Yellow, Green and Violet costs. Breakdown of the additional costs under these headings is shown in the table 2 below.
Red, Yellow, Green and Violet costs are allocated to different retail formats. These costs are apportioned in the ratio of number of units consumed by each retail format. The number of units consumed by each retail format is given in the table 3 below.
<img “=”” alt=”” class=”img-responsive” src=”https://cracku.in/media/questionGroup/Screenshot_2014-12-23_17.36.08.png “/>
Question 45: Which retail format gives the highest profit for BnC?
a) Book Store
b) Supermarket
c) Online
d) All are equally profitable
e) Cannot be determined from the given information
Download XAT Previous Papers PDF
Question 46: Based on the previous two questions answer the following question:
Which retail format is least profit making for BnC
a) Online
b) Supermarket
c) Book Store
d) All formats are loss making.
e) All formats are profit making.
Question 47: Based on your answer to the previous question answer the following qn:
What is the profit/loss from “online” sales?
a) 0
b) -310
c) +20
d) +450
e) Cannot be determined from given information
Instructions
The following graphs and tables gives the performance of three companies- X, Y and Z during the period 2005 to 2010

Profit Percentage = $\frac{Income – Expenditure}{Expenditure} \times100$
Question 48: For which of the following companies was the ratio of Income to Expenditure greater than 6/5 but less than 7/5 in exactly two of the six years given?
a) X
b) Y
c) Z
d) Both X and Z
e) Both Y and Z
Question 49: In how many years is the expenditure on raw materials of one or more companies equal to the profit of the company that year?
a) 2
b) 3
c) 4
d) 5
e) 6
Question 50: In which year was the ratio of expenditure of Company X to that of Company Z the highest?
a) 2006
b) 2007
c) 2008
d) 2009
e) 2010
Answers & Solutions:
1) Answer (B)
To find the last 2 digits of a number, we have to find the remainder when the number is divided by 100.
Option A : $R(\dfrac{23^{25}}{100}) $
$ \Rightarrow R(\dfrac{29^{12} \times 23}{100}) $
$ \Rightarrow R(\dfrac{41^{6} \times 23}{100}) $
$ \Rightarrow R(\dfrac{81^{3} \times 23}{100}) $
$ \Rightarrow R(\dfrac{61 \times 81 \times 23}{100}) $
$ \Rightarrow R = 43 $
Output = 34
Option B : $R(\dfrac{25^{12}}{100}) $
$ \Rightarrow R(\dfrac{25^{12}}{100}) $
In case of any number with last two-digits 25, the last 2 digits are always 25.
Thus, output = 52
Option C : $R(\dfrac{11^{11}}{100}) $
$ \Rightarrow R(\dfrac{21^{5} \times 11}{100}) $
$ \Rightarrow R(\dfrac{41^{2} \times 21 \times 11}{100}) $
$ \Rightarrow R(\dfrac{81 \times 31}{100}) $
$ \Rightarrow R = 11 $
Output = 11
Option D : $R(\dfrac{13^{25}}{100}) $
$ \Rightarrow R(\dfrac{69^{12} \times 13}{100}) $
$ \Rightarrow R(\dfrac{61^{6} \times 13}{100}) $
$ \Rightarrow R(\dfrac{21^{3} \times 13}{100}) $
$ \Rightarrow R(\dfrac{61 \times 13}{100}) $
$ \Rightarrow R = 93 $
Output = 39
Hence the largest of the four outputs will be in the case of $25^{12}$ and equals 52.
2) Answer (B)
We are given that the number ‘n’ can be written as “$abc$” in base 14 whereas we write the same number as “$acb$” in base 15.
n = $a*(14)^2 + b*(14) + c$
$\Rightarrow$ n = $196a+14b+c$ … (1)
Similarly, in base 15, we can write the number as “$acb$”.
n = $a*(15)^2 + c*(15) + b$
$\Rightarrow$ n = $225a+15c+b$ … (2)
In base 6, we can write the number as “$acac$”.
n = $a*(6)^3+c*(6)^2+a*(6)+c$
$\Rightarrow$ n = $222a+37c$ … (3)
By equation (2) and (3) we can say that,
$\Rightarrow$ $3a + b = 22c$ … (4)
As, $acac$ is a valid number in the number system of base 6, it would imply that both $a$ and $c$ are less than 6. We know that, 0 < a $\leq$ 5 and 0 $\leq$ b $\leq$ 13
Therefore, we can say that ‘c’ can be 1 only. At c = 2, R.H.S. becomes 44 which is not possible. Hence, we can say that ‘c’ = 1.
From equation (1) and (2) we get,
$196a+14b+c$ = $225a+15c+b$
$\Rightarrow$ $29a+14 = 13b$ … (5)
At c = 1, equation (4) will reduce to 3a + b = 22 … (6)
On solving equation (5) and (6) we get,
a = 4 and b = 10
We know that the numbers in base 14 = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D}
Hence, we can say that the number ‘n’ in base 14 = 4A1
Similarly, the numbers in base 145 = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E}
Hence, we can say that the number ‘n’ in base 15 = 41A
Therefore, the number ‘n’ in decimal system = $222*4+37*1 = 925$
Hence, the sum of the digits of the number ‘n’ in decimal system = 9 + 2 + 5 = 16.
3) Answer: 96
We can prime factorize the given number as follows:
$8690220=2^2*3^3*5*7*11^2*19$
We have to find the number of factors which are a multiple of 209 = 11*19. Therefore, we can say that we must have at least one 11 and 19 in each factor.
Hence, the number of factors of 8690220 which are also a multiple of 209 = (2+1)*(3+1)*(1+1)*(1+1)*(2)*(1) = 96
4) Answer (B)
It is given that the HCF of two numbers is 7. Let us assume that A = 7a and B= 7b where ‘a’ and ‘b’ are relatively co-prime numbers. Therefore, LCM of the two numbers = 7ab.
$\Rightarrow$ 7ab = 315
$\Rightarrow$ ab = 45
Hence, possible values of (a, b) = (1, 45), (5, 9), (9, 5) and (45, 1).
Therefore, (A, B) = (7, 315), (35, 63), (63, 35) and (315, 7). Thus, option B is the correct answer.
5) Answer (D)
x-y-z=20
x=20+y+z
Since x,y,z are positive integers,the minimum value value of x=22
Number of integral solutions = 1+2+3+4+5+6+7+7+6=41
D is the correct answer.
6) Answer: 31
From (x-10) to (x-98) there are $\frac{98-8}{2} = 45$ terms.
Since the number of terms are odd, any value of x from 1 to 9 will satisfy the inequality. Also, all value of x above 98 will not satisfy the inequality.
For x = 11,
there will be 1 positive term and 44 negative terms. Thus since the product will be positive, x=11 does not satisfy.
For x = 13,
there will be 2 positive term and 43 negative terms. Thus since the product will be negative, x=13 satisfies the inequality.
For x = 15,
there will be 3 positive term and 42 negative terms. Thus since the product will be positive, x=15 does not satisfy.
For x = 17,
there will be 4 positive term and 41 negative terms. Thus since the product will be negative, x=17 satisfies the inequality.
So on till x = 97 for which there will be 44 positive term and 1 negative term. Thus since the product will be negative, x=97 satisfies the inequality.
Thus we have to calculate the alternate odd numbers starting from 11.
Total number of odd numbers from 11 to 97 are $\frac{97-9}{2} = 44$.
Out of 44 only half of the odd numbers i.e. 22 numbers will satisfy the given inequality.
Thus total possible positive integral values of x = 22 + 9 = 31
Hence, 31 is the right answer.
7) Answer: 14
We are given that $ax^2 + bx – 4 = 0$
For real roots we can say that $b^2 – 4*a*(-4) \geq 0$
$\Rightarrow$ $b^2 \geq -16a$
We are given that both $a$ and $b$ $\in$ {-5, -3, -1, 0, 1, 5}
At $a = – 5$, $b^2 \geq 80$ Hence, there is no value of b for which the quadratic equation will have real roots.
At $a = – 3$, $b^2 \geq 48$ Hence, there is no value of b for which the quadratic equation will have real roots.
At $a = – 1$, $b^2 \geq 16$ Hence, b = 5, -5 are two possible solutions.
$a \neq 0$, Since ‘$a$’ is the coefficient of $x^2$.
At $a = 1$, $b^2 \geq -16$ Since $b^2$ is positive hence, $b$ can take all 6 values.
At $a = 5$, $b^2 \geq -80$ Since $b^2$ is positive hence, $b$ can take all 6 values.
Hence total number of distinct quadratic equations = 2 + 6 + 6 = 14.
8) Answer: 7
We are given that $\dfrac{1}{x^2 – 3x -18} + \dfrac{1}{x^2 – 3x -34} – \dfrac{2}{x^2 – 3x – 58} = 0$
Let us assume that $x^2 – 3x -18 = t$, then the equation can be written as,
$\Rightarrow$ $\dfrac{1}{t} + \dfrac{1}{t-16} = \dfrac{2}{t – 40}$
$\Rightarrow$ $\dfrac{t – 16 + t}{t*(t – 16)} = \dfrac{2}{t – 40}$
$\Rightarrow$ $\dfrac{2t – 16}{t*(t – 16)} = \dfrac{2}{t – 40}$
$\Rightarrow$ $(t – 8)(t – 40) = t(t – 16)$
$\Rightarrow$ $t^2 – 48t + 320 = t^2 – 16t$
$\Rightarrow$ $t = 10$, therefore, we can say that $x^2 – 3x -18 = 10$
$\Rightarrow$ $x^2 – 3x – 28 = 0$
$\Rightarrow$ $(x – 7)(x + 4) = 0$
$\Rightarrow$ $x = 7$ or $-4$. Hence, sum of all positive values of x = 7.
9) Answer (A)
We are given that $x^2+44x+656 = y^2$
$\Rightarrow$ $x^2+44x+656 = y^2$
$\Rightarrow$ $x^2+2*22x+484+172 = y^2$
$\Rightarrow$ $(x + 22)^2+172 = y^2$
$\Rightarrow$ $y^2- (x + 22)^2 = 172$
$\Rightarrow$ $(y – x – 22)(y + x + 22) = 172$
$\Rightarrow$ $(y – x – 22)(y + x + 22) = 2^2*43$
We can see that at least one of two $(y – x – 22)$ and $(y + x + 22)$ is even. We can easily see that if one of factor is even then other will also be an even number.
There is only one case when we have two even factors of 172 {2, 86} therefore we can say that
$y – x – 22 = 2$ and $y + x + 22 = 86$
Solving for $x,y$ $x$ = 20 and $y$ = 44
Therefore $x+y$ = 20 + 44 = 64
Hence option A is the correct answer.
10) Answer: 2
On simplification, $5x^2 – 4xy + 2y^2 – 3 = 2(x + 2y)$
$\Rightarrow$ $4x^2 – 4xy + y^2 +x^2 + y^2 – 3 = 2(x + 2y)$
$\Rightarrow$ $4x^2 – 4xy + y^2 +x^2 – 2x + 1 + y^2 – 4y + 4 = 3 + 1 + 4$
$\Rightarrow$ $(2x – y)^2 + (x – 1)^2 + (y – 2)^2 = 8$
We know that both x and y are integers hence we can say that all three parts $(2x – y)^2$, $(x – 1)^2$ and $(y – 2)^2$ has to be any number from {0, 1, 4}.
Sum of all three terms will be equals to 8 only when 2 out the 3 terms are 4-4 each and the remaining term has to be 0.
Case 1: $(2x – y)^2 = 0$ i.e. $y = 2x$
$\Rightarrow$ $ (x – 1)^2 + (2x – 2)^2 = 8$
$\Rightarrow$ $5x^2 – 10x – 3 = 0$ We get non integer values of $x$.
Case 2: $(x – 1)^2 = 0$ i.e. $x = 1$
$\Rightarrow$ $(2 – y)^2 + (y – 2)^2 = 8$
$\Rightarrow$ $ 2y^2 – 8y + 8= 8$ i.e. y = {0, 4}
Case 3: $(y – 2)^2 = 0$ i.e. $y = 2$
$\Rightarrow$ $(2x – 2)^2 + (x – 1)^2 = 8$
$\Rightarrow$ $5x^2 – 10x – 3 = 0$ We get non integer values of $x$.
We can see that points $(x, y)$ = (1, 0) and (1, 4) are two non-negative integral solutions.
International organizations for GK
11) Answer: 190
Let us try to simplify the expression.
$\dfrac{1}{x^2-18x-16} \leq \dfrac{5}{2}$
$\Rightarrow \dfrac{1}{x^2-18x+81-81-16} \leq \dfrac{5}{2}$
$\Rightarrow \dfrac{1}{(x^2-18x+81)-81-16} \leq \dfrac{5}{2}$
Let $(x-9) = t$. Putting it in the expression,
$\Rightarrow \dfrac{1}{t^2-97} \leq \dfrac{5}{2}$
Now, we know that the least value of $t^2$ possible is 0. At that value, LHS < RHS, thus the equation holds true.
RHS of the expression will always be negative for all values of $t \in [0,\sqrt{97})$
Here, $(x – 9)^2 < 97 $
$ \Rightarrow x < 9+\sqrt{97} $ and $ x > 9 – \sqrt{97} $
$ \Rightarrow x < 9+10 $ and $x < 9-10 $ (We have equated $\sqrt{97}$=10 because the smallest integral value of $t$ satisfying this condition will be 10)
$ \Rightarrow x < 19 $ and $x >-1$
Thus, the values of $x$ satisfying this condition are : 1,2….18.
Here, the value of $t$ cannot be $\sqrt{97}$ as then the denominator would become 0 and lead to an indeterminate form.
For all values of $t \geq \sqrt{97}$, the fraction is positive. In that case,
$ \dfrac{1}{t^2-97} \leq \dfrac{5}{2}$
$\Rightarrow t^2-97 \geq \dfrac{2}{5}$
$\Rightarrow t^2 \geq 97+\dfrac{2}{5}$
$\Rightarrow t^2 \geq 97.4$
$\Rightarrow t \geq 10$ (We have equated $\sqrt{97.4}$=10 because the smallest integral value of $t$ satisfying this condition will be 10)
Therefore $ t \in [0,\sqrt{97})U(\sqrt{97},\infty)$
Since $t = x-9$, therefore the range of $x$ can be computed by adding 9 to the range of $t$.
Thus, $ x \in [1,19)U(9+\sqrt{97},\infty)$
$\Rightarrow x \in [1,9+\sqrt{97})U(9+\sqrt{97},\infty)$
To count the integral values of $x$ which satisfy this equation, we put $\sqrt{97}$ = 10.
We do this because the equation becomes indeterminate only at one point, which is not equal to 10.
Thus at 10, the equation remains valid.
So, $x \in [1,9+10)U(9+10,\infty) $
We get a point of discontinuity at 19. Let us check if the equation is valid at 19 or not.
$\dfrac{1}{361-342-16} = \dfrac{1}{3} \leq {5}{2} $
Thus 19 is also included in the range of $x$.
So, $x \in [1,19]U[19,\infty) \Rightarrow x \in [1, \infty) $
Thus, the positive integral values of $x$ less than 20 which satisfy the equation are : 1,2,3…19
Sum of positive integral values = $\dfrac{19}{2} \times (1+19)$ = 190
12) Answer: 5
Ramesh mixes Rs. 20, Rs. 17 and Rs. 18 in the ratio a:b:c.
b is the geometric mean of a and c.
Let $a = 1, b = r$ and c = $r^2$
Let C be the CP of the rice obtained after mixing the 3 varieties.
Thus, 20a+17b+18c = C(a+b+c)
=> $20+17r+18r^2 = C(1+r+r^2)$
Thus, $20+17r+18r^2 = C+Cr+Cr^2$.
He marks up the price of the rice by 66.67%
Thus, the MP = 5C/3.
He gives a 20% discount on this and thus, the SP = $\dfrac{5C*0.8}{3}$ = $\dfrac{4C}{3}$
He makes a profit of Rs 6 while selling 1 kg rice.
=>$\dfrac{4C}{3} – C = 6$
=> $C/3 = 6$
Hence, C = 18.
Thus, $20+17r+18r^2 = 18+18r+18r^2$
=> $r = 2$
Hence, a:b:c = 1:2:4.
Thus, if he mixes Rs 17, Rs 18 and Rs 20 varieties of rice in the ratio 1:2:4, then the CP of the mixture will be $\dfrac{17*1+18*2+20*4}{1+2+4} = \dfrac{133}{7} = 19$.
Thus, the profit of Ramesh = 24-19 = Rs. 5.
Hence, 5 is the correct answer.
13) Answer: 40
The arrangement of the numbers is as follows.
Since Rinesh tries to arrange the numbers in sets of 5, It’s row and column numbers can be obtained by dividing the number by 5.
752 = 5*150+2
In 150 rows 750 numbers are arranged.
Now 751 occupies of odd numbered row column 1,752 occupies column 3
P=151,A=3
Similarly 1244 = 5*248 +4
In 248 rows 1240 numbers are arranged.
1241 occupies 249 row column 1,1242 occupies column 3,1243 occupies column 5,1244 occupies column 7
Q=249,B=7
P+Q=151+249=400
A+B=3+7=10
Required ratio = $\frac{400}{10}$
40 is the correct answer.
14) Answer: 500
Let the cost price of the article be $C$.
The shopkeeper sells the article at a profit of $x$%.
=> Price at which the person who bought the article bought the article = $(1+x)*C$
The person who bought the article sells it at a loss of $x$% to his friend.
Therefore, the friend who bought the article would have obtained it for $(1-x)(1+x)*C$ = $(1-x^2)*C$
Now, it has been given that the friend has obtained the article for $\frac{x}{4}$% less than the original price of the article.
=> $(1-x^2)*C$ = $(1-\frac{x}{4})*C$
$1-x^2 = 1-\frac{x}{4}$
$x^2 = \frac{x}{4}$
=> $x = \frac{1}{4}$
Now, we know that $C-(1-\frac{x}{4})*C = 100$
$C-(1-\frac{1}{16})*C=100$
$C*(\frac{1}{16}) = 100$
=> $C = 1600$
Price at which the friend bought the item = $1600 – 100$ = Rs.$1500$
Price at which the person bought the item = $(1+\frac{1}{4})*1600$ = Rs.$2000$.
=> Loss borne by the person = $2000-1500$ = Rs.$500$.
Alternate method:
We know that $\frac{x}{4}$% of the price of the article is Rs.100
=> $x$% of the price of the article = Rs.400.
We know that the person bought the article at $x$% greater than the price of the article and sold it at $\frac{x}{4}$% less than the price of the article.
=> Loss borne by the person = 400 + 100 = Rs.500.
15) Answer: 36950
The ratio of the amount is $\dfrac{1}{9} :\dfrac{1}{17} : \dfrac{1}{11} : \dfrac{1}{13}$
LCM of 9, 17, 11 and 13 is 21879
We can write the ratio as $\dfrac{21879}{9} :\dfrac{21879}{17} : \dfrac{21879}{11} : \dfrac{21879}{13}$
which is 2431 : 1287 : 1989 : 1683
Let the amounts distributed be 2431k, 1287k, 1989k, 1683k
It is given that 2431k – 1287k = 1144k = 5720
So, k = 5
Therefore, the total amount distributed = (2431 + 1287 + 1989 + 1683)*5 = Rs. 36950
Hence, 36950 is the correct answer.
16) Answer (C)
Let the profit earned from a trip by the company be ₹$x$, the number of passengers be $p$ and distance travelled be $d$.
Given, $ x \propto p^2$ and $x \propto d$
Combining the two proportionalities, $x \propto p^2d \Rightarrow x = kp^2d $ where k is the constant of proportionality.
We are given the ratio of profits earned per passenger. We need to find the trip which earned less overall ie we need to find the ratio of the total profit earned from the trips.
Let the average profit be $2a$ and $3a$ for the first and second trip respectively.
Thus, the ratio of overall profits of the two trips = $\dfrac{2a \times 30}{3a \times 15} = \dfrac{4}{3} $
Thus the second trip generated less overall profit. Therefore, the total profit in the second trip is ₹45000
Putting this in the expression for profit : $45000 = k \times (15)^2 \times 150 $
$ \Rightarrow k = \dfrac{45000}{225 \times 150} = \dfrac{4}{3} $
Now, profit for the first trip $p_{1} = k \times 15^2 \times 200 = 45000k$
Profit for the third trip $p_{2} = k \times 20^2 \times 300 = 120000k$
Thus, difference in profit = $p_{2} – p_{1} $
= $(120000-45000)k = 75000 \times \dfrac{4}{3} = ₹100000 $
17) Answer (A)

The conical tank is mounted as shown above.
Given, OA = 10 m, OD = 5 m
CD:AB = 2:1 (by similarity)
So, if area of base = $9R$
then area of cross section where CD is the radius = $\frac{9R}{4}$
Volume of tank = $\frac{1}{3}\times 9R \times 10$ = 30$R$
Volume of tank below upto CD= $\frac{1}{3}\times \frac{9R}{4} \times 5=\frac{15R}{4}$
Since, the inlet fills the entire tank in 10 hrs
Rate of inlet = $\frac{30R}{10}=3R$ litre/hr
Rate of outlet = $\frac{1}{2} \times \frac{30R}{10}=\frac{3R}{2}$ litre/hr
Time taken to fill the tank till the level of outlet pipe = $\frac{\frac{15R}{4}}{3R}$= 1.25 hrs
Remaining volume to be filled = $30R-\frac{15R}{4}=\frac{105R}{4}$
Time taken to fill = $\frac{\frac{105R}{4}}{\frac{3R}{2}}$ = 17.5 hrs
$\therefore$ Total time taken = 17.5 + 1.25 = 18.75 hrs
Hence, option A is the correct answer.
18) Answer (A)
Let the speed of Golu be $g$, speed of escalator be $e$ and the distance travelled be $d$.
Time taken to climb up an escalator coming down $t_1 = \dfrac{d}{g-e} $
Time taken to climb up an escalator going up $t_2 = \dfrac{d}{g+e} $
Given, $\dfrac{t_1}{t_2} = \dfrac{9}{4} $
$ \Rightarrow \dfrac{\frac{d}{g-e}}{\frac{d}{g+e}} = \dfrac{9}{4} $
$ \Rightarrow \dfrac{g+e}{g-e} = \dfrac{9}{4} $
$ \Rightarrow 4g + 4e = 9g – 9e $
$ \Rightarrow 5g = 13e $
$ \Rightarrow g = 2.6e $
Also, $\dfrac{d}{g+e} + \dfrac{d}{g-e} = 208 $
As $g=2.6e$, $g+e = 3.6e$ and $g-e=1.6e$
Hence, $\dfrac{d}{g+e}=\dfrac{4}{9} \times \dfrac{d}{g-e}$
Therefore,$(\dfrac{4}{9} \times \dfrac{d}{g-e}) + \dfrac{d}{g-e} = 208 $
$ \Rightarrow \dfrac{d}{g-e} \times (\dfrac{4}{9} + 1) = 208 $
$ \Rightarrow \dfrac{d}{g-e} \times \dfrac{13}{9} = 208 $
$ \Rightarrow \dfrac{d}{1.6e} = 208 \times \dfrac{9}{13} $
$ \Rightarrow \dfrac{d}{1.6e} = 144 $
$ \Rightarrow d = 144 \times 1.6e = 230.4e $
Now, time required $t_3 = \dfrac{d}{g – \frac{e}{2}} $
$ \Rightarrow t_3 = \dfrac{230.4e}{2.6e – 0.5e} $
$ \Rightarrow t_3 = \dfrac{230.4}{2.1} \approx 110$ seconds
19) Answer (C)
Let the speed of cruise X and cruise Y be $x$ and $y$ km/hr respectively.
At 6:00 AM when the cruises meet, the distance travelled by X, $d_x = 9x $ kms
The distance travelled by Y, $d_y = y $ kms
Given, $\dfrac{d_x}{d_y} = 4 \Rightarrow \dfrac{9x}{y} = 4 \Rightarrow \dfrac{x}{y} = \dfrac{4}{9} $
Also, distance travelled by Y, $d_y = \dfrac{1}{5} \times 1000 = 200$ kms
Speed of Y, y = 200 km/hr
Speed of X, $ x = \dfrac{4y}{9} = \dfrac{800}{9} $ km/hr
Now, we need to give a headstart to X (since $\frac{800}{9} < 200$).
Time taken by X to cover 1000 kms = $\dfrac{1000}{x} = \dfrac{1000 \times 9}{800}$ = 11.25 hrs
Time taken by Y to cover 1000 kms = $\dfrac{1000}{200} $ = 5 hrs
Thus, the headstart given to X will be of (11.25 – 5) = 6.25 hours
Thus, headstart given to X = $\dfrac{25}{4} \times \dfrac{800}{9} = \dfrac{5000}{9} $ = 555.55 kms
20) Answer (B)
Let the capacity of the tank be $100a$ units
Till the point when the water level is over the level of the first pipe, both the pipes will remove water from the tank. After the water level goes down, only the pipe in the bottom will be used.
Let the capacity of the pipes be $x$ units.
Now, to empty a full tank of water, the time needed $t_{1} = \dfrac{70a}{x+x} + \dfrac{30a}{x} $
$\Rightarrow t_{1} = \dfrac{35a}{x} + \dfrac{30a}{x} $
$\Rightarrow t_{1} = \dfrac{65a}{x} $ — (1)
To empty a 80% full tank of water, the time needed $t_{2} = \dfrac{50a}{2x} + \dfrac{30a}{x} $
$\Rightarrow t_{2} = \dfrac{55a}{x} $ — (2)
Given, $t_{1} – t_{2} = 10 $
$ \Rightarrow \dfrac{65a}{x} – \dfrac{55a}{x} = 10$ hours
$ \Rightarrow \dfrac{65a}{x} – \dfrac{55a}{x} = 10$
$ \Rightarrow \dfrac{10a}{x} = 10$
$ \Rightarrow \dfrac{a}{x} = 1$
$ \Rightarrow a = x$
Capacity of inlet pipes = $2x$
Total capacity of inlet pipes = $4 \times 2x = 8x$
Time taken to fill the tank = Time taken to fill 30% tank + Time taken to fill the rest 70%
$t = \dfrac{30x}{8x-x} + \dfrac{70x}{8x-2x} $
$\Rightarrow t = \dfrac{30}{7} + \dfrac{70}{6} $
$\Rightarrow t = \dfrac{(30 \times 6)+(70 \times 7)}{42} $
$\Rightarrow t = \dfrac{(180)+(490)}{42} $
$\Rightarrow t = \dfrac{(180)+(490)}{42} $
$\Rightarrow t = \dfrac{670}{42} = \dfrac{335}{21} = 16 $ hours
Functions & Inequalities Questions For XAT Preparation
21) Answer (A)
A and B will start working together on building X while C starts working on building Y.
Let the total work on foundation be $8p$ units.
Work completed daily by A = $\dfrac{8p}{8} = p$ units/day = work completed daily by B
Therefore, work completed daily by A and B together = $p+p = 2p$ units/day
Therefor, A and B will work together on building X’s work for $\dfrac{8p}{2p} = 4$ days.
Let the total work on walls of Building Y be $120q$ units.
Work completed daily by A = $\dfrac{120q}{10} = 12q$ units/day
Work completed daily by B = $\dfrac{120q}{8} = 15q$ units/day
Work completed daily by C = $\dfrac{120q}{6} = 20q$ units/day
Therefore, work completed by C in 4 days = $(20q) \times 4 = 80q$ units
So, work left in building Y when A,B,C start working together = $120q – 80q = 40q$
Work done daily when A,B,C start working together = $12q+15q+20q = 47q$
Therefore, A,B,C will work together for 1 day on work on building Y.
Total money earnt by B = Money earnt for work on building X + money earnt for work on building Y + daily wages
= $(\dfrac{1}{2} \times 10000) + (\dfrac{15}{47} \times {40q}) + (5 \times 500)$
= $(5000) + (\dfrac{15}{47} \times 40 \times \dfrac{18000}{120}) + (2500)$ [$\because$ 120q=18000]
= $(5000) + (1915) + (2500) = ₹9,415/-$
22) Answer: 4
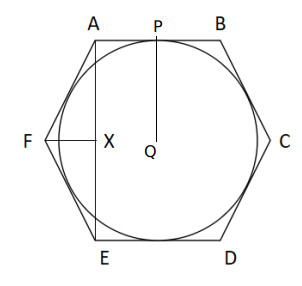
We need to first calculate the circumference of the circle along which Baldev runs.
We know that the interior angle of a Hexagon is 120 degrees.
Also, EAB will be 90 degrees.
Thus, angle FAX will be 30 degrees.
In right-angled triangle FAX, we get,
Cos 30 = AX/AF
Thus, $\dfrac{\sqrt{3}}{2} = \dfrac{AX}{\frac{7}{\sqrt{3}}}$
Thus, $AX = \dfrac{7}{2}$
PQ=AX
We know that PQ = radius of the circle.
Thus, circumference of the circle along which Baldev runs = $2\pi r$ = $2*\dfrac{22}{7}*\dfrac{7}{2}$
= 22 m.
The circumference of the track along which Amit runs = $6*\dfrac{7}{\sqrt{3}}$ = $14\sqrt{3}$
Time required by Baldev to finish the race = $\dfrac{22}{2} = 11$ seconds.
Time required by Amit to finish the race = $\dfrac{14\sqrt{3}}{2\sqrt{3}} = 7$ seconds.
Thus, If they both finish the race at the same time, Amit must have given Baldev a head start of 4 seconds.
Hence, 4 is the correct answer.
23) Answer (A)
Let us denote Aman, Bhushan and Chintu by A, B, and C.
They will take the minimum time to reach the station when C walks and A andB leave on a bike and either A or B comes back to pick up C(let us assume that A comes back)
A,B will reach the station in $\dfrac{36}{48}$ = 0.75 hour.
In this 0.75 hour, C would have covered 0.75*8 = 6 km.
The distance between C and A now is 30 km.
The relative speed of C w.r.t A = 8+48 = 56 km/hr.
Thus, A and C will meet after $\dfrac{30}{56} = \dfrac{15}{28}$ hour.
The distance covered by C in this $\dfrac{15}{28}$ hour = $\dfrac{8*15}{28} = \dfrac{30}{7}$
The distance remaining between C and station is now $30-\dfrac{30}{7}$ = $\dfrac{180}{7}$ km.
They’ll cover this distance is $\dfrac{180}{7*48}$ = $\dfrac{15}{28}$ hour.
Thus, the total time required for all the 3 friends to reach the station is $0.75+\dfrac{15}{28}+\dfrac{15}{28} \approx 1.82$ hours.
Hence, option A is the correct answer.
24) Answer (B)
Let the speed of Natwarlal be $x$ m/s = $x$ steps/s
While going up the ascending escalator of moving at $2$ steps/s he covers $100$ steps in $20$ s
Thus, $x+2 = \frac{100}{20} = 5$
Hence, $x = 3$ m/s or $3$ steps/s
Niharilal catches Natwarlal after a total of $80$ seconds.
Thus, Natwarlal traveled for $60$s after reaching the top of the escalator.
Thus, distance traveled after reaching the top of the escalator = $60*3 = 180$m
Let the speed of Niharilal be $v$ m/s or $v$ steps/s
In $80$ seconds, he travels by escalator and then on the plain road.
He travels $100$m on then $180$m on the plain road.
Thus, $80 = \frac{100}{v-2} + \frac{180}{v}$
=> $4v(v-2) = 5v+9(v-2)$
Solving we get $v = 1 m/s$ or $v = 4.5 m/s$
But if $v = 1 m/s$ then Niharilal will not be able to catch Natwarlal.
Hence, speed of Niharilal = $4.5 m/s$
Hence, the required ratio = $3:4.5 = 2:3$
Hence, option B is the correct answer.
25) Answer (D)
Given, fruit vendor buys at the cost price to the whole-seller.
Let, us assume the cost price of an apple = Re 1
For the first 200 apples:
The vendor must have paid for only 160 and obtained the remaining 40 by deceit.
So, for the whole seller:
CP= Rs 200
SP= Rs 160
For the remaining 400 apples:
The vendor would have paid Rs 5 per 3 apples.
So, for the whole-seller:
CP= Rs 400
SP= Rs $400\times \frac{5}{3}$ = Rs $\frac{2000}{3}$
Total CP= Rs (400 + 200) = Rs 600
Total SP = Rs (160 + $\frac{2000}{3}$) = Rs $\frac{2480}{3}$
$\therefore$ Profit % = $\frac{\frac{2480}{3}-600}{600}\times 100$% $\approx$ 37.78%
26) Answer (D)
Let us assume that the cost price of the mobile = $7x$
Then the marked price of the mobile = $1.1428*7x = 8x$
Let the percent of discount he offered on the mobile, and the profit/loss he incurred be in the ratio of 4y : 5y.
Therefore we can say that
$\Rightarrow$ $8x(1-\dfrac{4y}{100}) = 7x(1\pm\dfrac{5y}{100})$
$\Rightarrow$ $\dfrac{8x}{7x}$ = $\dfrac{(1\pm \dfrac{5y}{100})}{(1-\dfrac{4y}{100})}$
$\Rightarrow$ $\dfrac{8}{7}$ = $\dfrac{100\pm 5y}{100-4y}$
We can see that in L.H.S. numerator is greater than denominator hence,
$\Rightarrow$ $\dfrac{8}{7} = \dfrac{100+5y}{100-4y}$
$\Rightarrow$ $800-32y = 700+35y$
$\Rightarrow$ $y = \dfrac{100}{67}$
Therefore, the profit percentage made by the seller = $5y = \dfrac{500}{67}$ = 7.46% profit.
27) Answer: 0
$a^b = 125$
Taking log to the base 5 on both the sides, we get,
$b*log_{5}{a} = log_{5}{125} = 3$
Let $log_{5}{a} = r$
So, $b * r = 3$ …(1)
We have, $b = [log_{5}{a}]^3 + 12*[log_{5}{a}] – 6 * [log_{5}{a}]^2 – 8 $ …(2)
Using equation (1) and (2),
$ \frac{3}{r} = r^3 + 12r – 6r^2 – 8$
$3 = r * (r-2)^3$
Since r is an positive integer,
$r = 3$
Thus, $b = 1$ and $a = 125$
Hence, $log_{5}{b}$ = $log_{5}{1}$ = 0
28) Answer (D)
The expansion of $(\sqrt[8]{x} + \sqrt[6]{y})^{72}$ will be $\sum_{a=0}^{72} (^{72}C_{a} x^{\frac{a}{8}} y^{\frac{72-a}{6}})$
Now for integral powers of x and y, (a) must be a multiple of 8 and (72-a) multiple of 6 or ‘a’ must be a multiple of both 6 and 8.
Between 0 and 72, only such numbers are 0, 24, 48, and 72.
So, the sum of such expressions will be
$y^{12} + ^{72}C_{24} x^3 y^8 + ^{72}C_{48} x^6 y^4 + x^9$ = $ y^{12} + 3\left( x^3 y^8 + x^6y^4 \right) + x^9 + k\left(x^3 y^8 + x^6y^4\right) $
= $(x^3 + y^4)^3 + k\left(x^3 y^8 + x^6y^4\right)$
We can see that A can divide the term with ‘k’ as common but not the term which is cubed.
Similarly, B can divide the term which is cubed but not necessarily the term which has ‘k’ in common.
C can divide all the terms which have $(x^3y^8 + x^6y^4)$
i.e. it can completely divide $^{72}C_{48} \left(x^3y^8 + x^6y^4 \right )$ , but cannot necessarily divide $x^9 + y^{12}$.
So, none of the options necessarily divides the expression.
Thus, D is the correct answer.
29) Answer: 141
The number of digits in $a^{n}$ base k is given by $nlog_{k}a + 1$
In this case n =35, k =7, a = 2401
So the number of digits in $(2401^{35})_7 $ = $35log_{7}2401 + 1$
=> 35*4 + 1 = 141
30) Answer: 2
$log_{b}a+ log_{ab}a^2 + log_{a^{2}b}a^{3} =0$
=> $\frac{1}{log_{a}b}+ \frac{1}{log_{a^2}ab} + \frac{1}{log_{ a^{3}} a^{2}b } =0$
=>$\frac{1}{log_{a}b}+ \frac{2}{log_{a}a+ log_{a}b } + \frac{3}{2log_{a}a+ log_{a}b } =0$
Assume $log_{a}b$ as x.
=> $\frac{1}{x}+ \frac{2}{1+x} + \frac{3}{2+x} =0$, solving which we get
=> $x^2+3x+2+3x+3x^2+4x+2x^2=0$ or $6x^2+10x+2=0$ or $3x^2+5x+1=0$
Solutions for this equation will be $x=\frac{-5\pm \sqrt{25-12}}{6}$
We can see that both the solutions are real since the discriminant of the above equation is positive. Let’s say the two solutions are x1 and x2.
=> There 2 solution possible for b-> one $b=a^{x1}$ and other $b=a^{x2}$.
Logarithm Questions For XAT Preparation
31) Answer: 342
With even perimeter and integral sides, we can form a triangle whose all the sides are even or else whose two sides are odd and the third side is even.
Perimeter = 150
Let the sides of the triangle be a, b, c
a+b+c=150
Number of triangles with two odd, one even side = Total number of possible triangles – number of triangles whose all the sides are even.
Now, the number of triangles with integral sides having perimeter p is given by
1. <$\frac{p^2}{48}$> if p is even where < > denotes the nearest integer.
2. <$\frac{(p+3)^2}{48}$> if p is odd
Number of triangle possible when the perimeter is 150 = <$\frac{p^2}{48}$> = <$\frac{150^2}{48}$> = <468.75> = 469
When all the sides are even, 2k+2m+2n=150
=> k+m+n=75
Number of triangles possible with integral sides = <$\frac{(p+3)^2}{48}$> = <$\frac{78^2}{48}$> = <126.75> = 127
Number of triangles with two odd, one even side = 469 – 127 =342
Alternate Approach:
Let’s find the number of possible triangles
The largest side can be 74 ($\because$ Sum of two sides should be greater than the third side)
74-x+74-y+74-z=150 where x, y, z can be $\geq$ 0
222-(x+y+z)=150
x+y+z=72
Number of possible values of x, y, z=$^{72+3-1}C_{3-1}$
=$^{74}C_2$
=2701
Number of Isosceles triangles 2x+y=72
x can vary from 0 to 36, out of which there will be a possibility of an equilateral triangle
Number of isosceles triangles=36, equilateral triangle = 1
Number of scalene triangles = $\frac{2701-3*36-1}{3!}$
=432
Number of possible triangles = 432+36+1=469
Number of triangles with all the three sides even.
a+b+c=150
74-2x+74-2y+74-2z=150
2x+2y+2z=222-150=72
x+y+z=36
Number of integral solutions = $^{36+3-1}C_{3-1}$
=703
Number of isosceles triangles =2x+y=36
x can vary from 0 to 18 so 19 possibilities out of which 1 is a possibility of an equilateral triangle.
Number of scalene triangles = $\frac{703-3*18-1}{3!}$
=108
Number of possible triangles with all the three even sides=108+18+1=127
So the number of triangles with two odd and one even side=469-127
=342
342 is the correct answer.
32) Answer: 13
Out of 8 subjects,the two subjects which are placed in the correct rack can be selected in $^8C_2$ ways
=28 ways
The remaining 6 books are not placed in the correct rack.The number of ways this can happen is given by derangement which is given by
6![1-$\frac{1}{1!}$ +$\frac{1}{2!}$ – $\frac{1}{3!}$ + $\frac{1}{4!} $-$\frac{1}{5!}$+$\frac{1}{6!}$]
=265
No of arrangements possible = 28*265
=7420
sum of digits of 7420 is 13
Hence 13 is the correct answer.
33) Answer: 31
We know that if a number is expresses as
$n = a^p * b^q * c^r$
Then, the number of factors = $(p + 1)(q + 1)(r + 1)$
Here, the number has 61 factors where 61 is a prime number.
So, 61 cannot be obtained as a product of two different numbers except taking 1 as the second number.
Therefore, the square of the given number can be expressed.
$n^2 = x^{60}$
So, the number can be expressed as
$n = x^{30}$
The number of factors of $n$ = 31
Hence, 31 is the correct answer.
34) Answer: 4
N is a 7 digit number
Leftmost digit can be 1,2,3 or 4
1: Leftmost digit of N is 1
Sum of the remaining 6 digits = 3 .Other digits can be 1,1,1 and 3 zeros or 2,1,0,0,0,0 or 3,0,0,0,0,0
No of possibilities when other 6 digits are in the form (111000) = $\frac{6!}{3!*3!}$ = 20
No of possibilities when other 6 digits are in the form (210000) = $\frac{6!}{4!}$ = 30
No of possibilities when other 6 digits are in the form (300000) = $\frac{6!}{5!}$ = 6
2: Leftmost digit of N is 2
Sum of the remaining 6 digits = 2 .Other digits can be 1,1 and 4 zeros or 2,0,0,0,0,0
No of possibilities when other 6 digits are in the form (110000) = $\frac{6!}{4!*2!}$ = 15
No of possibilities when other 6 digits are in the form (200000) = $\frac{6!}{5!}$ = 6
3: Leftmost digit of N is 3
Sum of the remaining 6 digits = 1 .Other digits can be 1,0,0,0,0,0,0
No of possibilities when other 6 digits are in the form (100000) = $\frac{6!}{5!}$ = 6
There is 1 possibility when the leftmost digit is 4
Total number of possibilities of N
M = 20+30+6+15+6+6+1
=84
Sum of factorial of each digit in M =8!+4!
Remainder when sum of factorial of each digit in M when divided by 10 = 4*3*2 mod 10 = 4(because 8! mod 10 is 0)
Hence 4 is the correct answer.
35) Answer (C)
$ x^2 – 6x = 8y – y^2$
=> $x^2 – 6x + y^2 – 8y = 0$
=> $x^2 – 6x + 9 + y^2 – 8y + 16 = 25$
=> $(x-3)^2 + (y-4)^2 = 5^2$
Thus, the equation represents a circle with center (3, 4) and radius 5 units.
Let us find the distance between the line and the point (3,4).
If the distance is more than 5 units, then the line and the circle do not intersect.
If the distance is exactly 5 units, then the line and the circle intersect at exactly 1 point and if the distance is less than 5 unit then the line and the circle will intersect twice.
The first line is => $ y = \sqrt{3}x – (6+3\sqrt{3})$
In this line, slope $m = \sqrt{3}$, and $c = -(6+3\sqrt{3})$
Thus, the distance between the line and the center (3,4) is $\dfrac{|4 – 3\sqrt{3} + 6+3\sqrt{3}|}{\sqrt{1+(\sqrt{3})^2}}$ = $\dfrac{10}{2} = 5$
Thus, the distance is exactly 5 units and hence, there is only 1 point of intersection.
The second line is $ y -1 = x – 6\sqrt{2}$
In this line, slope $ m = 1,$ and $ c = -(6\sqrt{2} – 1)$
Thus, the distance between the line and the center of circle (3,4) is $\dfrac{|4 – 3*1 + 6\sqrt{2}-1|}{\sqrt{1+{1^2}}} = 6$
Thus, the distance between the line and the center of circle is 6 units.
6 units > 5 units and thus, there is no point of intersection.
Since, the slope of both the lines is different. they’ll intersect at 1 point( roughly at [-6.2, 1.4])
Thus, there are 2 points of intersection.
Hence, option D is the correct answer.
36) Answer: 96
We have $f(x,k).f(x,k+1) = 1$
Put k = 1
$f(x,1).f(x,2) = 1$
$f(x,1) = \frac{1}{f(x,2)}$
For k = 2
$ f(x,2) = \frac{1}{ f(x,3)}$
So, $f(x,1) = \frac{1}{f(x,2)} = f(x,3) = \frac{1}{ f(x,4)} $ and so on
Thus $f(x,odd).f(x,even) = 1$
If k is odd then k.(k+4) is odd and (k+3)(k+5) is even
If k is even then k.(k+4) is even and (k+3)(k+5) is odd
So |$ \sum_{k=5}^{100}(f(x,k.(k+4))*f(x,(k+3).(k+5)))$|
= $ \sum_{k=5}^{100}(1)$
= 96
37) Answer (C)

From the figure we see that Q is centroid and AQD =30.
In triangle AQS, QAS and AQS are both 30. Hence, ASD = 30+30 =60……(1)
Also, angle PDS=30…(2)
From (1) and (2), DPS=90
From symmetry, AP=DP=EU=BU
In right triangle, APT assume AP = x, AP=ATcos60 => AT=2x, Similarly, PT = $\sqrt{3}$ x
Using symmetry PT=UT
AB = a = AT+UT+BT = 2x + $\sqrt{3}$x +x
=> x= $\frac{a}{3+\sqrt{3}}$
Now the area not overlapped = 6*(1/2)*AP*PT = $3\sqrt{3}$x$^2$ = $3\sqrt{3} (\frac{a}{3+\sqrt{3}})^2$ = ${\frac{\sqrt{3}a^2}{4+2\sqrt{3}}}$
38) Answer (A)
Let us name all the points in the figure. This will help us in calculating the areas and the costs associated with each area.

From the figure, we know that the blue coloured regions are indigo plantations and the yellow coloured region is the wheat plantation.
Let the length of the piece of land be $l$ and breadth be $b$.
Thus, the area of land = $l \times b = lb$ sq units
Area of one small rectangle = $\dfrac{1}{9} \times lb $
Let the ratio of sides of rectangle and the piece of land be $r$
Thus, length of rectangle = $r \times$ length of piece of land
Also, breadth of rectangle = $r \times$ breadth of piece of land
Area of small rectangle = $(r \times l) \times (r \times b) = r^2 \times lb$ sq units
Now, we know that, $\dfrac{r^2 \times lb}{lb} = \dfrac{1}{9} $
$ \Rightarrow r^2 = \dfrac{1}{9} \Rightarrow r = \dfrac{1}{3} $
Thus, length of rectangle = $\dfrac{AB}{3} = \dfrac{l}{3} $
Also, breadth of rectangle = $\dfrac{AD}{3} = \dfrac{b}{3} $
Now, AN+NE+EB = AB
$\dfrac{l}{3}+NE+\dfrac{l}{3} = l \Rightarrow NE = \dfrac{l}{3} $
Now, AL+LJ+JD = AD
$\dfrac{b}{3}+LJ+\dfrac{b}{3} = b \Rightarrow LJ = \dfrac{b}{3} $
Now, area of the wheat plantation = Area of MNEF + Area of MFKI + Area of MIJL
=> area of wheat plantation = $(\dfrac{l}{3} \times \dfrac{b}{3}) + (\dfrac{l}{3} \times \dfrac{b}{3}) + (\dfrac{l}{3} \times \dfrac{b}{3}) $
=> area of wheat plantation = $ \dfrac{lb}{9} + \dfrac{lb}{9} + \dfrac{lb}{9} $
=> area of wheat plantation = $ \dfrac{lb}{3} $ sq units
Cost of ploughing the wheat plantation = $ \dfrac{lb}{3} \times 15 = ₹5lb $
Area of indigo plantation = 2 x Area of rectangle = $ 2 \times (\dfrac{lb}{9}) = \dfrac{2lb}{9} $
Cost of ploughing the indigo plantation = $ \dfrac{2lb}{9} \times 20 = ₹\dfrac{40lb}{9} $
Ratio = $\dfrac{5lb}{\frac{40lb}{9}} = \dfrac{45}{40} = \dfrac{9}{8} $
39) Answer (C)
Let us name a few more points on the figure to help us with the solution.

Let us first try to find the area of rectangle MNOP ie $A_{1}$.
Since I,J,K,L are mid-points of the line segments, we know that they are parallel. Thus, OP = MN = EF = GH.
Now, since G and H are midpoints of side of square, we can apply pythagoras theorem to $\triangle$HGD
Thus, $DG^2 + DH^2 = HG^2$
$\Rightarrow (\dfrac{10}{2})^2 + (\dfrac{10}{2})^2 = HG^2 $
$ \Rightarrow 25 + 25 = HG^2 $
$ \Rightarrow HG = \sqrt{50} = 5 \sqrt{2} $ units.
We also know that ON = MP.
To find ON, we join JK. Then, we apply pythagoras theorem in $\triangle$CJK
So, $JK^2 = CJ^2 + CK^2 $
$ \Rightarrow JK^2 = (\dfrac{10}{2 \times 2})^2 + (\dfrac{10}{2 \times 2})^2 $
$ \Rightarrow JK^2 = 2 \times \dfrac{25}{4} $
$ \Rightarrow JK^2 = \dfrac{50}{4} $
$ \Rightarrow JK = \sqrt{\dfrac{50}{4}} = \dfrac{5 \sqrt{2}}{2} $
From figure, we know that JK = ON.
Thus, area of rectangle MNOP $A_{1} = MN \times ON $
$ \Rightarrow A_{1} = (5 \sqrt{2}) \times (\dfrac{5 \sqrt{2}}{2}) $
$ \Rightarrow A_{1} = 25 $ square units.
Observe $\triangle$GOK and $\triangle$FNJ
$\angle$OGK = $\angle$NFJ and $\angle$OKG = $\angle$NJF (angles opposite equal sides)
Thus by AAA property, $\triangle GOK \sim \triangle JNF $
Since GK = JF, therefore $\triangle GOK \cong \triangle JNF $
Thus, $OG = FN = \dfrac{FG}{2} = \dfrac{5 \sqrt{2}}{2} $
So, area of rectangle EFNM = area of rectangle OGHP $A_{2} = FN \times EF $
$ \Rightarrow A_{2} = (\dfrac{5 \sqrt{2}}{2 \times 2}) \times (5 \sqrt{2}) $
$ \Rightarrow A_{2} = \dfrac{25}{2} $ square units.
Area of shaded region in $\triangle$LDK $A_{3}$ = Area of $\triangle$LDK – $A_{2}$
$ \Rightarrow A_{3} = [\dfrac{1}{2} \times (5 + \dfrac{5}{2}) \times (5 + \dfrac{5}{2}) ] – \dfrac{25}{2}$
$ \Rightarrow A_{3} = \dfrac{225}{8} – dfrac{25}{2} $
$ \Rightarrow A_{3} = \dfrac{125}{8} $ square units.
Since the figure is symmetrical, area of shaded region in $\triangle$EFB is also equal to $A_{3}$
Thus, total shaded area $A = [ 2 \times A_{3} ] + A_{1} $
$ \Rightarrow A = [2 \times \dfrac{125}{8} ] + 25 $
$ \Rightarrow A = \dfrac{225}{4} $ square units.
Thus, m+n = 225+4 = 229
40) Answer (C)
The slope of the given line 2x-4y=5 is 0.5 and thus, the slope of the line containing (1,2) and it’s reflection is -2.
Thus, the equation of this line will be:-
y-2 = -2(x-1)
=> y-2 = -2x + 2
I.e 2x+y = 4.
The point of intersection of 2x-4y=5 and 2x+y = 4 will be the mid-point of (1,2) and A.
The point of intersection of these 2 lines can be found out by subtracting 1 equation from the other.
The point of intersection comes out to be (2.1, -0.2)
This point is the mid-point of the line joining (1,2) and A(p,q)(assume).
Thus, we get $\dfrac{p+1}{2} = 2.1 => p = 3.2$ and $\dfrac{q+2}{2} = -0.2 => q = -2.4$
Thus, A = (3.2, -2.4)
The slope of the given line x-y=3 is 1 and thus, the slope of the line containing (1,2) and it’s reflection is -1.
Thus, the equation of this line will be:-
y-2 = -1(x-1)
=> y-2 = -x + 1
I.e x+y = 3.
The point of intersection of x-y=3 and x+y=3 will be the mid-point of (1,2) and B.
The point of intersection of these 2 lines can be found out by adding 1 equation to the other.
The point of intersection comes out to be (3, 0).
This point is the mid-point of the line joining (1,2) and B(l,m)(assume).
Thus, we get $\dfrac{l+1}{2} = 3 => l = 5$ and $\dfrac{m+2}{2} = 0 => m = -2$
Thus, B = (5,-2)
Thus, the distance between A and B = $\sqrt{(5-3.2)^2 + (-2+2.4)^2} = \sqrt{1.8^2 + 0.4^2} = \sqrt{3.4}$
Hence, option C is the correct answer.
Mensuration Questions for XAT Preparation
41) Answer (A)
Let us draw the diagram first,
Let us assume that length of SQ and PR be ‘$a$’ and ‘$b$’ units respectively.
Therefore the area of $\triangle$OUR = $\dfrac{\text{Area of triangle OQR}}{2}$ = $\dfrac{1}{2}*\dfrac{1}{2}*\dfrac{a}{2}*\dfrac{b}{2}$ = $\dfrac{ab}{16}$
the area of $\triangle$SQR = $\dfrac{1}{2} * SQ * OR$ = $\dfrac{1}{2} * a * \dfrac{b}{2} = \dfrac{a*b}{4}$
From the symmetry we can see that Area of $\triangle$VUR = $\dfrac{1}{2}$*$\triangle$ORQ = $\dfrac{1}{4}$*$\triangle$SQR
Hence the area of $\triangle$VUR = $\dfrac{a*b}{16}$
Area of rhombus OURV = 2*area of $\triangle$OUR = $\dfrac{a*b}{8}$
Area of $\triangle$OVU = $\dfrac{a*b}{8} – \dfrac{a*b}{16}$ = $\dfrac{a*b}{16}$
Since M and N are the mid points of OV and OU hence, Area of $\triangle$OMN = $\dfrac{1}{4}$*$\triangle$OVU = $\dfrac{a*b}{64}$
Hence, the area of the pentagon MNURV = Area of rhombus OURV – Area of triangle OMN = $\dfrac{a*b}{8}$-$\dfrac{a*b}{64}$ = $\dfrac{7ab}{64}$.
We can see that quadrilateral WTNM are trapezium.
Height of the trapezium WTNM = $\dfrac{b}{4}$ + $\dfrac{b}{8}$ = $\dfrac{3b}{8}$
Therefore, the area of trapezium WTNM = $\dfrac{1}{2}*(WT + MN)*\dfrac{3b}{8}$ = $\dfrac{1}{2}*(\dfrac{a}{2} + \dfrac{a}{4})*\dfrac{3b}{8}$ = $\dfrac{9ab}{64}$
Hence, the ratio of the area of pentagon MNURV to area of quadrilateral WTNM = $\dfrac{7ab}{64}$ : $\dfrac{9ab}{64}$ = $7 : 9$
Thus, option A is the correct answer.
42) Answer (C)
Let ‘$r$’ be the radius of the circle then the longer side of the rectangle = $5*2r = 10r$

We see that joining the centers of the given circles we get a hexagon of length 2r. The breadth is AE + 2r. We can find AE by using the fact that the internal angle of a hexagon is 120º.
1/2 * AE = AF sin 60 = 2r * √3/2 = r√3. => AE = $2(\sqrt{3}r)$
Length of the shorter side = $2r + AE$ = $2r + 2(\sqrt{3}r)$ = $2r(\sqrt{3} + 1)$
Hence, the ratio of the longer side of the rectangle to the shorter side = $\dfrac{10r}{2r(\sqrt{3} + 1)}$
$\Rightarrow$ $\dfrac{5}{(\sqrt{3} + 1)}$
Multiplying and dividing by $(\sqrt{3} – 1)$
$\Rightarrow$ $\dfrac{5(\sqrt{3} – 1)}{(\sqrt{3} + 1)(\sqrt{3} – 1)}$
$\Rightarrow$ $\dfrac{5\sqrt{3} – 5}{2}$
$\Rightarrow$ $\dfrac{\sqrt{75} – 5}{2}$
Hence we can say that A = 75 and B = 5
Therefore, the value of $\dfrac{A}{B}$ = $\dfrac{75}{5}$ = $15$
Thus, option C is the correct answer.
43) Answer: 135
Let S be the midpoint of QR. Then by SAS Congruence, $\triangle$PQS $\cong$ $\triangle$PRS so $\angle$PSQ = $\angle$PSR = 90°.
Now let QS = y and PQ = x and $\angle TQS$ = $\dfrac{\angle PQS}{2} = \theta$.
Then $cos\theta$ = $\dfrac{y}{10}$ … (1)
and $cos(2\theta)$ = $\dfrac{y}{x}$ … (2)
We know that $cos(2\theta)$ = 2$cos^2(\theta) – 1$
Hence by equation (1) and (2), we can say that
$\Rightarrow$ $\dfrac{y}{x}$ = 2($\dfrac{y}{10}$)^2 – 1
$\Rightarrow$ $50y = x(y^2 – 50)$
Since x, y > 0, therefore $y^2 – 50$ must be positive so y > 7.07
Additionally, in right angles triangle TQS, QT = 10, is the hypotenuse. Hence QS < 10.
Therefore, given that QR = 2y is an integer, the only possible values for y are 7.5, 8, 8.5, 9 and 9.5.
However, only one of these values, at y = 7.5, yields an integral value for PQ = x.
Therefore, we can conclude that y = 7.5 and x = $\dfrac{50*7.5}{7.5^2 – 50}$ = 60.
Hence, the perimeter of $\triangle$PQR = 2x + 2y = 2(60 + 7.5) = 135 units.
44) Answer: 12
We are given that |x-2| = 3
$\Rightarrow$ x = 5, -1
Similarly y = 5, -1
Centre of the square = (2, 2)
Equation of the circle with radius 2 units and centre = (2, 2),
$(x – 2)^2+(y – 2)^2 = 2^2$
$\Rightarrow$ $(x – 2)^2+(y – 2)^2 = 4$
In the graph we can see that ABCD is an square made by lines |x-2| = 3, |y-2| = 3. And a circle of radius 2 cm and centre as (2, 2) is marked in green color.
If we consider only one-fourth part APOQ then there are exactly 3 points with integral coordinates which lie outside the circle but within the square. Hence using symmetry we can say that total 4*3 = 12 points with integral coordinates which lie outside the circle but within the square.
45) Answer (A)
As seen in the earlier qn, the bookstore is the most profitable with a profit of 5060.
46) Answer (B)
Profit for Online=450
The ratio of Online:Supermarket:Bookstore = 3:1:2
Sales for Bookstores = 2/6*60k=20k
Initial C for Bookstores=2/6*39k=13k
Add Cost for Bookstore = 10/275 * 5500+ 30/100*3100 + 9/80*4800 + 9/80*2400 = 200 + 930 + 540 + 270 = 1940.
Profit = 20k-13k-1.94k = 5.06k
Hence, profit of supermarket = 5200 – 5060-450 = -310 (loss). Hence, supermarkets are the least profitable format.
47) Answer (D)
Online format Sales = 50% of 60k = 30k
Online Initial C = 50% of 39k=19.5k
Online Add Cost = 200/275*5500 + 50/100*3100 + 50/80 * 4800 + 50/80*2400 = 4000+ 1550+ 3000+ 1500=10050.
Hence, profit=30k-19.5k-10,050=450. Hence, option D.
48) Answer (D)
When ratio of Income to Expenditure is 6/5, the profit is 20%(6/5 = 1.2)
When ratio of Income to Expenditure is 7/5, the profit is 40%(7/5 = 1.4)
So we need to find the instances in which the profit is between 20% and 40% for the given companies.
For X and Z we see that there are two such instances and for Y, there are 4 such instances. Thus, D is the right choice.
49) Answer (D)
For company X the expenditure on raw materials is equal to the profit in none of the given years.
For company Y, the expenditure on raw materials was equal to the profits in four years 2006, 2007, 2008 and 2010.
For company Z, the expenditure on raw materials was equal to the profits in two years 2007 and 2009.
Thus, in five years , the expenditure on raw materials was equal to the profits.
50) Answer (D)
From formula of profit percent given in the question, the ratio of Expenditures = Ratio of Incomes/Ratio of (100 + profit %)
On observation we can see that 2009 had the highest ratio.