Functions and Inequalities Questions for XAT 2022 – Download PDF

Download Functions and Inequalities Questions for XAT PDF – XAT Functions and Inequalities questions pdf by Cracku. Top 10 very Important Functions and Inequalities Questions for XAT based on asked questions in previous exam papers.

Download Functions and Inequalities Questions for XAT

Get 5 XAT mocks at just Rs.299

Question 1: A function can sometimes reflect on itself, i.e. if y = f(x), then x = f(y). Both of them retain the same structure and form. Which of the following functions has this property?

a) $y=\frac{2x+3}{3x+4}$

b) $y=\frac{2x+3}{3x-2}$

c) $y=\frac{3x+4}{4x-5}$

d) None of the above

Question 2: The total number of onto functions from {1,2,…10} to {1,2,…….9} is

a) $^{10}C_2 \times 9!$

b) $^{10}P_2 \times 9!$

c) $9 \times 10!$

d) $10^9$

Question 3: If n is a positive integer such that $(\sqrt[7]{10})(\sqrt[7]{10})^{2}…(\sqrt[7]{10})^{n}>999$, then the smallest value of n is

Question 4: The number of distinct pairs of integers (m,n), satisfying $\mid1+mn\mid<\mid m+n\mid<5$ is:

Question 5: For a real number x the condition $\mid3x-20\mid+\mid3x-40\mid=20$ necessarily holds it

a) $10<x<15$

b) $9<x<14$

c) $7<x<12$

d) $6<x<11$

XAT 2022 Crash Course

Question 6: $f(x) = \frac{x^2 + 2x – 15}{x^2 – 7x – 18}$ is negative if and only if

a) -5 < x < -2 or 3 < x < 9

b) x < -5 or -2 < x < 3

c) -2 < x < 3 or x > 9

d) x < -5 or 3 < x < 9

Question 7: The number of integers n that satisfy the inequalities $\mid n – 60 \mid < \mid n – 100 \mid < \mid n – 20 \mid$ is

a) 21

b) 19

c) 18

d) 20

Question 8: Find z, if it is known that:
a: $-y^2 + x^2 = 20$
b: $y^3 – 2x^2 – 4z \geq -12$ and
c: x, y and z are all positive integers

a) Any integer greater than 0 and less than 24

b) 24

c) We need one more equation to find z

d) 6

e) 1

Question 9: if x and y are positive real numbers satisfying $x+y=102$, then the minimum possible valus of $2601(1+\frac{1}{x})(1+\frac{1}{y})$ is

Question 10: For real x, the maximum possible value of $\frac{x}{\sqrt{1+x^{4}}}$ is

a) $\frac{1}{2}$

b) $1$

c) $\frac{1}{\sqrt{3}}$

d) $\frac{1}{\sqrt{2}}$

Take XAT 2022 mocks

Answers & Solutions:

1) Answer (B)

Putting y as x and x as y in given options, only options B satisfies the function property as follows.

x = $\frac{2y+3}{3y-2}$

or 3xy – 2x = 2y+3

or y(3x-2) = 2x+3

or $y = \frac{2x+3}{3x-2}$

2) Answer (A)

The number of elements in set A = 10

The number of elements in set B = 9

for the mapping to be onto there will be a element in set B which has 2 pre-images from set A

Two elements can be selected in $^{10}C_2 $ ways and the elements in set B can be arranged in 9! ways

$\therefore$ No of onto functions = $^{10}C_2 \times 9!$

A is the correct answer

3) Answer: 6

$(\sqrt[7]{10})(\sqrt[7]{10})^{2}…(\sqrt[7]{10})^{n}>999$

$(\sqrt[7]{10})^{1+2+…+n}>999$

$10^{\frac{1+2+…+n}{7}}>999$

For minimum value of n,

$\frac{1+2+…+n}{7}=3$

1 + 2 + … + n = 21

We can see that if n = 6, 1 + 2 + 3 + … + 6 = 21.

4) Answer: 12

Let us break this up into 2 inequations [ Let us assume x as m and y as n ]

| 1 + mn | < | m + n |

| m + n | < 5

Looking at these expressions, we can clearly tell that the graphs will be symmetrical about the origin.

Let us try out with the first quadrant and extend the results to the other quadrants.

We will also consider the +X and +Y axes along with the quadrant.

So, the first inequality becomes,

1 + mn < m + n

1 + mn – m – n < 0

1 – m + mn – n < 0

(1-m) + n(m-1) < 0

(1-m)(1-n) < 0

(m – 1)(n – 1) < 0

Let us try to plot the graph.

If we consider only mn < 0, then we get

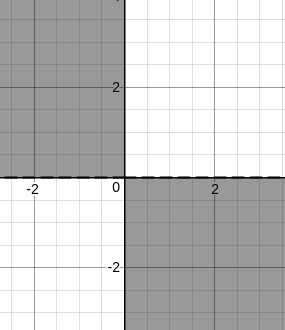
But, we have (m – 1)(n – 1) < 0, so we need to shift the graphs by one unit towards positive x and positive y.

So, we have,

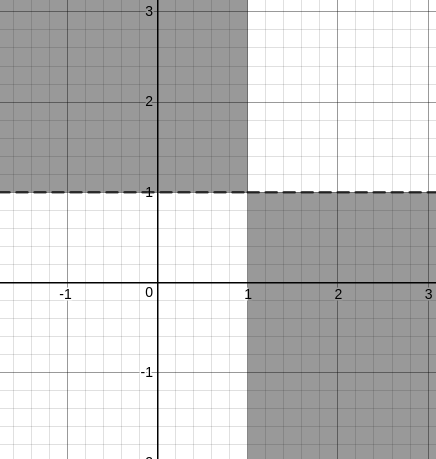
But, we are only considering the first quadrant and the +X and +Y axes. Hence, if we extend, we get the following region.

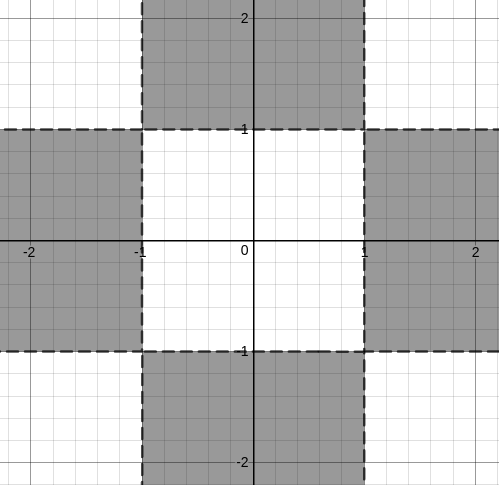
So, if we look for only integer values, we get

(0,2), (0,3),…….

(0,-2), (0, -3),……

(2,0), (3,0), ……

(-2,0), (-3,0), …….

Now, let us consider the other inequation as well, in which |x + y| < 5

Since one of the values is always zero, the modulus of the other value is less than or equal to 4.

Hence, we get

(0,2), (0,3), (0,4)

(0,-2), (0, -3), (0, -4)

(2,0), (3,0), (4,0)

(-2,0), (-3,0), (-4,0)

Hence, a total of 12 values.

5) Answer (C)

Case 1 : $x\ge\frac{40}{3}$
we get 3x-20 +3x-40 =20
6x=80
x=$\frac{80}{6}$=$\frac{40}{3}$=13.33
Case 2 :$\frac{20}{3}\le\ x<\frac{40}{3}\ $
we get 3x-20+40-3x =20
we get 20=20
So we get x$\in\ \left[\frac{20}{3},\frac{40}{3}\right]$
Case 3 $x<\frac{20}{3}$
we get 20-3x+40-3x =20
40=6x
x=$\frac{20}{3}$
but this is not possible
so we get from case 1,2 and 3
$\frac{20}{3}\le\ x\le\frac{40}{3}$
Now looking at options
we can say only option C satisfies for all x .
Hence 7<x<12.

6) Answer (A)

$f(x) = \frac{x^2 + 2x – 15}{x^2 – 7x – 18}$<0

$\frac{\left(x+5\right)\left(x-3\right)}{\left(x-9\right)\left(x+2\right)}<0$

We have four inflection points -5, -2, 3, and 9.

For x<-5, all four terms (x+5), (x-3), (x-9), (x+2) will be negative. Hence, the overall expression will be positive. Similarly, when x>9, all four terms will be positive.

When x belongs to (-2,3), two terms are negative and two are positive. Hence, the overall expression is positive again.

We are left with the range (-5,-2) and (3,9) where the expression will be negative.

7) Answer (B)

We have $\mid n – 60 \mid < \mid n – 100 \mid < \mid n – 20 \mid$.

Now, the difference inside the modulus signified the distance of n from 60, 100, and 20 on the number line. This means that when the absolute difference from a number is larger, n would be further away from that number.

Example: The absolute difference of n and 60 is less than that of the absolute difference between n and 20. Hence, n cannot be $\le\ 40$, as then it would be closer to 20 than 60, and closer on the numeb line would indicate lesser value of absolute difference. Thus we have the condition that n>40.

The absolute difference of n and 100 is less than that of the absolute difference between n and 20. Hence, n cannot be $\le\ 60$, as then it would be closer to 20 than 100. Thus we have the condition that n>60.

The absolute difference of n and 60 is less than that of the absolute difference between n and 100. Hence, n cannot be $\ge80$, as then it would be closer to 100 than 60. Thus we have the condition that n<80.

The number which satisfy the conditions are 61, 62, 63, 64……79. Thus, a total of 19 numbers.

8) Answer (E)

Since $x^2-y^2=20$ and x,y,z are positive integers, the only values possible are x=6 and y=4.

$y^3 – 2x^2 – 4z \geq -12$

Keeping the values of x and y, we get $z\le1$

=> z=1

9) Answer: 2704

Now we have $2601\left(1+\frac{1}{x}\right)\left(1+\frac{1}{y}\right)=2601\left(\frac{xy+y+x+1}{xy}\right)$

Now we know that x+y=102. Substituting it in the above equation

$2601\left(\frac{xy+y+x+1}{xy}\right)=2601\left(\frac{103}{xy}+1\right)$

Maximum value of xy  can be found out by AM>= GM relationship

$\ \frac{\ x+y}{2}\ge\ \sqrt{xy}\ or\ \ \sqrt{\ xy}\le\ 51\ or\ xy\le\ 2601$

Hence the maximum value of “xy” is 2601. Substituting in the above equation we get

$2601\left(\ \frac{\ 103+2601}{2601}\right)=2704$

10) Answer (D)

Now $\frac{x}{\sqrt{\ 1+x^4}}=\ \frac{\ 1}{\sqrt{\ \ \frac{\ 1+x^4}{x^2}}}=\frac{1}{\sqrt{\ \frac{1}{x^2}+x^2}}$

Applying A.M>= G.M.

$\frac{\left(\frac{1}{x^2}+x^2\right)}{2}\ge\ 1\ or\ \ \frac{1}{x^2}+x^2\ge\ 2$ Substituting we get the maximum possible value of the equation as $\frac{1}{\sqrt{\ 2}}$

Download XAT previous papers [PDF]

We hope these Functions and Inequalities questions for XAT pdf for the XAT exam will be highly useful for your preparation.