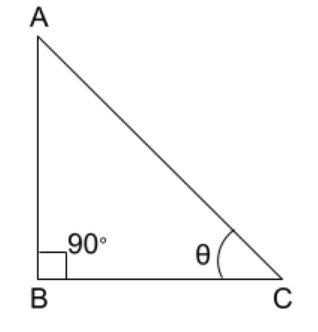
In the above given triangle, AC = Hypotenuse

BC = Base

AB = Height

Here Pythagoras theorem can be used to obtain any of the sides of a triangle with the help of other two sides.

$$(Hypotenuse)^{2} = (Base)^{2} + (Height)^{2}$$

Trigonometric ratios :

Let’s assume Hypotenuse as K, Base as B and Height as L.

Sinθ = $$\frac{L}{K}$$

Cosθ = $$\frac{A}{K}$$

Tanθ = $$\frac{L}{A}$$

Cosecθ = $$\frac{K}{L}$$

Secθ = $$\frac{K}{A}$$

Cotθ = $$\frac{A}{L}$$

$$\frac{Sinθ}{Cosθ} = Tanθ$$

$$\frac{Cosθ}{Sinθ} = Cotθ$$

$$Cosecθ = \frac{1}{Sinθ}$$

$$Secθ = \frac{1}{Cosθ}$$

$$Sin^{2}θ + Cos^{2}θ = 1$$

$$Cosec^{2}θ = 1 + Cot^{2}θ$$

$$Sec^{2}θ = 1 + Tan^{2}θ$$

Sin2θ = 2SinθCosθ

$$Cos2θ = Cos^{2}θ - Sin^{2}θ$$

$$Tan2θ = \frac{2Tanθ}{1-Tan^{2}θ}$$

$$Cot2θ = \frac{Cot^{2}θ-1}{2Cotθ}$$

Sin(A+B) = SinA CosB + SinB CosA

Cos(A+B) = CosA CosB - SinA SinB

$$Tan(A+B) = \frac{Tan A + Tan B}{1 - Tan ATan B}$$

Sin(A-B) = SinA CosB - SinB CosA

Cos(A-B) = CosA CosB + SinA SinB

$$Tan(A-B) = \frac{Tan A - Tan B}{1 + Tan ATan B}$$

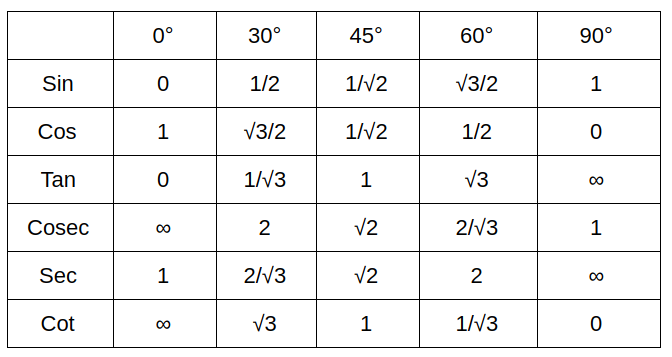
Here 0° to 90° values are given below in the table for the entities.

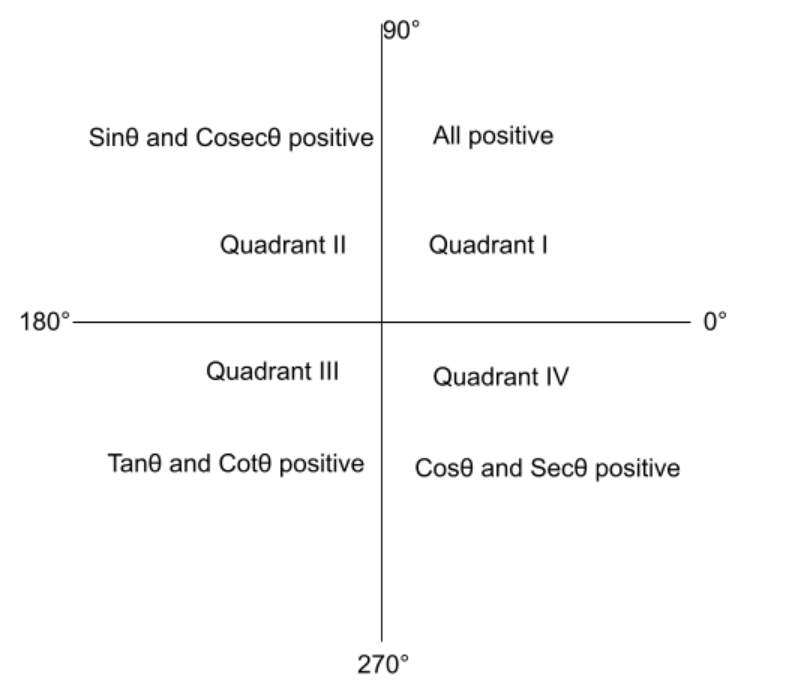
If entities are in the form of (90°+θ), (90°-θ), (270°+θ), (270°-θ), then these will be converted into other forms which are given below.

Sinθ can be changed to Cosθ and reverse of this is also possible.

Cosecθ can be changed to Secθ and reverse of this is also possible.

Tanθ can be changed to Cotθ and reverse of this is also possible.

For other forms like 0°, 180° and 360° entities are not converted.

For example Sin(90°+θ) will be changed to Cosθ.

For example Tan(180°+θ) will be changed to Tanθ.

While converting one entity into another, there is a change in signs during some cases which are given below.