Geometry
‘Geometry and Mensuration’ is a topic from where many questions are asked in SSC exams. It is based on different types of shapes and figures. Shapes are mainly categorized into 2D and 3D. Those shapes which are having two dimensions are called 2D shapes. Those shapes which are having three dimensions are called 3D shapes. In this we have many different formulas through which the area, perimeter and volume of a shape can be calculated.
Square :
Perimeter of a Square = 4 $$\times$$ side of a square
Area of a Square = $$\text{(side of a square)}^{2}$$
Rectangle :
Perimeter of a Rectangle = 2(length+breadth)
Area of a Rectangle = length $$\times$$ breadth
Circle :
Diameter = $$2\times radius$$
Perimeter/Circumference of a Circle = $$2\times\pi\times radius$$
Area of a Circle = $$\pi \times (radius)^{2}$$
Right Angle Triangle:

Perimeter = hypotenuse+base+height
Area = $$\frac{1}{2}\times base \times height$$
Equilateral Triangle:
Perimeter = 3a
Area = $$\frac{\sqrt{3}}{4}\times a^{2}$$
Isosceles Triangle:
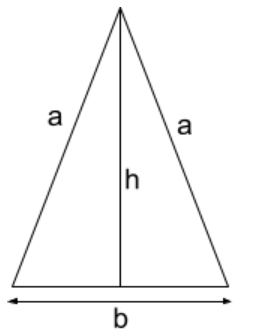
Perimeter = (2a+b)
Area = $$\frac{1}{2}\times b \times h$$
Scalene Triangle:
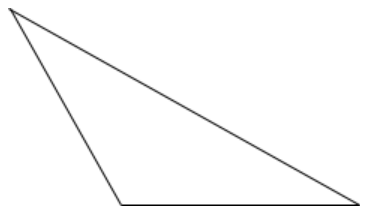
Perimeter = (a+b+c)
S = (a+b+c)/2
Area = $$\sqrt{S(S-a)(S-b)(S-c)}$$
Here a, b and c are the three sides of a triangle.
Note :: The sum of all the three angles of a triangle is equal to 180°.
Rhombus:
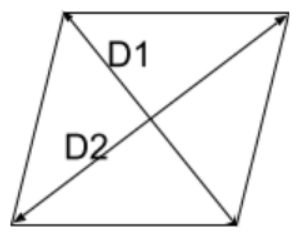
Perimeter = 4 $$\times$$ side
Area = $$\frac{1}{2}\times D_{1} \times D_{2}$$
Parallelogram:
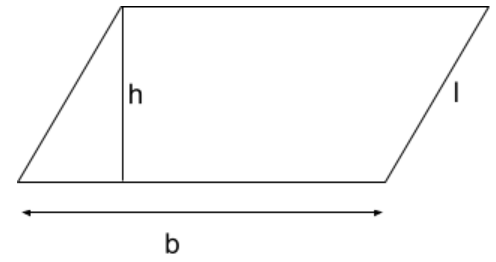
Perimeter = $$2\times(l+b)$$
Area = $$b \times h$$
Trapezium:
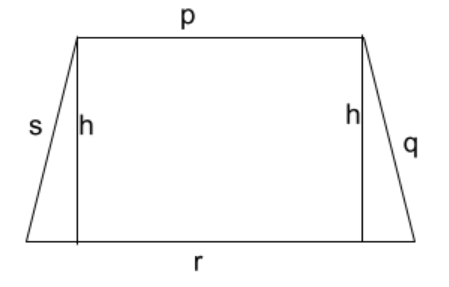
Perimeter = p+q+r+s
Area = $$\frac{1}{2}\times h \times(p+r)$$
Cube:
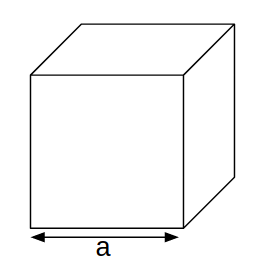
Curved surface area = $$4 \times a^{2}$$
Total surface area = $$6 \times a^{2}$$
Volume = $$a^{3}$$
Cuboid:
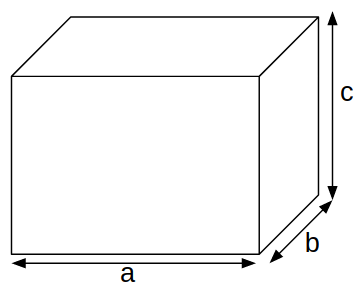
Curved(lateral) surface area = 2c(a+b)
Total surface area = 2(ab+bc+ca)
Volume = $$a \times b \times c$$
Sphere:
Curved(lateral) surface area = $$4\times\pi\times (radius)^{2}$$
Total surface area = $$4\times\pi\times (radius)^{2}$$
Volume = $$\frac{4}{3} \times\pi\times (radius)^{3}$$
Hemisphere:
Curved(lateral) surface area = $$2\times\pi\times (radius)^{2}$$
Total surface area = $$3\times\pi\times (radius)^{2}$$
Volume = $$\frac{2}{3} \times\pi\times (radius)^{3}$$
Cylinder:
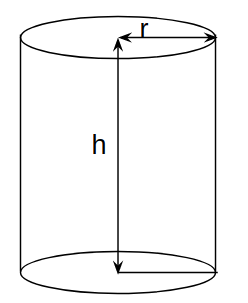
Here r = radius
h = height
Curved(lateral) surface area = $$2\times\pi\times r \times h$$
Total surface area = $$2\times \pi \times r \times (r+h)$$
Volume = $$\pi \times r^{2} \times h$$
Cone:
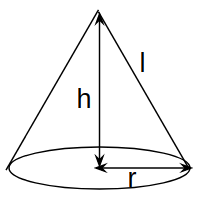
Here r = radius
h = height
l = slant height
$$l^{2} = r^{2}+h^{2}$$
Curved(lateral) surface area = $$\pi\times r \times l$$
Total surface area = $$\pi\times r \times (r+l)$$
Volume = $$\frac{1}{3}\times\pi \times r^{2}\times h$$
Q) If the volume of a hemisphere is 155232 $$cm^{3}$$, then find out the curved surface area of the hemisphere.
Sol.
volume of a hemisphere = 155232
$$\frac{2}{3} \times\pi\times (radius)^{3} = 155232$$
$$\frac{2}{3} \times \frac{22}{7} \times (radius)^{3} = 155232$$
$$ \frac{44}{21} \times (radius)^{3} = 155232$$
$$(radius)^{3} = 74088$$
radius = 42 cm
Curved surface area of a hemisphere = $$2\times\pi\times (radius)^{2}$$
= $$2\times\frac{22}{7}\times (42)^{2}$$
= $$44 \times 42 \times 6$$
= 11088 $$cm^{2}$$
Q) If the radius and height of a cone is 24 cm and 10 cm respectively, then find out the total surface area of the cone.
Sol.
$$l^{2} = r^{2}+h^{2}$$
$$l^{2} = 24^{2}+10^{2}$$
$$l^{2} = 576+100$$
$$l^{2} = 676$$
l = 26 cm
Total surface area of the cone = $$\pi\times r \times (r+l)$$
= $$\pi\times 24 \times (24+26)$$
= $$\pi\times 24 \times 50$$
= 1200 $$\pi$$ $$cm^{2}$$
