XAT Graphs Questions [Download PDF]
Graphs is an important topic in the Quant section of the SNAP Exam. Quant is a scoring section in XAT, so it is advised to practice as much as questions from quant. This article provides some of the most important Graphs Questions for XAT. One can also download this Free Graphs Questions for XAT PDF with detailed answers by Cracku. These questions will help you practice and solve the Graphs questions in the XAT exam. Utilize this PDF practice set, which is one of the best sources for practicing.
Download Graphs Questions for XAT
Enroll to XAT 2023 Crash Course
Question 1: Let r be a real number and $f(x) = \begin{cases}2x -r & ifx \geq r\\ r &ifx < r\end{cases}$. Then, the equation $f(x) = f(f(x))$ holds for all real values of $x$ where
a) $x > r$
b) $x \leq r$
c) $x \neq r$
d) $x \geq r$
1) Answer (B)
Solution:
When x< r
f(x) = r
f(x) = f(f(x))
r = f(r)
r= 2r-r
r=r
When x>=r
f(x) = 2x-r
f(x) = f(f(x))
2x-r = f(2x-r)
2x-r = 2(2x-r) – r
2x-r = 4x-3r
or, x=r
Therefore x<= r
Question 2: Suppose for all integers x, there are two functions f and g such that $f(x) + f (x – 1) – 1 = 0$ and $g(x ) = x^{2}$. If $f\left(x^{2} – x \right) = 5$, then the value of the sum f(g(5)) + g(f(5)) is
2) Answer: 12
Solution:
Given,
$f\left(x\right)+f\left(x-1\right)=1$ …… (1)
$f\left(x^2-x\right)=5$ …… (2)
$g\left(x\right)=x^2$
Substituting x = 1 in (1) and (2), we get
f(0) = 5
f(1) + f(0) = 1
f(1) = 1 – 5 = -4
f(2) + f(1) = 1
f(2) = 1 + 4 = 5
f(n) = 5 if n is even and f(n) = -4 if n is odd
f(g(5)) + g(f(5)) = f(25) + g(-4) = -4 + 16 = 12
Question 3: Let $f(x)$ be a quadratic polynomial in $x$ such that $f(x) \geq 0$ for all real numbers $x$. If f(2) = 0 and f( 4) = 6, then f(-2) is equal to
a) 12
b) 24
c) 6
d) 36
3) Answer (B)
Solution:
$f(x) \geq 0$for all real numbers $x$, so D<=0
Since f(2)=0 therefore x=2 is a root of f(x)
Since the discriminant of f(x) is less than equal to 0 and 2 is a root so we can conclude that D=0
Therefore f(x) = $a\left(x-2\right)^2$
f(4)=6
or, 6 = $a\left(x-2\right)^2$
a= 3/2
$f\left(-2\right)=\ -\frac{3}{2}\left(-4\right)^2=24$
Question 4: For any real number x, let [x] be the largest integer less than or equal to x. If $\sum_{n=1}^N \left[\frac{1}{5} + \frac{n}{25}\right] = 25$ then N is
4) Answer: 44
Solution:
It is given,
$\Sigma_{n=1}^N\ \left[\frac{1}{5}+\frac{n}{25}\right]=25$
$\Sigma_{n=1}^N\ \left[\frac{5+n}{25}\right]=25$
For n = 1 to n = 19, value of function is zero.
For n = 20 to n = 44, value of function will be 1.
44 = 20 + n – 1
n = 25 which is equal to given value.
This implies N = 44
Question 5: Let $0 \leq a \leq x \leq 100$ and $f(x) = \mid x – a \mid + \mid x – 100 \mid + \mid x – a – 50\mid$. Then the maximum value of f(x) becomes 100 when a is equal to
a) 25
b) 100
c) 50
d) 0
5) Answer (C)
Solution:
x>=a, so |x-a| = x-a
x<100, so |x-100| = 100-x
f(x) = (x-a) + (100-x) + |x-a-50| =100
or, |x-a-50| = a

From the graph we can can see that when x=a then
|x-a-50|=a
or, a= 50
Similarly when x=a+100
|x-a-50|=a
or, a= 50
So value of a is 50 when f(x) is 100.
Take SNAP mock tests here
Enrol to 10 SNAP Latest Mocks For Just Rs. 499
Question 6: Given below are two statements:
Statement I : The set of numbers (7,8,9,a,b,10,8,7) has an arithmetic mean of 9 and mode(most frequently occurring number) as 8, Then a x b = 120.
Statement II : Let a and b be two positive integers such that a + b + a x b = 84, then a + b =20.
In the light of the above statements, choose the most appropriate answer from the options given below
a) Both Statement I and Statement II are correct
b) Both Statement I and Statement II are incorrect
c) Statement I is correct but Statement II is incorrect
d) Statement I is incorrect but Statement II is correct
6) Answer (A)
Solution:
Statement I:
Given arithmetic mean of (7,8,9,a,b,10,8,7) is 9 and mode is 8
7+8+9+a+b+10+8+7 = $9\times\ 8$
49+a+b = 72
a+b = 23
It is mentioned that mode is 8, 8 occurred twice and 7 also occurred twice. Therefore, a or b should be 8
If a = 8, b = 15
If b = 8, a = 15
ab = 120
Statement I is true
Statement II:
a + b + ab = 84
1 + a + b + ab = 85
(1+a)(1+b) = 85
85 = 1 $\times\ $ 85 or 5 $\times\ $ 17
It cannot be 1$\times\ $85, as it is mentioned both a and b are positive integers
If 1+a = 5, 1+b = 17
a =4 and b = 16
If 1+a = 17, 1+b = 5
a = 16 and b = 4
In both cases, a+b = 20
Statement II is true
Answer is option A.
Question 7: The following observations are arranged in ascending order: 26, 29, 42, 53, X, X+2, X+5, 75, 82, 93: If the median is 65; Find the value of X.
a) 70
b) 55
c) 64
d) 58
7) Answer (C)
Solution:
There are even number of observations in the given data. Therefore, median is the average of X and X+2.
$\ \frac{\ X+X+2}{2}=65$
X + 1 = 65
X = 64
Answer is option C.
Question 8: $f(x) = \frac{2x + 2}{2x – 2}$, where y = f(x). Find the ratio of x to f(y).
a) $\sqrt{x} : \sqrt{y}$
b) $x^3 : y^3$
c) 1 : 2
d) 1 : 1
8) Answer (D)
Solution:
$f\left(y\right)=f\left(f\left(x\right)\right)$
or, $f\left(y\right)=f\left(\frac{2x+2}{2x-2}\right)$
$f\left(y\right)=\frac{2\left(\frac{2x+2}{2x-2}\right)+2}{2\left(\frac{2x+2}{2x-2}\right)-2}$
or, $f\left(y\right)=\frac{8x}{8}=x$
Therefore x:f(y) = 1:1
Question 9: If $f(x)=x^{2}-7x$ and $g(x)=x+3$, then the minimum value of $f(g(x))-3x$ is:
a) -20
b) -12
c) -15
d) -16
9) Answer (D)
Solution:
Now we have :
$f(g(x))-3x$
so we get f(x+3)-3x
= $\left(x+3\right)^2-7\left(x+3\right)-3x$
=$x^2-4x-12$
Now minimum value of expression = $-\frac{D}{4a}$ $ \frac{\left(4ac-b^2\right)}{4a}$
We get – (16+48)/4
= -16
Question 10: Two sets AA and BB are defined as follows:-
$AA = \left\{x \mid x \in N, x < 5\right\}$
$AA = \left\{x \mid x \in N, x2 < 25\right\}$, n(XX) = number of elements in XX. Choose the CORRECT option.
a) n(AA) > n(BB)
b) n(AA) < n(BB)
c) AA = BB
d) n(AA) $\leq$ n(BB)
10) Answer (C)
Solution:
AA= {1, 2, 3, 4}; n(AA)= 4
BB= {1, 2, 3, 4}; n(BB)=4
So, AA=BB
Question 11: Let $g(x)+g(\frac{1}{x})=1+3x$. Find the value of $g(3)$.
a) $-4$
b) $-\frac{1}{2}$
c) $\frac{1}{2}$
d) $3$
11) Answer (E)
Solution:
The question appeared in CMAT 2021 Slot 2 and the question is incorrect . Marks were awarded to students.
Question 12: Which of the following equations best describes the graph given below?

a) $\mid x+y\mid-\mid x-y\mid=6$
b) $\mid x-y\mid+\mid x+y\mid=10$
c) $\mid x\mid-\mid y\mid=6$
d) $\mid x+y\mid-\mid x-y\mid=0$
12) Answer (C)
Solution:
In these type of questions
we go through the options :
Now when x=6 or -6 the value of y is 0
so let us put value of y=0 in all options and check which option satisfies x=6 and -6
Putting x=6 and y=0 in option A
we get |6+0|-|6-0| = 0
But RHS =6 so this option is discarded
Now putting in option B
|6-0|+|6+0| =12
But RHS is 10
so this option is also discarded .
Now option C we get
|6|-0 =6
so we can say graph can be of |x|-|y|=6
Now satisfying option D
we get |6+0|-|6-0|=0
So we can say 6,0 and -6,0 satisfies option D as well
Now you have to eliminate between C and D
If you observe |x+y|-|x-y|=0 will pass through origin
and the graph here is not passing through origin so you can eliminate option D
Therefore the graph will be |x|-|y|=6
Question 13: Which of the following graphs represent the function of x?




Choose the correct answer from the options given below :
a) (A), (B) and (C) only
b) (A), (B) and (D) only
c) (A) and (D) only
d) (A) and (C) only
13) Answer (C)
Solution:
Graph A and D represent the function of x, because a vertical line is drawn in (a) meets the graph at only one point i.e., for one x, in the domain there exist only one f(x) in the codomain.
Question 14: In how many ways can a pair of integers (x , a) be chosen such that $x^{2}-2\mid x\mid+\mid a-2\mid=0$ ?
a) 6
b) 5
c) 4
d) 7
14) Answer (D)
Solution:
$x^{2}-2\mid x\mid+\mid a-2\mid=0$
where x>= 0 and x>=2
$x^2-2x+a-2\ =0$ Using quadratic equation we have $x=\ 1+\sqrt{\ 3-a}\ and\ x=1-\sqrt{\ 3-a}$ Only two integer values are possible
a=2 and a=3. So corresponding “x” values are x=1 and a=3, x=2 and a=2, x=0 and a=2
where x>=0 and x<2
Applying the above process we get x=1 and a=1
where x<0 and x>=2 we get a=3 and x=-1 , a=2 and x=-2
where x<0 and x<2 we get a=1 and x=-1
Hence there are total 7 values possible
Question 15: In a group of 10 students, the mean of the lowest 9 scores is 42 while the mean of the highest 9 scores is 47. For the entire group of 10 students, the maximum possible mean exceeds the minimum possible mean by
a) 5
b) 4
c) 3
d) 6
15) Answer (B)
Solution:
Let x(1) be the least number and x(10) be the largest number. Now from the condition given in the question , we can say that
x(2)+x(3)+x(4)+……..x(10)= 47*9=423……………….(1)
Similarly x(1)+x(2)+x(3)+x(4)…………….+x(9)= 42*9=378……………(2)
Subtracting both the equations we get x(10)-x(1)=45
Now, the sum of the 10 observations from equation (1) is 423+x(1)
Now the minimum value of x(10) will be 47 and the minimum value of x(1) will be 2 . Hence minimum average 425/10=42.5
Maximum value of x(1) is 42. Hence maximum average will be 465/10=46.5
Hence difference in average will be 46.5-42.5=4 which is the correct answer
Question 16: Let $f(x)=x^{2}+ax+b$ and $g(x)=f(x+1)-f(x-1)$. If $f(x)\geq0$ for all real x, and $g(20)=72$. then the smallest possible value of b is
a) 16
b) 4
c) 1
d) 0
16) Answer (B)
Solution:
$f\left(x\right)=\ x^2+ax+b$
$f\left(x+1\right)=x^2+2x+1+ax+a+b$
$f\left(x-1\right)=x^2-2x+1+ax-a+b$
$ g(x)=f(x+1)-f(x-1)= 4x+2a$
Now $g(20) = 72$ from this we get $a = -4$ ; $f\left(x\right)=x^2-4x\ +b$
For this expression to be greater than zero it has to be a perfect square which is possible for $b\ge\ 4$
Hence the smallest value of ‘b’ is 4.
Question 17: If $f(x+y)=f(x)f(y)$ and $f(5)=4$, then $f(10)-f(-10)$ is equal to
a) 14.0625
b) 0
c) 15.9375
d) 3
17) Answer (C)
Solution:
The given function is equivalent to f(x) = $a^x$
Given, f(5) = 4
=> $a^5=4=>\ a=4^{\frac{1}{5}}$
=> f(x) = $4^{\frac{x}{5}}$
f(10) – f(-10) = 16 – 1/16 = 15.9375
Question 18: The area, in sq. units, enclosed by the lines $x=2,y=\mid x-2\mid+4$, the X-axis and the Y-axis is equal to
a) 10
b) 6
c) 8
d) 12
18) Answer (A)
Solution:
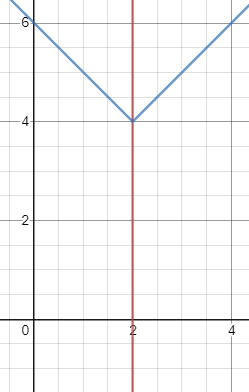
The required figure is a trapezium with vertices A(0,0), B(2,0), C(2,4) and D(0,6)
AB = 2 BC = 4 and AD = 6
Area of trapezium = $\frac{1}{2}\left(sum\ of\ the\ opposite\ sides\right)\cdot height$ = $\frac{1}{2}\left(4+6\right)\cdot2\ =\ 10$
Question 19: If $f(5+x)=f(5-x)$ for every real x, and $f(x)=0$ has four distinct real roots, then the sum of these roots is
a) 0
b) 40
c) 10
d) 20
19) Answer (D)
Solution:
Let ‘r’ be the root of the function. It follows that f(r) = 0. We can represent this as $f\left(r\right)=f\left\{5-\left(5-r\right)\right\}$
Based on the relation: $f\left(5-x\right)=f\left(5+x\right)$; $f\left(r\right)=f\left\{5-\left(5-r\right)\right\}=f\left\{5+\left(5-r\right)\right\}$
$\therefore\ f\left(r\right)=f\left(10-r\right)$
Thus, every root ‘r’ is associated with another root ‘(10-r)’ [these form a pair]. For even distinct roots, in this case four, let us assume the roots to be as follows: $r_1,\ \left(10-r_1\right),\ r_2,\ \left(10-r_2\right)$
The sum of these roots = $r_1\ +\left(10-r_1\right)+\ r_2+\ \left(10-r_2\right)\ =\ 20$
Hence, Option D is the correct answer.
Question 20: The area of the region satisfying the inequalities $\mid x\mid-y\leq1,y\geq0$ and $y\leq1$ is
20) Answer: 3
Solution:
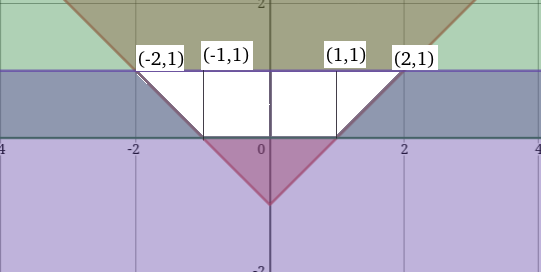
The area of the region contained by the lines $\mid x\mid-y\leq1,y\geq0$ and $y\leq1$ is the white region.
Total area = Area of rectangle + 2 * Area of triangle = $2+\left(\frac{1}{2}\times\ 2\times\ 1\right)\ =3$
Hence, 3 is the correct answer.





