Venn Diagrams Questions for XAT

Venn Diagrams Questions for XAT

Download important Venn Diagrams Questions for XAT PDF based on previously asked questions in the XAT exam. Practice Venn Diagrams Questions PDF for XAT exam.

Download Venn Diagrams Questions for XAT PDF

Get 5 XAT mocks for Rs. 299. Enroll here

Instructions

There were a hundred schools in a town. Of these, the number of schools having a play – ground was 30, and these schools had neither a library nor a laboratory. The number of schools having a laboratory alone was twice the number of those having a library only. The number of schools having a laboratory as well as a library was one-fourth the number of those having a laboratory alone. The number of schools having either a laboratory or a library or both was 35.

Question 1: What was the ratio of schools having laboratory those having library?

a) 1 : 2

b) 5 : 3

c) 2 : 1

d) 2 : 3

Question 2: In a locality, two-thirds of the people have cable TV, one-fifth have VCR, and one-tenth have both. What is the fraction of people having atleast one among cable -TV and VCR?

a) $\frac{19}{30}$

b) $\frac{2}{3}$

c) $\frac{17}{30}$

d) $\frac{23}{30}$

Question 3: In the census of the men of a village was conducted and the following results were obtained: n(not businessmen) = 350, n(businessmen) = 30% of total men. It is also known that married businessmen and single men not doing business combined make 50% of the total male population. Find the maximum number of married men not engaged in business.

a) 120

b) 150

c) 250

d) 100

Question 4: In a class of 100 students, 60 students got an interview call from IIMA, 70 students got a call from IIMB, 80 students got a call from IIMC. If X and Y are the minimum and maximum number of students who received atleast two calls. What is the value of X+Y?

a) 145

b) 155

c) 180

d) 160

Question 5: In a class of 100 students, the number of students who like chocolates is at least five times the number of students who like biscuits. If each student likes atleast a chocolate or a biscuit, then the minimum number of students who like chocolates is

Question 6: The figure given below depicts the number of children who like various fruits.

Find the number of children who like at least 3 fruits.

XAT Solved Previous papers

Take XAT Mock Test

Question 7: Among the first year students of IIM Calicut, 100 students do not like DC comics and 134 students do not like Marvel comics. If the difference between the students who like both and the number of students who like none is 24, how many students like only one out of the two comics?

a) 200

b) 198

c) 186

d) Cannot be determined

Question 8: 290 students of MBA (International Business) in a reputed Business School have to study foreign language in Trimesters IV and V. Suppose the following information are given .
i. 120 students study Spanish
ii. 100 students study Mandarin
iii. At least 80 students, who study a foreign language, study neither Spanish nor Mandarin
Then the number of students who study Spanish but not Mandarin could be any number from

a) 80 to 170

b) 80 to 100

c) 50 to 80

d) 20 to 110

Question 9: A survey was conducted of 100 people to find out whether they had read recent issues of Golmal, a monthly magazine. The summarized information regarding readership in 3 months is given below:Only September: 18;September but not August: 23;September and July: 8;September:28;July: 48;July and August: 10;none of the three months: 24What is the number of surveyed people who have read exactly two consecutive issues (out of the three)?

a) 7

b) 9

c) 12

d) 14

e) 17

Instructions

DIRECTIONS for the following two questions: Answer the questions on the basis of the information given below.

New Age Consultants have three consultants Gyani, Medha and Buddhi. The sum of the number of projects handled by Gyani and Buddhi individually is equal to the number of projects in which Medha is involved. All three consultants are involved together in 6 projects. Gyani works with Medha in 14 projects. Buddhi has 2 projects with Medha but without Gyani, and 3 projects with Gyani but without Medha. The total number of projects for New Age Consultants is one less than twice the number of projects in which more than one consultant is involved.

Question 10: What is the number of projects in which Gyani alone is involved?

a) Uniquely equal to zero.

b) Uniquely equal to 1.

c) Uniquely equal to 4.

d) Cannot be determined uniquely.

XAT Decision making practice questions

Answers & Solutions:

1) Answer (B)

The diagram for this question has been shown:

Total number of schools having either or LAB or LIB or both = a+b+x/2 – y + y + 3x = 7x/2 + a + b = 35

It has been given that the schools having playground don’t have a Library or Laboratory.

Hence  a = b = y = 0

7x/2 = 35

x = 10

Required ratio = 25:15 = 5:3

2) Answer (D)

Let the distribution of people having cable TV and VCR be as given in the diagram above.
Hence, $a+c =\frac{2}{3}$
$b+c=\frac{1}{5}$
and $c=\frac{1}{10}$

We need to find $a+b+c=?$
This equals $(a+b)+(b+c)-c = \frac{2}{3}+\frac{1}{5}-\frac{1}{10}$
Which equals $\frac{20+6-3}{30}=\frac{23}{30}$

3) Answer (C)

Let us draw the venn diagram of the given situation :

From the information give, we know that

$c+d=350$ — (1)

$a+b=\dfrac{3}{10} \times (a+b+c+d)$ —-(2)

Putting value of equation (1) in equation (2)

$a+b = \dfrac{3}{10} \times (a+b+350)$

$a+b(1- \dfrac{3}{10}) = 105 $

$a+b = \dfrac{105}{\dfrac{7}{10}} $

$a+b= 150$ —–(3)

Thus, total men = 350 + 150 = 500

Also, $b+d = \dfrac{1}{2} \times (a+b+c+d) $

$ \Rightarrow b+d = \dfrac{1}{2} \times 500 $

$ \Rightarrow b+d = 250 $ — (4)

Putting value of $d$ from equation (1) in equation (4),

$ b + 250 – c = 250 $

$ \Rightarrow c – b = 100 $

$ \Rightarrow c = b+100 $

Now, from equation (3) and equation (4), we know

$ b = 150 – a $ and $ b = 250-d $

Thus, the maximum value of $b$ possible is 150 (assuming $a$=0).

We cannot assume $d$=0 because in that case $a+b >150$

Thus, maximum value of $c_{max} = 150+100 = 250$

4) Answer (B)

Let us consider I, II, III be the number of students who got calls from one, two, three institutes respectively.
x be the number of students who got calls from none of the three institutes
I+II+III+x=100
I+2*II+3*III=60+70+80=210
Case 1. If we want to minimize the number of students who received calls from atleast two institute we have to maximize the students who received calls from only one institute but there are 210 calls and students are 100. Hence we have to consider maximum students got selected in all three institutes and none of the student got call exactly two institute.
number of students who got calls from two institutes (II)=0

I+III=100
I+3*III=210

By solving the above two equations we get III= 55 and I=45.

Thus the minimum number of students who received atleast two calls X = 55
In the figure given below a+b+c= 45

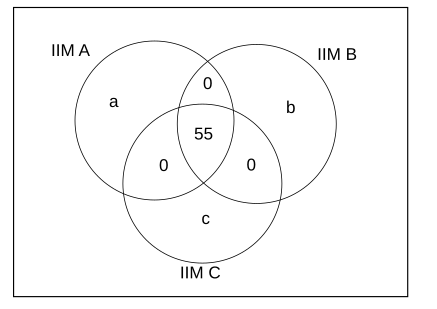
Number of students who received calls from IIM A = 60

a+55=60      $\therefore$ a = 5

Number of students who received calls from IIM B = 70

b+55=70      $\therefore$ b = 15

Number of students who received calls from IIM C = 80

c+55=80       $\therefore$ c = 25

 

Case 2. If we want to maximize the number of students who received calls from atleast two institute we have to maximize the students who received calls from exactly two institute. Suppose all the students got selected in exactly two institutes then the number of calls must be 200. The number of calls is 210, then few students must have three calls. The number of students who get calls from only one institute must be 0.

We can definitely say that all the students got call from atleast 2 institutes.

2II+3III=210

II+III=100

By solving the above two equations we get III= 10 and II=90.

In the table given below a+b+c=90

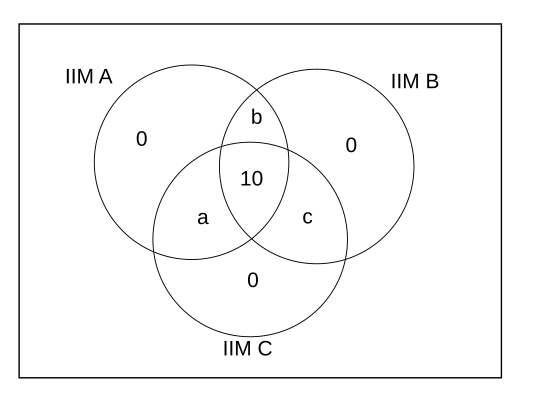
Number of students who received calls from IIM A = 60

a+b+10=60

Number of students who received calls from IIM B = 70

b+c+10=70

Number of students who received calls from IIM C = 80

a+c+10=80

a+b+c=90

a=30, b=20, c=40

The maximum number of students who will receive calls from at least two institutes Y =100

Sum X+Y =55+100=155

B is the correct answer.

XAT Quant formulas PDF

Take XAT Mock Test

5) Answer: 84

Let the number of students who like biscuits be B

Let the number of students who like chocolates be C

Let the number of students who like both be X (X $\geq$ 0)

So, the number of students who like only biscuits is B-X and the number of students who like only chocolates be C-X

As C $\geq$ 5*B, let C = 5B+K where K is a whole number.

As the total number of students equals 100, therefore, (B-X) + (C-X) + X = 100 or B+C-X = 100

Therefore, C + (C-K)/5 – X = 100

Or, 6C/5 = 100 + X + K/5

Or C = 83.33 + 5X/6 + K/6

As, both X and K are non negative, C $\geq$ 83.33. But as C is a whole number, the minimum value of C is 84. In this case, B can be 16 and X is 0.

6) Answer: 38

3 students like Apple,Orange and Kiwi. 35 students like Kiwi, Mango and Orange

Hence $35+3=38$ is the correct answer.

7) Answer (D)

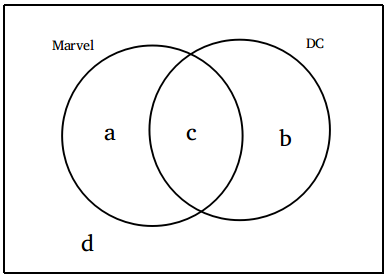
100 students do not like DC comics. So, a + d = 100 ……….(i)

134 students do not like Marvel comics. So, b + d = 134 …….(ii)

Difference between the number of students who like both and the number of students who like none is 24.

=> |c – d| = 24 ………(iii)

Adding (i), (ii) and (iii), we get

a + b + c + d = 258 …….(iv)

a + c + 3d – b =258 …….(v)

We have to find the value of (a + b)

By using these equations, we cannot find the value of (a + b).

Thus, the answer cannot be determined,

Hence, option D is the correct answer.

 

8) Answer (D)

                                                                

It’s given that 120 students study Spanish :         A + B = 120                                        …(1)

Also 100 students study Mandarin :       B + C = 100                                        …(2)

At least 80 students will not opt for any of these two languages i.e.

Spanish + Mandarin $\leq$ (290-80)

Spanish + Mandarin $\leq$ 210

A + B + C $\leq$ 210

Case 2: When B is minimum and A is maximum.

Solving for boundary condition  A + B + C = 210                                                             …(3)

Solving equations (1)+(2)-(3)

B = 10

i.e. A = 120 – B = 120 – 10 =110 {Maximum possible value of A}

Case 2: When B is maximum and A is minimum.

Since B+C = 100 so, Maximum value B can attain is 100. Hence, the minimum value of A = 120 – B = 120 – 100 = 20 {Minimum possible value of A}

So we can say that the number of students who study Spanish but not Mandarin will be A [20 ,110].

9) Answer (B)

Let the areas be labelled as shown in the diagram above.

The number of people corresponding to “none of the three months” is 24. So, H is 24.

Only September is 18. So, G = 18

September but not August is 23. So, G + D = 23.

Hence, D = 23 – 18 = 5.

We know that September and July is 8. So, D + E = 8

This implies E = 3.

September = 28. So, D + E + F + G = 28.

So, F = 28 – 5 – 3 – 18 = 2.

July and August = 10.

So, B + E = 10.

E = 3. So, B = 7.

July = 48.

So, A + B + D + E = 48

A = 48 – 7 – 5 – 3 = 33.

There are 100 people in total. So, C = 100 – A – B – D – E – F – G – H = 100 – 33 – 7 – 5 – 3 – 2 – 18 – 24 = 8

So, number of people who read exactly two consecutive issues = (July & August) + (August & September) = B + F = 7 + 2 = 9

10) Answer (D)

The total number of projects = 2(3+6+8+2) – 1 = 38 – 1 = 37
So, 19 + 2(x+y) – 16 = 37
=> x+y = 17
The number of projects in which Medha alone is involved is 17-16 = 1
But the number of projects in which Gyani alone is involved cannot be uniquely determined

XAT Solved Previous papers

Take XAT Mock Test

We hope this Venn Diagrams  Questions PDF for XAT with Solutions will be helpful to you.