Time, Speed and Distance Questions for XAT

Download important Time, Speed and Distance Questions for XAT PDF based on previously asked questions in XAT exam. Practice Time, Speed and Distance Questions PDF for XAT exam.

Download Time, Speed and Distance Questions for XAT

Get 5 XAT mocks for Rs. 299. Enroll here

Instructions

Directions for the following two questions: Cities A and B are in different time zones. A is located 3000 km east of B. The table below describes the schedule of an airline operating non-stop flights between A and B. All the times indicated are local and on the same day.

Assume that planes cruise at the same speed in both directions. However, the effective speed is influenced by a steady wind blowing from east to west at 50 km per hour.

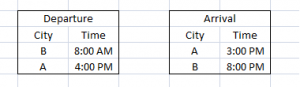
Question 1: What is the time difference between A and B?

a) 1 hour and 30 minutes

b) 2 hours

c) 2 hours and 30 minutes

d) 1 hour

e) Cannot be determined

Question 2: It takes six technicians a total of 10 hr to build a new server from Direct Computer, with each working at the same rate. If six technicians start to build the server at 11 am, and one technician per hour is added beginning at 5 pm, at what time will the server be completed?

a) 6.40 pm

b) 7 pm

c) 7.20 pm

d) 8 pm

Question 3: Three small pumps and a large pump are filling a tank. Each of the three small pump works at 2/3 the rate of the large pump. If all four pumps work at the same time, they should fill the tank in what fraction of the time that it would have taken the large pump alone?

a) 4/7

b) 1/3

c) 2/3

d) 3/4

Question 4: Three machines, A, B and C can be used to produce a product. Machine A will take 60 hours to produce a million units. Machine B is twice as fast as Machine A. Machine C will take the same amount of time to produce a million units as A and B running together. How much time will be required to produce a million units if all the three machines are used simultaneously?

a) 12 hours

b) 10 hours

c) 8 hours

d) 6 hour

Question 5: In a watch, the minute hand crosses the hour hand for the third time exactly after every 3 hr 18 min and 15s of normal time. What is the time gained or lost by this watch in one day?

a) 14 min 10 s lost

b) 13 min 48 s lost

c) 13 min 20 s gained

d) 14 min 40 s gained

Question 6: Two boats, traveling at 5 and 10 kms per hour, head directly towards each other. They begin at a distance of 20 kms from each other. How far apart are they (in kms) one minute before they collide.

a) 1/12

b) 1/6

c) 1/4

d) 1/3

Question 7: On a 20 km tunnel, connecting two cities A and B, there are three gutters (1, 2 and 3). The distance between gutters 1 and 2 is half the distance between gutters 2 and 3. The distance from city A to its nearest gutter, gutter 1, is equal to the distance of city B from gutter 3. On a particular day, the hospital in city A receives information that an accident has happened at gutter 3. The victim can be saved only if an operation is started within 40 min. An ambulance started from city A at 30 km/hr and crossed gutter 1 after 5 min. If the driver had doubled the speed after that, what is the maximum amount of time would the doctor get to attend the patient at the hospital. Assume 1 min is elapsed for taking the patient into and out of the ambulance?

a) 4 min

b) 2.5 min

c) 1.5 min

d) The patient died before reaching the hospital

XAT Solved Previous papers

Take XAT Mock Test

Question 8: A train approaches a tunnel AB. Inside the tunnel is a cat located at a point that is 3/8 of the distance AB measured from the entrance A. When the train whistles the cat runs. If the cat moves to the entrance of the tunnel A, the train catches the cat exactly at the entrance. If the cat moves to the exit B, the train catches the cat at exactly the exit. What is the ratio of speed of train and cat ?

a) 3 : 1

b) 4 :1

c) 5 : 1

d) None of these

Question 9: City Bus Corporation runs two buses from terminus A to terminus B,one from each of the terminuses such that each bus makes 5 round trips in a day. There are no stops in between. These buses ply back and forth on the same route at different but uniform speeds. Each morning the buses start at 7 AM from the respective terminuses. They meet for the first time at a distance of 7 km from terminus A. Their next meeting is at a distance of 4 km from terminus B, while travelling in opposite directions. Assuming that the time taken by the buses at the terminuses is negligibly small, and the cost of running a bus is 20 per km, find the daily cost of running the buses (in )

a) 3200

b) 6800

c) 4000

d) 6400

e) None of the above

Question 10: A ping pong ball is dropped from a 45 metres high multi-storey building. The ball bounces back three fifth of the distance each time before coming to rest. The total distance traversed by the ball is:

a) 150 m

b) 180 m

c) 175 m

d) None of the above

Question 11: The speed of a boat when travelling downstream is 32 Kms. / Hr. , whereas when travelling upstream it is 28 kms/hr. What is the speed of the boat in still water ?

a) 27 Kms./Hr.

b) 29 Kms./ Hr.

c) 31 Kms./ Hr.

d) Cannot be determined

e) None of these

Question 12: A boat’s speed with the current is 15 kmph and the boat’s speed against the current is 5 kmph. What is the speed of the current?

a) 15 kmph

b) 10 kmph

c) 5 kmph

d) 20 kmph

e) None of the above

Question 13: A train 350 m long takes 36 seconds to cross a man running at a speed of 5 km/h in the direction opposite to that of train. What is the speed of the train?

a) 30 km/h

b) 40 km/h

c) 24 km/h

d) 34 km/h

e) Other than those given as options

Question 14: The speeds of a boat downstream and upstream are 18 km/hr and 8 km/hr respectively. What is the speed of the stream?

a) 2 km/hr

b) 3 km/hr

c) 4 km/hr

d) 5 km/hr

e) None of these

Question 15: Two trains crosses each other in 14 sec when they are moving in opposite direction, and when they are moving in same direction they crosses each other in 3 min 2 sec. Find the speed of the faster train by what percent more than the speed of the slower train ?

a) 16.67%

b) 17.33%

c) 16.33%

d) 17.67%

e) 18.33%

XAT Decision making practice questions

Answers & Solutions:

1) Answer (D)

Let the speed of the plane be p Kmph.
So the speed of plane from A to B will be ‘p+50’ and the speed from B to A will be ‘p-50’.
We notice that the plane goes from B to A stays there for 1 hr and again come back to B with total time duration 12 hrs.
So we have $\frac{3000}{p-50} + 1 + \frac{3000}{p+50} = 12$.
We can clearly see that speed of the plane is 550 which satisfies the above equation.
So from going to A from B the plane takes $\frac{3000}{550-50} = 6$ hrs.
So time at B when plane reaches at A is 2 pm .
Hence the time difference between A and B is 1 hr.

 

Alternatively,
Let speed of flight be s,
Since A is to the east of B, A is ahead of be in time
Let A be ahead of B in time by a hours
Departure from A = 4PM, Arrival at B = 8PM
Travel time = 8 – 4 +a = 4 + a
Since City B is behind city A by ‘a’ hours, the actual travel time is ‘a’ hours more than the difference of local times.
Similarly when one travels from B to A, since B is ahead of A by ‘a’ hrs, actual travel time is ‘a’ hours less than total
i.e. B->A Travel time = (3PM – 8AM) – a = 7 -a
Total distance travelled = Speed $\times$ Time taken ….(1)
From A to B, the wind is favourable / in same direction as flight
Hence from (1), we have
A->B >>> $3000 = (s+50)(4+a) => 3000(7-a) = (s+50)(4+a)(7-a)$ …(2)
B->A >>> $3000 = (s-50)(7-a) => 3000(4+a) = (s-50)(7-a)(4+a)$ …(3)
(2) – (3) => $3000(3-2a) = 100(7-a)(4+a) => a^2-63a+62=0 => a=1/62$
Hence the time difference between A and B is 1 hr.

2) Answer (D)

Let the work done by each technician in one hour be 1 unit.
Therefore, total work to be done = 60 units.
From 11 AM to 5 PM, work done = 6*6 = 36 units.
Work remaining = 60 – 36 = 24 units.
Work done in the next 3 hours = 7 units + 8 units + 9 units = 24 units.
Therefore, the work gets done by 8 PM.

3) Answer (B)

Let the work done by the big pump in one hour be 3 units.
Therefore, work done by each of the small pumps in one hour = 2 units.
Let the total work to be done in filling the tank be 9 units.
Therefore, time taken by the big pump if it operates alone = 9/3 = 3 hours.
If all the pumps operate together, the work done in one hour = 3 + 2*3 = 9 units.
Together, all of them can fill the tank in 1 hour.
Required ratio = 1/3

4) Answer (B)

As machine B’s efficiency is twice as of A’s, Hence, it will complete its work in 30 hours.
And C’s efficiency is putting A and B together i.e. = 20 hours $( (\frac{1}{60} + \frac{1}{30})^{-1})$
Now if all three work together, then it will be completed in x (say) days.

$\frac{1}{x} = \frac{1}{20} + \frac{1}{30} + \frac{1}{60}$

or x = 10 hours

5) Answer (B)

In a normal watch, the minute hand crosses the hour’s hand after every 1 hour 5 minutes and 27 seconds.
So, the third time the hour’s hand crosses the minute’s hand is after 3 hours 16 minutes and 21 seconds.

In this watch, the time taken for this to happen is 3 hours 18 minutes and 15 seconds.
Hence, the watch loses 1 minute and 54 seconds after every 3 hours 18 minutes and 15 seconds.
18 minutes and 15 seconds = 1095 seconds = 1095/3600 $\approx$ .304 hours.
=> 3 hours 18 minutes and 15 seconds = 3.304 hours
So, time lost in a day is $1\frac{54}{60}*\frac{24}{3.304} = \frac{114}{60}*\frac{24}{3.304} \approx 13.8$
So, the time lost by the watch in a day is approximately equal to 13 minutes and 48 seconds.

6) Answer (C)

The relative speed is 15 km/hr = 15 km/60 min = 0.25 km/min = 250 m/min.
Therefore, one minute before they collide, they are at a distance of 250m.

7) Answer (C)

Let the distance between gutter 1 and A be x and between gutter 1 and 2 be y.

Hence, x + y + 2y + x = 20 => 2x+3y=20

Also x = 30kmph * 5/60 = 2.5km

Hence, y = 5km

After the ambulance doubles its speed it goes at 60kmph i.e. 1km per min. Hence, time taken for the rest of the journey = 15*2 + 2.5 = 32.5

It takes 1 min to load and unload the patient.

Hence, total time = 5 + 32.5 + 1 = 38.5 mins

So, the doctor would get 1.5 min to attend to the patient.

XAT Quant formulas PDF

Take XAT Mock Test

8) Answer (B)

Let the length of the tunnel be x and distance of the train to entrance A be y. Let the speeds of train and cat be t and c respectively.

Hence, when the cat runs 3x/8, the train covers y.

=> (3x/8)/c = y/t — (1)

When the cat runs 5x/8 to the other end, the train covers x+y

=>(5x/8)/c = (x+y)/t —(2)

Taking ratio of (1) to (2)

3/5 = y/(x+y) => 3x = 2y —(3)

Substituting (3) in (1)

(2y/8)/c = y/t

=> t = 4c

Hence the ratio t:c is 4:1.

9) Answer (B)

Let the distance between two termini = $P$ km
Let the speed of the bus started from Terminus A be x and that of the bus started from terminus B be y.
The two buses met at a distance of 7km from Terminus A
Since the time of travel for both buses is the same.
$\frac{7}{x}$=$\frac{P-7}{y}$
$\frac{x}{y}$=$\frac{7}{P-7}$     ———– Eq (1)
They met again at a distance of 4 km from terminus B.
Distance travelled by bus which started from Terminus A = P+4
Distance travelled by bus which started from Terminus A = 2P-4
So $\frac{x}{y}$ = $\frac{P+4}{2P-4}$   –Eg (2)
On solving Eq 1& 2, we get P=17 km
Each bus covers a distance of 17*2=34 km on a round trip.
Each bus makes 5 round trips in a day =34*5=170 km
Cost of running one bus = $170 \times 20 = 3400$
$\therefore$ Cost of running both buses = $3400 \times 2 = Rs. 6,800$

10) Answer (B)

When the ball is dropped from 45m height it will cover a distance of 45m while going down after rebound it’ll cover a distance of $45*\frac{3}{5}$ while going up and a distance of $45*\frac{3}{5}$ while going down again. after 2nd rebound it’ll cover a distance of $45*\frac{3}{5}*\frac{3}{5}$ while going up and a distance of $45*\frac{3}{5}*\frac{3}{5}$ while going down again and so on

i.e. total distance traveled by the ball is 45 + $45*\frac{3}{5}$ + $45*\frac{3}{5}$ + $45*\frac{3}{5}*\frac{3}{5}$ + $45*\frac{3}{5}*\frac{3}{5}$ +………..

this form 2 infinite GPs as 45 + $45*\frac{3}{5}$ + $45*\frac{3}{5}*\frac{3}{5}$+……. and $45*\frac{3}{5}$+$45*\frac{3}{5}*\frac{3}{5}$+….

For 1st GP a=45 and r=$\frac{3}{5}$ therefore sum of this infinite GP is $\frac{45}{1-\frac{3}{5}}$ = $\frac{225}{2}$

For 2nd GP a=45*$\frac{3}{5}$  and r=$\frac{3}{5}$ therefore sum of this infinite GP is  $\frac{45*\frac{3}{5}}{1-\frac{3}{5}}$ = $\frac{145}{2}$

Therefore our answer = $\frac{225}{2}+\frac{145}{2}$ = 180 m i.e. option ‘B’

11) Answer (E)

Let the speed of boat in still water be v and the speed of water be x.

Boat speed while going upstream = v-x = 28

Boat speed while going downstream = v+x = 32

=> 2v = 60 => v = 30

Hence, none of these is the correct answer.

12) Answer (C)

With the current => downstream
Against the current => upstream
Let the speed of the boat be ‘s’ and the speed of the river be ‘r’.
So, s – r = 5 and s + r = 15
=>2s = 20 => s = 10 and r = 5 kmph
Speed of the current = 5 kmph

13) Answer (A)

Let the speed of the train be x m/s
Speed of the man = 5km/hr = 1.388m/s
Relative speed of man when he is running in opposite direction = (x+1.388)
However train crossess him in 36 seconds = 350/36 =  9.722 m/s
x+1.388 = 9.722
x = 8.334 m/s
x = 30 km/hr

14) Answer (D)

Let the speed of the boat in still water be ‘u’.
Let the speed of the stream be ‘v’.
The speed of the boat upstream = u-v
The speed of the boat downstream = u+v
It is given that,
u-v = 8 and u+v = 18
Solving them we get, u = 13 and v = 5.
Thus the speed of the stream is 5 km/hr.
Hence the answer to this question is Option D.

15) Answer (A)

let the speed of faster train be F m/s

And slower train be S m/s

When they move in same direction relative speed = (F -S) m/s

Time taken = 14 sec

When they move in opposite direction = (F+S) m/s

Time taken in this case = 182 sec

In both cases they are covering same distance

So , (F+S )× 14 = (F-S ) × 182

12 F = 14 S

F = $\frac{7}{6}$ S

so faster train is 1/6 more than the slower one which means it is 16.67% faster than the slower train.

XAT Solved Previous papers

Take XAT Mock Test

We hope this Time, Speed and Distance  Questions PDF for XAT with Solutions will be helpful to you.