XAT Linear Equation Questions PDF [Important]
Download Linear Equation Questions for XAT PDF – XAT Linear Equation questions PDF by Cracku. Practice XAT solved Linear Equation Questions paper tests, and these are the practice question to have a firm grasp on the Linear Equation topic in the XAT exam. Top 20 very Important Linear Equation Questions for XAT based on asked questions in previous exam papers. The XAT question papers contain actual questions asked with answers and solutions.
Download Linear Equation Questions for XAT
Enroll to XAT 2023 Crash Course
Question 1: A donation box can receive only cheques of ₹100, ₹250, and ₹500. On one good day, the donation box was found to contain exactly 100 cheques amounting to a total sum of ₹15250. Then, the maximum possible number of cheques of ₹500 that the donation box may have contained, is
1) Answer: 12
Solution:
Let the number of 100 cheques, 250 cheques and 500 cheques be x, y and z respectively.
We need to find the maximum value of z.
x + y + z = 100 …… (1)
100x + 250y + 500z = 15250
2x + 5y + 10z = 305 …… (2)
2x + 2y + 2z = 200 ……. (1)
(2) – (1), we get
3y + 8z = 105
At z = 12, x = 3
Therefore, maximum value z can take is 12.
Question 2: If $c=\frac{16x}{y}+\frac{49y}{x}$ for some non-zero real numbers x and y, then c cannot take the value
a) $60$
b) $-50$
c) $-70$
d) $-60$
2) Answer (B)
Solution:
Let $\frac{x}{y}\ be\ t$
Therefore, $c=16t\ +\ \frac{49}{t}$
Applying AM>= GM
$\frac{\left(16t\ +\ \frac{49}{t}\right)}{2}\ge\ \left(16t\times\frac{49}{t}\right)^{\frac{1}{2}}$
$16t\ +\ \frac{49}{t}\ge56$
When t is positive then c is greater than equal to 56.
When t is negative then c is less than equal to -56.
Therefore $c\ \in\ \left(-\infty,\ -56\right]\ ∪\ \left[56,\infty\ \right]$
As -50 is not in the range of c so it is the answer
Question 3: In an examination, there were 75 questions. 3 marks were awarded for each correct answer, 1 mark was deducted for each wrong answer and 1 mark was awarded for each unattempted question. Rayan scored a total of 97 marks in the examination. If the number of unattempted questions was higher than the number of attempted questions, then the maximum number of correct answers that Rayan could have given in the examination is
3) Answer: 24
Solution:
Let the number of questions attempted be x+y out of which x are correct and y are incorrect and the number of questions unattempted be z.
It is given,
x + y + z = 75 …… (1)
3x – y + z = 97 …… (2)
(2)-(1) -> x – y = 11
(1)+(2) -> 2x + z = 86
z > x + y
z > 75 – z
z > 37.5
Minimum possible value of z is 38
2x + 38 = 86
2x = 48
x = 24
The maximum number of correct answers is 24.
Question 4: For natural numbers x, y, and z, if xy + yz = 19 and yz + xz = 51, then the minimum possible value of xyz is
4) Answer: 34
Solution:
It is given, y(x + z) = 19
y cannot be 19.
If y = 19, x + z = 1 which is not possible when both x and z are natural numbers.
Therefore, y = 1 and x + z = 19
It is given, z(x + y) = 51
z can take values 3 and 17
Case 1:
If z = 3, y = 1 and x = 16
xyz = 3*1*16 = 48
Case 2:
If z = 17, y = 1 and x = 2
xyz = 17*1*2 = 34
Minimum value xyz can take is 34.
Question 5: The largest real value of a for which the equation $\mid x + a \mid + \mid x – 1 \mid = 2$ has an infinite number of solutions for x is
a) -1
b) 0
c) 1
d) 2
5) Answer (C)
Solution:
In the question, it is given that the equation $\mid x + a \mid + \mid x – 1 \mid = 2$ has an infinite number of solutions for any value of x. This is possible when x in |x+a| and x in |x-1| cancels out.
Case 1:
x + a < 0, x – 1 $\ge\ $ 0
– a – x + x – 1 = 2
a = -3
Case 2:
x + a $\ge\ $ 0 and x – 1 < 0
x + a – x + 1 = 2
a = 1
Largest value of a is 1.
The answer is option C.
Question 6: Let a and b be natural numbers. If $a^2 + ab + a = 14$ and $b^2 + ab + b = 28$, then $(2a + b)$ equals
a) 8
b) 7
c) 10
d) 9
6) Answer (A)
Solution:
a(a + b + 1) = 14 …… (1)
b(a + b + 1) = 28 …… (2)
$\frac{a}{b}=\frac{1}{2}$
b = 2a
Substituting in (1), we get
a(3a + 1) = 14
$3a^2+a-14=0$
$3a^2-6a+7a-14=0$
$3a\left(a-2\right)+7\left(a-2\right)=0$
Given, a and b are natural numbers.
Therefore, a = 2 and b = 4
2a + b = 2(2) + 4 = 8
The answer is option A.
Question 7: Abdul can go from his home to his favourite basketball ground by taking any of the two roads represented by $y – x = 10$ and $2x + 2y = 15$. The ground is located at a distance of 200 units from each of the roads. What is the possible location of the basketball ground?
a) $(-1.25 + 200\sqrt{2}, 8.75)$
b) $\left(-125 + \frac{200}{\sqrt{2}}, 8.75 + \frac{200}{\sqrt{2}}\right)$
c) $(-1.25 + 100, 8.75 + 100\sqrt{3})$
d) $(-1.25 + 100\sqrt{3}, 8.75 + 100)$
7) Answer (A)
Solution:
Distance of point $\left(-1.25+200\sqrt{2},\ 8.75\right)$ from lines y-x=10 and x+y=15/2
Distance from y-x=10 is $\frac{\left|1.25-200\sqrt{2}+8.75-10\right|}{\sqrt{\ 1}+\sqrt{\ 1}}=200$
Distance from x+y=15/2 is $\frac{\left|-1.25+200\sqrt{2}+8.75-7.5\right|}{\sqrt{\ 1}+\sqrt{\ 1}}=200$
Question 8: If $3x+2\mid y\mid+y=7$ and $x+\mid x \mid+3y=1$ then $x+2y$ is:
a) $-\frac{4}{3}$
b) $\frac{8}{3}$
c) $0$
d) $1$
8) Answer (C)
Solution:
We need to check for all regions:
x >= 0, y >= 0
x >= 0, y < 0
x < 0, y >= 0
x < 0, y < 0
However, once we find out the answer for any one of the regions, we do not need to calculate for other regions since the options suggest that there will be a single answer.
Let us start with x >= 0, y >= 0,
3x + 3y = 7
2x + 3y = 1
Hence, x = 6 and y = -11/3
Since y > = 0, this is not satisfying the set of rules.
Next, let us test x >= 0, y < 0,
3x – y = 7
2x + 3y = 1
Hence, y = -1
x = 2.
This satisfies both the conditions. Hence, this is the correct point.
WE need the value of x + 2y
x + 2y = 2 + 2(-1) = 2 – 2 = 0.
Question 9: A basket of 2 apples, 4 oranges and 6 mangoes costs the same as a basket of 1 apple, 4 oranges and 8 mangoes, or a basket of 8 oranges and 7 mangoes. Then the number of mangoes in a basket of mangoes that has the same cost as the other baskets is
a) 11
b) 13
c) 10
d) 12
9) Answer (B)
Solution:
Let the cost of an apple, an orange and a mango be a, o, and m respectively.
Then it is given that:
2a+4o+6m = a+4o+8m
or a = 2m.
Also, a+4o+8m = 8o + 7m
10m-7m = 4o
3m = 4o.
We can now express the cost of a basket in terms of mangoes only:
2a+4o+6m = 4m+3m+6m = 13m.
Question 10: The price of an apple is twice that of an orange. The price of an orange is thrice that of a banana.If the price of an apple increases by 10%, price of an orange increases by 30% and the price of a banana increases by 20%. Find the percentage increase in the price of 20 apples, 20 oranges and 20 bananas.
a) 19%
b) 17%
c) 15%
d) 13%
10) Answer (B)
Solution:
Let price of banana be x
so price of orange = 3x
and price of apple will be 6x
Price of 20 bananas , apples and oranges = 200 x (1)
Now f the price of an apple increases by 10%,
it becomes = 6.6x
so price of 20 apples = 132x
if price of an orange increases by 30% it becomes = 3.9x
so price of 20 oranges = 78x
if price of a banana increases by 20%
it becomes 1.2 x
so price of 20 bananas = 24x
Now total price of 20 bananas , apples and oranges =234x (2)
So Percentage change in price = $\frac{234x-200x}{200x}\times\ 100=\ 17$%
Question 11: Rahul has just made a $3 \times 3$ magic square, in which, the sum of the cells along any row, column or diagonal, is the same number N. The entries in the cells are given as expressions in x, y, and Z. Find N?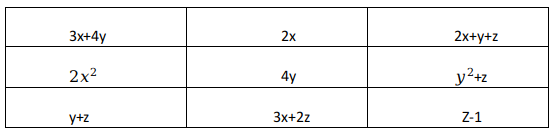
a) 12
b) 36
c) 21
d) 40
e) 24
11) Answer (B)
Solution:
Sum of 3rd row = sum of 2nd column
=> 2x+4y = y+2z-1
=> 2x+3y-2z= -1 ——- (A)
Sum of diagonals are also equal
=> 3x+4y+z-1 = y+z+2x+y+z
=> x+2y-z=1 —–(B)
Solving A and B we get y= 3
Putting it in A, we get x-z = -5 —– (C)
Sum of 1st row = sum of 2nd column
5x+5y+z = 3x+4y+2z
=> 2x +y – z =0
Since y=3, 2x-z = -3 —— (D)
Solving C and D we get x=2 and z=7
Hence N = 36
Question 12: Aron bought some pencils and sharpeners. Spending the same amount of money as Aron, Aditya bought twice as many pencils and 10 less sharpeners. If the cost of one sharpener is ₹ 2 more than the cost of a pencil, then the minimum possible number of pencils bought by Aron and Aditya together is
a) 33
b) 27
c) 30
d) 36
12) Answer (A)
Solution:
Let the number of pencils bought by Aron be “p” and the cost of each pencil be “a”.
Let the number of sharpeners bought Aron be “s” and the cost of each sharpener be “b”.
Now amount spent by Aron will be (pa)+(sb)
Aditya bought (2p) pencils and (s-10) sharpeners. Amount spent will be (2pa)+(s-10)b
Amount spent in both the cases is same
pa + sb = 2pa + (s-10)b or pa=10b
Now its given in the question that cost of sharpener is 2 more than pencil i.e. b=a+2
pa= 10a+20 or a=20/(p-10)
Now the number of pencils has to be minimum, for that we have to find smallest “p” such that both “p” and “a” are integers. The smallest such value is p=11 . Total number of pencils bought will be p+2p=11+22=33
Question 13: If x and y are non-negative integers such that $x + 9 = z$, $y + 1 = z$ and $x + y < z + 5$, then the maximum possible value of $2x + y$ equals
13) Answer: 23
Solution:
We can write x=z-9 and y=z-1 Now we have x+y< z+5
Substituting we get z-9+z-1<z+5 or z<15
Hence the maximum possible value of z is 14
Maximum value of “x” is 5 and maximum value of “y” is 13
Now 2x+y = 10+13=23
Question 14: In May, John bought the same amount of rice and the same amount of wheat as he had bought in April, but spent ₹ 150 more due to price increase of rice and wheat by 20% and 12%, respectively. If John had spent ₹ 450 on rice in April, then how much did he spend on wheat in May?
a) Rs.560
b) Rs.570
c) Rs.590
d) Rs.580
14) Answer (A)
Solution:
Let John buy “m” kg of rice and “p” kg of wheat.
Now let the price of rice be “r” in April. Price in May will be “1.2(r)”
Now let the price of wheat be “w” in April . Price in April will be “1.12(w)”.
Now he spent ₹150 more in May , so 0.2(rm)+0.12(wp)=150
Its also given that he had spent ₹450 on rice in April. So (rm)=450
So 0.2(rm)= (0.2)(450)=90 Substituting we get (wp)=60/0.12 or (wp)=500
Amount spent on wheat in May will be 1.12(500)=₹560
Question 15: Let k be a constant. The equations $kx + y = 3$ and $4x + ky = 4$ have a unique solution if and only if
a) $\mid k\mid\neq2$
b) $\mid k\mid=2$
c) $k\neq2$
d) $k=2$
15) Answer (A)
Solution:
Two linear equations ax+by= c and dx+ ey = f have a unique solution if $\frac{a}{d}\ne\ \frac{b}{e}$
Therefore, $\frac{k}{4}\ne\ \frac{1}{k}$ => $k^2\ne\ 4$
=> k $\ne\ $ |2|
Question 16: Dick is thrice as old as Tom and Harry is twice as old as Dick. If Dick’s age is 1 year less than the average age of all three, then Harry’s age, in years, is
16) Answer: 18
Solution:
Let tom’s age = x
=> Dick=3x
=>harry = 6x
Given,
3x+1 = (x+3x+6x)/3
=> x= 3
Hence, Harry’s age = 18 years
Question 17: Let A, B and C be three positive integers such that the sum of A and the mean of B and C is 5. In addition, the sum of B and the mean of A and C is 7. Then the sum of A and B is
a) 5
b) 4
c) 6
d) 7
17) Answer (C)
Solution:
Given
A+(B+C)/2=5 => 2A+B+C=10….(i)
(A+C)/2 +B=7 => A+2B+C=14…..(ii)
(i)-(ii)=> B-A=4 => B=4+A.
Given, A, B, C are positive integers
If A=1=>B=5 => C=3
If A=2=>B=6 => C=0 but this is invalid as C is positive.
Similarly if A>2 C will be negative and cases are not valid.
Hence, A+B=6.
Question 18: A gentleman decided to treat a few children in the following manner. He gives half of his total stock of toffees and one extra to the first child, and then the half of the remaining stock along with one extra to the second and continues giving away in this fashion. His total stock exhausts after he takes care of 5 children. How many toffees were there in his stock initially?
18) Answer: 62
Solution:
Let the initial number of chocolates be 64x.
First child gets 32x+1 and 32x-1 are left.
2nd child gets 16x+1/2 and 16x-3/2 are left
3rd child gets 8x+1/4 and 8x-7/4 are left
4th child gets 4x+1/8 and 4x-15/8 are left
5th child gets 2x+1/16 and 2x-31/16 are left.
Given, 2x-31/16=0=> 2x=31/16 => x=31/32.
.’. Initially the Gentleman has 64x i.e. 64*31/32 =62 chocolates.
Question 19: A shop sells bags in three sizes: small, medium and large. A large bag costs Rs.1000, a medium bag costs Rs.200, and a small bag costs Rs.50. Three buyers, Ashish, Banti and Chintu, independently buy some numbers of these types of bags. The respective amounts spent by Ashish, Banti and Chintu are equal. Put together, the shop sells 1 large bag, 15 small bags and some medium bags to these three buyers. What is the minimum number of medium bags that the shop sells to them?
a) 5
b) 9
c) 4
d) 10
e) 7
19) Answer (E)
Solution:
Let the amount spent by Ashish is ‘a’, Banti is ‘b’ and Chintu is ‘c’. Given, a = b = c.
One of them has bought a large bag. So, he must have spent at least 1000 rupees. It means, everyone has spent at least a thousand rupees. Or, a +b + c ≥ 3000.
Revenue from small bags = 50*15 = 750.
Revenue from large bag = 1000*1 = 1000. Total revenue excluding from medium bag = 750 + 1000 = 1750.
If 4 medium bags are sold, total revenue = 200*4 + 1750 = 2550, which is less than 3000. Hence, not the right answer.
If 5 medium bags are sold, total revenue = 200*5 + 1750 = 2750, which is less than 3000. Hence, not the right answer.
If 7 medium bags are sold, total revenue = 200*7 + 1750 = 3150, which is more than 3000. Hence, 7 is the correct answer.
Question 20: A person buys 18 local tickets for Rs. 110. Each first class ticket costs Rs. 10 and each second class ticket costs Rs. 3. What will another lot of 18 tickets in which the number of first class and second class tickets are interchanged cost?
a) 112
b) 118
c) 121
d) 124
20) Answer (D)
Solution:
Consider the number of first-class tickets =a and the second-class ticket =b
10a+3b=110
a+b=18
Solving two equations, we get a=8, b=10
After interchanging the number of tickets, the new cost = 10*10+3*8 =124





