XAT Coordinate Geometry Questions PDF [Most Important]
Download Coordinate Geometry Questions for XAT PDF – XAT Coordinate Geometry questions pdf by Cracku. Top 12 very Important Coordinate Geometry Questions for XAT based on asked questions in previous exam papers.
Download Coordinate Geometry Questions for XAT
Enroll to XAT 2023 Crash Course
Question 1: In the xy coordinate system, if (a, b) and (a + 3, b + k) are two points on the line defined
by the equation x = 3y – 7, then k = ?
a) 7/3
b) 1
c) 9
d) 3
1) Answer (B)
Solution:
In the xy coordinate system, if (a, b) and (a + 3, b + k) are two points on the line defined by the equation x = 3y – 7, then they must satisfy the equation .
so , we get a = 3b – 7
and a+3 = 3(b+k) – 7
On solving these equations , we get k = 1
Question 2: Area of the triangle formed by the graph of the line 2x – 3y + 6 = 0 along with the coordinate axes is
a) 1/2 sq. units
b) 3/2 sq. units
c) 3 sq. units
d) 6 sq. units
2) Answer (C)
Solution:
the line 2x – 3y + 6 = 0 meets the coordinate axes at (-3,0) and (0,2).
So, base=2 and height = 3
Area of the triangle = $\frac{bh}{2}$
= 3
Question 3: ABCD is a rectangle in the clockwise direction. The coordinates of A are (1,3) and the coordinates of C are (5,1), the coordinates of vertices B and D satisfy the line $y=2x+c$, then what will be the coordinates of the mid-point of BC.
a) $(\frac{5}{2},\frac{7}{2})$
b) $(\frac{9}{2},\frac{5}{2})$
c) $(\frac{9}{5},\frac{7}{2})$
d) $(3,2)$
3) Answer (B)
Solution:

Midpoint of AC passes through the line y = 2x + c
Midpoint of AC = (3,2)
2 = 6 + c
c = -4
Line passing through B is y = 2x – 4
(slope of AB)(slope of BC) = -1
$\left(\ \frac{\ y-1}{x-5}\right)\left(\ \frac{\ y-3}{x-1}\right)=-1$
Substituting y = 2x – 4 and solving, we get
B(2,0) or B(4,4)
B cannot lie on X-axis. Therefore, co-ordinates of B = (4,4)
Midpoint of BC = $\left(\frac{9}{2},\frac{5}{2}\right)$
The answer is option B.
Question 4: There are 12 points in a two-dimensional plane with following coordinates: Points A, B, C, D, E,F, G have coordinates (1, 0), (2, 0), (3, 0), (4, 0), (5, 0), (6, 0) and (7, 0) respectively. Points H, I, J havecoordinates (1, 1), (2, 2) and (3, 3) respectively. Points K, L have coordinates (4, -2) and (5, -3)respectively. The number of circles possible with these points are?
a) 179
b) 158
c) 168
d) 147
4) Answer (A)
Solution:
A, B, C, D, E, F, G all lie of a single line
H, I, J all lie on another single line
K, L lie on another single line
If we are given three points which are not collinear than we can draw a circle from these three points
Question 5: Let T be the triangle formed by the straight line 3x + 5y – 45 = 0 and the coordinate axes. Let the circumcircle of T have radius of length L, measured in the same unit as the coordinate axes. Then, the integer closest to L is
5) Answer: 9
Solution:
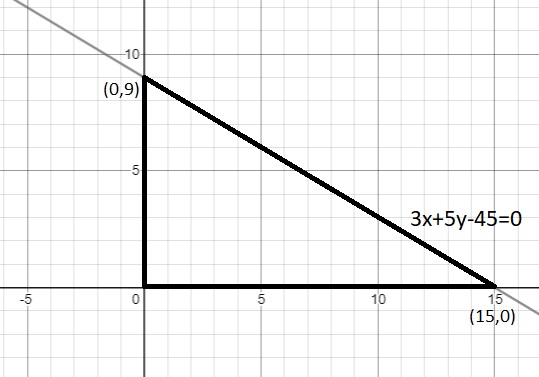
In any right triangle, the circumradius is half of the hypotenuse. Here,L=$\ \frac{\ 1}{2}\ $* the length of the hypotenuse = $\ \frac{\ 1}{2}$($\sqrt{\ 15^2+9^2}$) = $\ \frac{\ 1}{2}\ $*$\sqrt{\ 306}$ = $\ \frac{\ 1}{\ 2}\times\ $17.49 = 8.74
Hence, the integer close to L = 9
Question 6: The diameter of the circumcircle of the triangle formed by the line $24x + 7y =168$ and the coordinate axes is
a) $15\sqrt{2}$
b) $24$
c) $25$
d) $12\sqrt{3}$
6) Answer (C)
Solution:
Let’s rewrite the equation $24x + 7y =168$ in intercept form
$\frac{x}{7}+\frac{y}{24}$ = 1
$\therefore$ The co-ordinates of the triangle are (7,0),(0,0),(0,24)
Diameter of the circumcircle formed by the vertices is given by the hypotenuse, which is between (7,0) and (0,24).
Distance between the co-ordinates (7,0) and (0,24) =$\sqrt{7^{2} +24^{2}}$ =25.
Hence C is the correct answer.
Question 7: The coordinates of a triangle ABC are A(1, 5), B(-2, 3), and C(0,-4); find the equation of the median AD? ·
a) 7x-3y+-8= 0
b) 5x-4y+15=O
c) x+3y-16=0
d) 11x-4y+9=0
7) Answer (D)
Solution:
Given that $\triangle$ABC
Since AD is the median to BC, D will be mid point of BC. So coordinates of D = ($\frac{-2+0}{2} ,\frac{3-4}{2}$) = (-1 ,$\frac{-1}{2}$)
Equation of line passing through points A(1,5) and D(-1,$\frac{-1}{2}$) will be :
$(y-x_{1})=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}(x-x_{1})$ (Here $(x_{1},y_{1})=(1,5)$ , $(x_{2},y_{2})=(-1,\frac{-1}{2})$)
$(y-5)=\frac{(\frac{-1}{2})-(5)}{(-1)-(1)}(x-1)$
$4(y-5)=11(x-1)$
$11x-4y+9=0$
Question 8: ln a plane rectangular coordinate system, points L, M, N and O are represented by the coordinates (-5, 0), (1,-1), (0, 5), and (-1, 5) respectively. Consider a variable point P in the same plane. The minimum value of PL + PM + PN + PO is
a) $1+\sqrt{37}$
b) $5\sqrt{2}+2\sqrt{10}$
c) $\sqrt{41}+\sqrt{37}$
d) $\sqrt{41}+1$
e) None of these
8) Answer (B)
Solution:
$(PL + PN)$ will be minimum if P lies on LN, and $(PM + PO)$ will be minimum if P lies on OM.
=> P must be the intersection point of the diagonals of the quadrilateral.
$\therefore$ Min (PL + PM + PN + PO)
= $LN + OM$
= $(\sqrt{(0 + 5)^2 + (5 – 0)^2}) + (\sqrt{(1 + 1)^2 + (-1 – 5)^2})$
= $(\sqrt{25 + 25}) + (\sqrt{4 + 36})$
= $\sqrt{50} + \sqrt{40} = 5 \sqrt{2} + 2 \sqrt{10}$
Question 9: Two diagonals of a parallelogram intersect each other at coordinates (17.5, 23.5). Two adjacent points of the parallelogram are (5.5, 7.5) and (13.5, 16). Find the lengths of the diagonals.
a) 15 and 30
b) 15 and 40
c) 17 and 30
d) 17 and 40
e) Multiple solutions are possible
9) Answer (D)
Solution:

Using distance formula,
$CX = \sqrt{(17.5 – 5.5)^2 + (23.5 – 7.5)^2} = \sqrt{12^2 + 16^2}$
= $\sqrt{144 + 256} = \sqrt{400} = 20$
=> $AC = 2 \times CX = 40$
$BX = \sqrt{(17.5 – 13.5)^2 + (23.5 – 16)^2} = \sqrt{4^2 + 7.5^2}$
= $\sqrt{16 + 56.25} = \sqrt{72.25} = 8.5$
=> $BD = 2 \times BX = 17$
Question 10: Consider a triangle drawn on the X-Y plane with its three vertices at (41, 0), (0, 41) and (0, 0), each vertex being represented by its (X,Y) coordinates. The number of points with integer coordinates inside the triangle (excluding all the points on the boundary) is
a) 780
b) 800
c) 820
d) 741
10) Answer (A)
Solution:
The number of points on x = 1 is 39. The number of points on x = 2 is 38 and so on till x = 39, which has one point.
So, the total is 1+2+3+…+39 = $\frac{39*40}{2}$ = 780.
Question 11: What are the coordinates of the mid point of the segment joining points C(5,2) and D(-1,-8).
a) (2, 3)
b) (2, -3)
c) (-2 ,-3)
d) (-2, 3)
11) Answer (B)
Solution:
Coordinates of the mid point of the segment joining points $(x_1,y_1)$ and $(x_2,y_2)$ = $(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})$
Thus, coordinates of the mid point of the segment joining points C(5,2) and D(-1,-8)
= $(\frac{5-1}{2},\frac{2-8}{2})$
= $(\frac{4}{2},\frac{-6}{2})$
= $(2,-3)$
=> Ans – (B)
Question 12: Point P is the midpoint of seg AB. Coordinates of P are (1,1) and A are (4,3). What are the coordinates of point B?
a) (2, 1)
b) (-2, -1)
c) (2, -1)
d) (-2, 1)
12) Answer (B)
Solution:
Coordinates of mid point of line joining A $(x_1,y_1)$ and B $(x_2,y_2)$ = $(\frac{x_1 + x_2}{2} , \frac{y_1 + y_2}{2})$
Let coordinates of B $(x , y)$
A = (4,3) and P = (1,1)
=> $1 = \frac{4 + x}{2}$
=> $x = 2 – 4 = -2$
Similarly, $1 = \frac{3 + y}{2}$
=> $y = 2 – 3 = -1$
Thus, coordinates of B (-2,-1)







