Time and Work Questions for MAH – CET PDF

Here you can download the important MAH – CET Time and Work Questions PDF by Cracku. Very Important MAH – CET 2022 and These questions will help your MAH – CET preparation. So kindly download the PDF for reference and do more practice.

Download Time and Work Questions for MAH – CET PDF

Enroll to MAH-CET Crash Course

Question 1: If A and B can do a piece of work in 20 days,and A alone can do the same work in 30 days, then in how many days can B alone complete the same work?

a) 60

b) 40

c) 75

d) 50

1) Answer (A)

Solution:

Given,

A and B together can do the work in 20 days.

A alone can do the work in 30 days

Let the total work be 60 ( LCM of 20 & 30)

Efficiency = $\frac{\ Total\ work}{time\ taken}\ $

Efficiency of (A + B) = $\frac{60}{20}=\ 3$

Efficiency of A alone = $\frac{60}{30}=2$

so, Efficiency of B = Efficiency of (A+B) – Efficiency of A

i.e; 3 – 2 = 1

Time in which B alone can complete the work = $\frac{60}{1}=60\ days$

Hence, option A is correct.

Question 2: A, B and C can do a piece of work in 10, 15 and 30 days, respectively. If B and C both assist A on every third day,then in how many days can the work be completed?

a) $8\frac{1}{2}$

b) 5

c) 8

d) $7\frac{1}{2}$

2) Answer (C)

Solution:

Let the total work done by A,B and C is 30 units. (LCM of 10,15 and 30)

Efficiency = one day work

$efficiency\ =\ \frac{total\ work}{time\ taken}$

Efficiency of A,B and C is 3,2 and 1 unit respectively

Work done by A in first two days = $3\times\ 2=6$

Work done on 3rd day = (3 + 2 + 1) = 6

total work done in 3 days = 6 + 6 = 12

work done in next 3 days = 12

Total work till end of the 6th day = 12 + 12 = 24

Remaining work = 30 – 24 = 6

so, A alone will do 6 unit work in next two days ( as B and C assist A on every 3rd day)

So total work finish in 6 + 2 = 8 days.

Question 3: Anil can paint a house in 12 days while Barun can paint it in 16 days. Anil, Barun, and Chandu undertake to paint the house for ₹ 24000 and the three of them together complete the painting in 6 days. If Chandu is paid in proportion to the work done by him, then the amount in INR received by him is

Question 4: Mira and Amal walk along a circular track, starting from the same point at the same time. If they walk in the same direction, then in 45 minutes, Amal completes exactly 3 more rounds than Mira. If they walk in opposite directions, then they meet for the first time exactly after 3 minutes. The number of rounds Mira walks in one hour is

Question 5: One day, Rahul started a work at 9 AM and Gautam joined him two hours later. They then worked together and completed the work at 5 PM the same day. If both had started at 9 AM and worked together, the work would have been completed 30 minutes earlier. Working alone, the time Rahul would have taken, in hours, to complete the work is

a) 11.5

b) 10

c) 12.5

d) 12

5) Answer (B)

View Video Solution

Solution:

Let Rahul work at a units/hr and Gautam at b units/hour
Now as per the condition :
8a+6b =7.5a+7.5b
so we get 0.5a=1.5b
or a=3b
Therefore total work = 8a +6b = 8a +2a =10a
Now Rahul alone takes 10a/10 = 10 hours.

Take Free MAH-CET mock tests here

Question 6: Two pipes A and B are attached to an empty water tank. Pipe A fills the tank while pipe B drains it. If pipe A is opened at 2 pm and pipe B is opened at 3 pm, then the tank becomes full at 10 pm. Instead, if pipe A is opened at 2 pm and pipe B is opened at 4 pm, then the tank becomes full at 6 pm. If pipe B is not opened at all, then the time, in minutes, taken to fill the tank is

a) 144

b) 140

c) 264

d) 120

6) Answer (A)

View Video Solution

Solution:

Let A fill the tank at x liters/hour and B drain it at y liters/hour
Now as per Condition 1 :
We get Volume filled till 10pm = 8x-7y       (1) .
Here A operates for 8 hours and B operates for 7 hours .
As per condition 2
We get Volume filled till 6pm = 4x-2y        (2)
Here A operates for 4 hours and B operates for 2 hours .
Now equating (1) and (2)
we get 8x-7y =4x-2y
so we get 4x =5y
y =4x/5
So volume of tank = $8x-7\times\ \frac{4x}{5}=\frac{12x}{5}$
So time taken by A alone to fill the tank = $\frac{\frac{12x}{5}}{x}=\frac{12}{5}hrs\ $
= 144 minutes

Question 7: Anil can paint a house in 60 days while Bimal can paint it in 84 days. Anil starts painting and after 10 days, Bimal and Charu join him. Together, they complete the painting in 14 more days. If they are paid a total of ₹ 21000 for the job, then the share of Charu, in INR, proportionate to the work done by him, is

a) 9000

b) 9200

c) 9100

d) 9150

7) Answer (C)

View Video Solution

Solution:

Let Entire work be W
Now Anil worked for 24 days
Bimal worked for 14 days and Charu worked for 14 days .
Now Anil Completes W in 60 days
so in 24 days he completed 0.4W
Bimal completes W in 84 Days
So in 14 Days Bimal completes = $\frac{W}{6}$
Therefore work done by charu = $W-\frac{W}{6}-\frac{4W}{10}$= $\frac{26W}{10}$=$\frac{13W}{30}$
Therefore proportion of Charu = $\frac{13}{30}\times\ 21000$=9100

Question 8: Two trains A and B were moving in opposite directions, their speeds being in the ratio 5 : 3. The front end of A crossed the rear end of B 46 seconds after the front ends of the trains had crossed each other. It took another 69 seconds for the rear ends of the trains to cross each other. The ratio of length of train A to that of train B is

a) 3:2

b) 5:3

c) 2:3

d) 2:1

8) Answer (A)

View Video Solution

Solution:

Considering the length of train A = La, length of train B = Lb.

The speed of train A be 5*x, speed of train B be 3*x.

From the information provided :

The front end of A crossed the rear end of B 46 seconds after the front ends of the trains had crossed each other.

In this case, train A traveled a distance equivalent to the length of train B which is Lb at a speed of 5*x+3*x = 8*x because both the trains are traveling in the opposite direction.

Hence (8*x)*(46) = Lb.

In the information provided :

It took another 69 seconds for the rear ends of the trains to cross each other.

In the next 69 seconds

The train B traveled a distance equivalent to the length of train A in this 69 seconds.

Hence (8*x)*(69) = La.

La/Lb = 69/46 = 3/2 = 3 : 2

Question 9: Amar, Akbar and Anthony are working on a project. Working together Amar and Akbar can complete the project in 1 year, Akbar and Anthony can complete in 16 months, Anthony and Amar can complete in 2 years. If the person who is neither the fastest nor the slowest works alone, the time in months he will take to complete the project is

Question 10: Anu, Vinu and Manu can complete a work alone in 15 days, 12 days and 20 days, respectively. Vinu works everyday. Anu works only on alternate days starting from the first day while Manu works only on alternate days starting from the second day. Then, the number of days needed to complete the work is

a) 5

b) 8

c) 6

d) 7

10) Answer (D)

View Video Solution

Solution:

Let the total amount of work be 60 units.

Then Anu, Vinu, and Manu do 4, 5, and 3 units of work per day respectively.

On the 1st day, Anu and Vinu work. Work done on the 1st day = 9 units

On the 2nd day, Manu and Vinu work. Work done on the 2nd day = 8 units

This cycle goes on. And in 6 days, the work completed is 9+8+9+8+9+8 = 51 units.

On the 7th day, again Anu and Vinu work and complete the remaining 9 units of work. Thus, the number of days taken is 7 days.

Question 11: Two trains cross each other in 14 seconds when running in opposite directions along parallel tracks. The faster train is 160 m long and crosses a lamp post in 12 seconds. If the speed of the other train is 6 km/hr less than the faster one, its length, in m, is

a) 184

b) 192

c) 190

d) 180

11) Answer (C)

View Video Solution

Solution:

Speed of the faster train = $\frac{160}{12}=\frac{40}{3}\ $ m/s

Speed of the slower train = $\frac{40}{3}-\left(6\times\ \frac{5}{18}\right)=\frac{35}{3}$ m/s

Sum of speeds (when the trains travel towards each other) = $\frac{40}{3}+\frac{35}{3}=25$ m/s

Let the slower train be $x$ metres long; then: $\frac{160+x}{25}=14$

On solving, $x=190\ m$

Question 12: In a 1000 metre race, Rahul reaches the finishing line 5 seconds before than Raj and beats Raj by 50 metre. What is Rahul’s speed (in m/s)?

a) $11\frac{9}{19}$

b) $9\frac{9}{19}$

c) $10\frac{10}{19}$

d) $9\frac{10}{19}$

12) Answer (C)

Solution:

Let speed of Raj be v1 and speed of Rahul be v2
Now Rahul reaches 5 seconds before Raj and beats him by 50m
so Raj covers 50m in 5 seconds
so v1 = 10m/s
Now When Raj covers 950m Rahul covers 1000m (in the same time )
so we get $\frac{v1}{v2}=\frac{1000}{950}$
v1 =$\frac{200}{19}\ =10\ \frac{10}{19}\ $ m/sec

Question 13: Given: Anuj takes 1 day to complete a job. Bharat takes twice the time as Anuj to complete the same job. Chetan takes twice the time as Bharat to complete that job. Dhiraj takes twice the time as Chetan to complete that job.
(A) Chetan and Dhiraj will take 8/3 days to complete the work
(B) The second fastest pair to complete the work is Anuj and Dhiraj
(C) The second slowest pair to complete the work is Bharat and Dhiraj
(D) Bharat and Dhiraj will take 4/3 days to complete the work

a) (A), (B) and (C) only

b) (A) and (D) only

c) (A) and (C) only

d) (A) only

13) Answer (C)

Solution:

Anuj takes 1 day to complete
Bharat takes 2 days
Chetan takes 4 days and Dhiraj takes 8 days to complete
option A chetan and Dhiraj together will take $\frac{4\times\ 8}{4+8}=\frac{32}{12}=\frac{8}{3\ }days$so A is correct.
Now calculating for all we get AB in 2/3 days AC in 4/5 days AD in 8/9 days BC in 8/6 days BD in 16/10 days
So we can say BD is 2nd slowest pair
Hence A and C are correct

Question 14: Four friends, Ashish, Brian, Chaitra, and Dorothy, decide to jog for 30 minutes inside a stadium with a circular running track that is 200 metres long. The friends run at different speeds. Ashish completes a lap exactly every 60 seconds. Likewise, Brian, Chaitra and Dorothy complete a lap exactly every 1 minute 30 seconds, 40 seconds and 1 minute 20 seconds respectively. The friends begin together at the start line exactly at 4 p.m. What is the total of the numbers of laps the friends would have completed when they next cross the start line together ?

a) 43

b) 36

c) They will never be at the start line together again before 4:30 p.m.

d) 47

e) 28

14) Answer (D)

Solution:

All the four friends will meet at the starting point after LCM(60,90,40,80) = 720 seconds.

Number of laps by A in 720 seconds = 12

Number of laps by B in 720 seconds = 8

Number of laps by C in 720 seconds = 18

Number of laps by D in 720 seconds = 9

Together they complete = 47 laps

Question 15: On the bank of the pristine Tunga river, a deer and a tiger are joyfully playing with each other. The deer notices that it is 40 steps away from the tiger and starts running towards it. At the same time, the tiger starts running away from the deer. Both run on the same straight line. For every five steps the deer takes, the tiger takes six. However, the deer takes only two steps to cover the distance that the tiger covers in three. In how many steps can the deer catch the tiger?

a) 200

b) To solve this, the length of a deer’s step must also be given.

c) 120

d) 360

e) 320

15) Answer (A)

Solution:

Let speed of deer = 5steps/second and speed of tiger = 6 steps/sec

Let deer cover 1 m in a step => tiger covers 2/3 m in a step

Hence speed of deer = 5m/s and spped of tiger = 6 x 2/3 m/s = 4m/s

Hence time taken by a deer to catch tiger = 40 seconds

Distance travelled by deer in 40 seconds = 5 x 40 =200 steps

Question 16: Swati can row a boat on still water at a speed of 5 km/hr. However, on a given river, it takes her 1 hour more to row the boat 12 km upstream than downstream. One day, Swati rows the boat on this river from X to Y, which is N km upstream from X. Then she rows back to X immediately. If she takes at least 2 hours to complete this round trip, what is the minimum possible value of N?

a) 3

b) 4.8

c) 2

d) 3.6

e) 2.1

Get 5 MAH-CET mocks at just Rs.299

16) Answer (B)

Solution:

Let the speed of the stream be x

$\frac{12}{5-x}=\frac{12}{5+x}+1$

The value of x satisfying the above equation is 1

Now,

$\frac{N}{5+1}+\frac{N}{5-1}\ge2$

$\frac{2N+3N}{12}\ge2$

=> $N\ge4.8$

Question 17: At any point of time, let x be the smaller of the two angles made by the hour hand with the minute hand on an analogue clock (in degrees). During the time interval from 2:30 p.m. to 3:00 p.m., what is the minimum possible value of x?

a) 45

b) 105

c) 90

d) 0

e) 75

17) Answer (C)

Solution:

The difference between the hour and minute hand of a clock is given by $\left|30H-5.5m\right|$. Here H is the current hour and m represents the number of completed minutes in the current hour.

In the given time frame of 2: 30 to 3: 00 pm.

At 2 : 30 pm the angle = $\left|30\cdot2-5.5\cdot30\right|\ =\ 105\ \deg rees$

At 3: 00 pm the angle = $\left|30\cdot3-5.5\cdot0\right|\ =\ 90\ \deg rees$

The function of $\left|30\cdot H-5.5\cdot m\right|\ =\ $ constantly increases as the value of m increases from 31, 32……………. 59.

Because of the modulus function, the net value of the function remains positive

Between 2: 30 to 2: 59 the angle is constantly increasing. The minimum value is 2: 30 which is equal to 105 degrees which is greater than the 90 degrees when the time is 3: 00.

Hence 90 degrees is the minimum angle.

Question 18: Two circular tracks T1 and T2 of radii 100 m and 20 m, respectively touch at a point A. Starting from A at the same time, Ram and Rahim are walking on track T1 and track T2 at speeds 15 km/hr and 5 km/hr respectively. The number of full rounds that Ram will make before he meets Rahim again for the first time is

a) 5

b) 3

c) 2

d) 4

18) Answer (B)

View Video Solution

Solution:

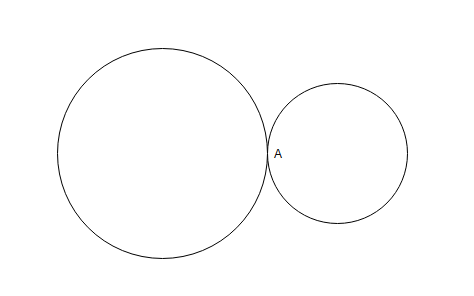
To complete one round Ram takes 100m/15kmph and Rahim takes 20m/5kmph

They meet for the first time after L.C.M of (100m/15kmph , 20m/5kmph) = 100m/5kmph=20m/kmph.

Distance traveled by Ram =20m/kmph * 15kmph =300m.

So, he must have ran 300/100=3 rounds.

Note:

CAT gave both 2 and 3 as correct answers because of the word ‘before‘.

Question 19: A and B are two points on a straight line. Ram runs from A to B while Rahim runs from B to A. After crossing each other. Ram and Rahim reach their destination in one minute and four minutes, respectively. if they start at the same time, then the ratio of Ram’s speed to Rahim’s speed is

a) $\frac{1}{2}$

b) $\sqrt{2}$

c) $2$

d) $2\sqrt{2}$

19) Answer (C)

View Video Solution

Solution:

Let the speed of Ram be v(r) and the speed of Rahim be v(h) respectively. Let them meet after time “t” from the beginning.

Hence Ram will cover v(r)(t) during that time and Rahim will cover v(h)t respectively.

Now after meeting Ram reaches his destination in 1 min i.e. Ram covered v(h)t in 1 minute or v(r)(1)= v(h)(t)

Similarly Rahim reaches his destination in 4 min i.e. Rahim covered v(r)t in 4 minutes or v(h)(4)= v(r)(t)

Dividing both the equations we get $\frac{v\left(r\right)}{4v\left(h\right)}=\frac{v\left(h\right)}{v\left(r\right)}\ or\ \frac{v\left(r\right)}{v\left(h\right)}=2$ Hence the ratio is 2.

Question 20: In a car race, car A beats car B by 45 km. car B beats car C by 50 km. and car A beats car C by 90 km. The distance (in km) over which the race has been conducted is

a) 475

b) 450

c) 500

d) 550

20) Answer (B)

View Video Solution

Solution:

Now car A beats car B by 45km. Let the speed of car A be v(a) and speed of car B be v(b).

$\frac{v\left(a\right)}{v\left(b\right)}=\frac{m}{m-45}$ …..(1)where ‘”m” is the entire distance of the race track.

Moreover $\frac{v\left(b\right)}{v\left(c\right)}=\frac{m}{m-50}$…….(2)

and finally $\frac{v\left(a\right)}{v\left(c\right)}=\frac{m}{m-90}$……(3)

Multiplying (1) and (2) we get (3). $\frac{m}{m-90}=\frac{m}{m-45}\left(\frac{m}{m-50}\right)$

Solving we get m=450 which is the length of the entire race track

Question 21: John takes twice as much time as Jack to finish a job. Jack and Jim together take one-thirds of the time to finish the job than John takes working alone. Moreover, in order to finish the job, John takes three days more than that taken by three of them working together. In how many days will Jim finish the job working alone?

Question 22: The distance from B to C is thrice that from A to B. Two trains travel from A to C via B. The speed of train 2 is double that of train 1 while traveling from A to B and their speeds are interchanged while traveling from B to C. The ratio of the time taken by train 1 to that taken by train 2 in travelling from A to C is

a) 5:7

b) 4:1

c) 1:4

d) 7:5

22) Answer (A)

View Video Solution

Solution:

Let the distance from A to B be “x”, then the distance from B to C will be 3x. Now the speed of Train 2 is double of Train 1. Let the speed of Train 1 be “v”, then the speed of Train 2 will be “2v” while travelling from A to B.

Time taken by Train 1 = (x/v)

Time taken by Train 2 = (x/2v)

Now from B to C distance is “3x” and the speed of Train 2 is (v) and the speed of Train 1 is (2v).

Time taken by Train 1 = 3x/2v

Time taken by Train 2 = 3x/v

Total time taken by Train 1 = x/v(1+(3/2)) = (5/2)(x/v)

Total time taken by Train 2 = x/v(3+(1/2))= (7/2)(x/v)

Ratio of time taken = $\frac{5}{\frac{2}{\frac{7}{2}}}=\frac{5}{7}$

Question 23: Anil, Sunil, and Ravi run along a circular path of length 3 km, starting from the same point at the same time, and going in the clockwise direction. If they run at speeds of 15 km/hr, 10 km/hr, and 8 km/hr, respectively, how much distance in km will Ravi have run when Anil and Sunil meet again for the first time at the starting point?

a) 4.8

b) 4.6

c) 5.2

d) 4.2

23) Answer (A)

View Video Solution

Solution:

Anil and Sunil will meet at a first point after LCM ( $\frac{3}{15},\frac{3}{10}$) = 3/5 hr

In the mean time, distance travelled by ravi = 8 * 3/5 = 4.8 km

Question 24: A and B are two railway stations 90 km apart. A train leaves A at 9:00 am, heading towards B at a speed of 40 km/hr. Another train leaves B at 10:30 am, heading towards A at a speed of 20 km/hr. The trains meet each other at

a) 11 : 45 am

b) 11 : 20 am

c) 11 : 00 am

d) 10 : 45 am

24) Answer (C)

View Video Solution

Solution:

The distance travelled by A between 9:00 Am and 10:30 Am is 3/2*40 =60 km.

Now they are separated by 30 km

Let the time taken to meet =t

Distance travelled by A in time t + Distance travelled by B in time t = 30

40t + 20t =30 => t=1/2 hour

Hence they meet at 11:00 AM

Question 25: Vimla starts for office every day at 9 am and reaches exactly on time if she drives at her usual speed of 40 km/hr. She is late by 6 minutes if she drives at 35 km/hr. One day, she covers two-thirds of her distance to office in one-thirds of her usual total time to reach office, and then stops for 8 minutes. The speed, in km/hr, at which she should drive the remaining distance to reach office exactly on time is

a) 29

b) 26

c) 28

d) 27

25) Answer (C)

View Video Solution

Solution:

Let distance = d

Given, $\frac{d}{35}-\frac{d}{40}=\frac{6}{60}$

=> d = 28km

The actual time  taken to travel 28km = 28/40 = 7/10 hours = 42 min.

Given time taken to travel 58/3 km = 1/3 *42 = 14 min.

Then a break of 8 min.

To reach on time, he should cover remaining 28/3 km in 20 min => Speed = $\frac{\left(\frac{28}{3}\right)}{\frac{20}{60}}=28\ $ km/hr

Take MAH-CET Mock Tests

Enroll to CAT 2022 course