CAT Geometry Questions form an important part of CAT Geometry. You can expect close to 4-5 questions in the 22-question format of the paper. Geometry is one of the most feared topics among the candidates. In this article, we will look into the CAT Geometry Questions (with Notes) PDF, which includes All the important CAT Geometry Formulae and important CAT Geometry Questions with Solutions. These are a good source for practice; If you want to practice these questions, you can download the PDF below, which is completely Free.
Download CAT 2022 Geometry Questions
Enroll for CAT 2022 Online Course
- CAT Geometry – Tip 1: Questions based on Geometry appear in the CAT test almost every year. Understand the CAT Geometry Syllabus; It is one of the most important topics and hence should not be avoided. Based on our analysis of the CAT 2021 Paper this was the CAT Geometry Weightage: 3-4 questions were asked from Geometry.
- CAT Geometry – Tip 2: The subject covers wide-ranging topics, from concepts such as Circles, Triangles, Solids, etc. Getting yourself acquainted with the basics of these concepts will help you solve the problems. Learn all the major properties of Triangles, Circles, Quadrilaterals, and also the Mensuration concepts. You can learn all the Important CAT Geometry Formulas here.
- CAT Geometry – Tip 3: For CAT, Geometry is considered slightly challenging in all the quant topics. A strong foundation in this topic will aid a student in answering the Geometry questions. Every year around one-third of the questions are asked from Geometry in the CAT Exam.
Question 1: A solid right circular cone of height 27 cm is cut into two pieces along a plane parallel to its base at a height of 18 cm from the base. If the difference in volume of the two pieces is 225 cc, the volume, in cc, of the original cone is
a) 243
b) 232
c) 256
d) 264
1) Answer (A)
Solution:
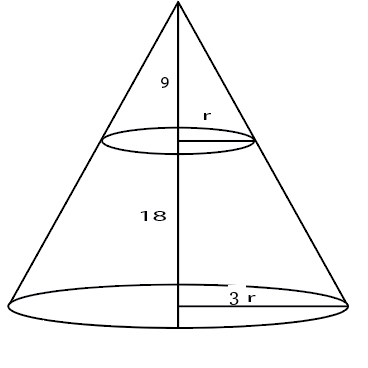
Let the base radius be 3r.
Height of upper cone is 9 so, by symmetry radius of upper cone will be r.
Volume of frustum=$\frac{\pi}{3}\left(9r^2\cdot27-r^2.9\right)$
Volume of upper cone = $\frac{\pi}{3}.r^2.9$
Difference= $\frac{\pi}{3}\cdot9\cdot r^2\cdot25=225$ => $\frac{\pi}{3}\cdot r^2=1$
Volume of larger cone = $\frac{\pi}{3}\cdot9r^2\cdot27=243$
Question 2: A circle is inscribed in a rhombus with diagonals 12 cm and 16 cm. The ratio of the area of circle to the area of rhombus is
a) $\frac{6\pi}{25}$
b) $\frac{5\pi}{18}$
c) $\frac{3\pi}{25}$
d) $\frac{2\pi}{15}$
2) Answer (A)
Solution:
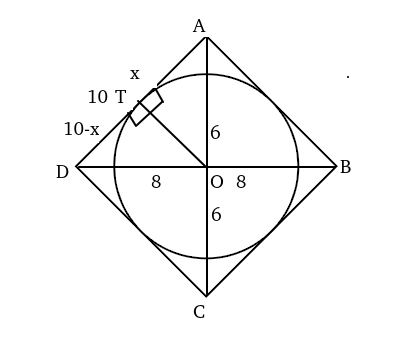
Let the length of radius be ‘r’.
From the above diagram,
$x^2+r^2=6^2\ $….(i)
$\left(10-x\right)^2+r^2=8^2\ $—-(ii)
Subtracting (i) from (ii), we get:
x=3.6 => $r^2=36-\left(3.6\right)^2$ ==> $r^2=36-\left(3.6\right)^2\ =23.04$.
Area of circle = $\pi\ r^2=23.04\pi\ $
Area of rhombus= 1/2*d1*d2=1/2*12*16=96.
.’. Ratio of areas = 23.04$\pi\ $/96=$\frac{6\pi}{25}$
Question 3: Let C be a circle of radius 5 meters having center at O. Let PQ be a chord of C that passes through points A and B where A is located 4 meters north of O and B is located 3 meters east of O. Then, the length of PQ, in meters, is nearest to
a) 8.8
b) 7.8
c) 6.6
d) 7.2
3) Answer (A)
Solution:
We can form the following figure based on the given information:
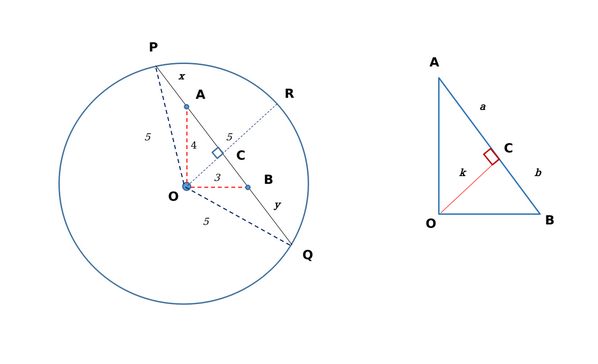
Since OA = 4 m and OB=3 m; AB = 5 m. OR bisects the chord into PC and QC.
Since AB = 5 m, we have $a+b = 5 …(i)$ Also, $4^2\ -k^2=a^2…\left(ii\right)$ and $3^2\ -k^2=b^2…\left(iii\right)$
Subtracting (iii) from (ii), we get: $a^2\ -b^2=7…\left(iv\right)$
Substituting (i) in (iv), we get $a – b = 1.4 …(v)$; $\left[\left(a+b\right)\left(a\ -b\right)=7;\ \therefore\ \left(a-b\right)=\frac{7}{5}\right]$
Solving (i) and (v), we obtain the value of $a=3.2$ and $b=1.8$
Hence, $k^2\ =\ 5.76$
Moving on to the larger triangle $\triangle\ POC$, we have $5^2-k^2=\left(x+a\right)^2$;
Substituting the previous values, we get: $(25-5.76)=\left(x+3.2\right)^2$
$\sqrt{19.24}=\left(x+3.2\right)$ or $x = 1.19 m$
Similarly, solving for y using $\triangle\ QOC$, we get $y=2.59 m$
Therefore, $PQ = 5+2.59+1.19 = 8.78 \approx\ 8.8 m$
Hence, Option A is the correct answer.
Question 4: Points E, F, G, H lie on the sides AB, BC, CD, and DA, respectively, of a square ABCD. If EFGH is also a square whose area is 62.5% of that of ABCD and CG is longer than EB, then the ratio of length of EB to that of CG is
a) 3 : 8
b) 2 : 5
c) 4 : 9
d) 1 : 3
4) Answer (D)
Solution:
It is given that EFGH is also a square whose area is 62.5% of that of ABCD. Let us assume that E divides AB in x : 1. Because of symmetry we can se that points F, G and H divide BC, CD and DA in x : 1.
Let us assume that ‘x+1’ is the length of side of square ABCD.

Area of square ABCD = $(x+1)^2$ sq. units.
Therefore, area of square EFGH = $\dfrac{62.5}{100}*(x+1)^2$ = $\dfrac{5(x+1)^2}{8}$ … (1)
In right angle triangle EBF,
$EF^2 = EB^2 + BF^2$
$\Rightarrow$ $EF = \sqrt{1^2+x^2}$
Therefore, the area of square EFGH = $EF^2$ = $x^2+1$ … (2)
By equating (1) and (2),
$x^2+1 = \dfrac{5(x+1)^2}{8}$
$\Rightarrow$ $8x^2+8 = 5x^2+10x+5$
$\Rightarrow$ $3x^2-10x+3 = 0$
$\Rightarrow$ $(x – 3)(3x – 1) = 0$
$\Rightarrow$ $x = 3$ or $1/3$
The ratio of length of EB to that of CG = 1 : x
EB : CG = 1 : 3 or 3 : 1. Hence, option D is the correct answer.
Question 5: On a rectangular metal sheet of area 135 sq in, a circle is painted such that the circle touches two opposite sides. If the area of the sheet left unpainted is two-thirds of the painted area then the perimeter of the rectangle in inches is
a) $3\sqrt{\pi}(5+\frac{12}{\pi})$
b) $4\sqrt{\pi}(3+\frac{9}{\pi})$
c) $3\sqrt{\pi}(\frac{5}{2}+\frac{6}{\pi})$
d) $5\sqrt{\pi}(3+\frac{9}{\pi})$
5) Answer (A)
Solution:
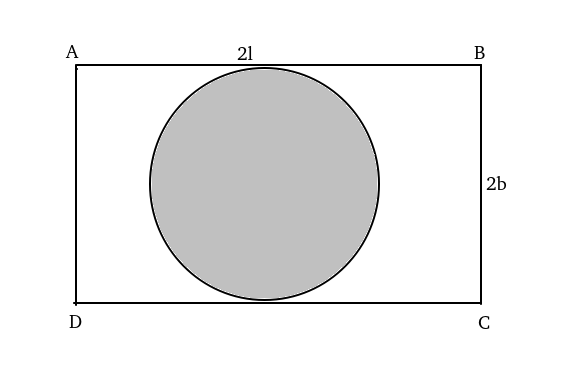
Let ABCD be the rectangle with length 2l and breadth 2b respectively.
Area of the circle i.e. area of painted region = $\pi\ b^2$.
Given, 4lb-$\pi\ b^2$=(2/3)$\pi\ b^2$.
=> 4lb=(5/3)$\pi\ b^2$.
=>l=$\frac{5\pi}{12}b$.
Given, 4lb=135 => 4*$\frac{5\pi}{12}b^2$=135 => b= $\frac{9}{\sqrt{\ \pi\ }}$
=> l=$\frac{15}{4}\sqrt{\ \pi\ }$
Perimeter of rectangle =4(l+b)=4($\frac{15}{4}\sqrt{\ \pi\ }$+$\frac{9}{\sqrt{\ \pi\ }}$ )=$3\sqrt{\pi}(5+\frac{12}{\pi})$.
Hence option A is correct.
Question 6: The shortest distance of the point $(\frac{1}{2},1)$ from the curve y = I x -1I + I x + 1I is
a) 1
b) 0
c) $\sqrt{2}$
d) $\sqrt{\frac{3}{2}}$
6) Answer (A)
Solution:
The graph of the given function is as shown below.

We can see that the shortest distance of the point (1/2, 1) will be 1 unit.
Question 7: The sum of the perimeters of an equilateral triangle and a rectangle is 90cm. The area, T, of the triangle and the area, R, of the rectangle, both in sq cm, satisfying the relationship $R=T^{2}$. If the sides of the rectangle are in the ratio 1:3, then the length, in cm, of the longer side of the rectangle, is
a) 27
b) 21
c) 24
d) 18
7) Answer (A)
Solution:
Let the sides of the rectangle be “a” and “3a” m. Hence the perimeter of the rectangle is 8a.
Let the side of the equilateral triangle be “m” cm. Hence the perimeter of the equilateral triangle is “3m” cm. Now we know that 8a+3m=90……(1)
Moreover area of the equilateral triangle is $\frac{\sqrt{\ 3}}{4}m^2$ and area of the rectangle is $3a^2$
According to the relation given $\left(\frac{\sqrt{\ 3}}{4}m^2\right)^{^2}=\ 3a^2$
$\frac{3}{16}m^4=\ 3a^2\ or\ a^2=\frac{m^4}{16}$
$a=\frac{m^2}{4}$
Substituting this in (1) we get $2m^2+3m-90\ =0$ solving this we get m=6 (ignoring the negative value since side can’t be negative)
Hence a=9 and the longer side of the rectangle will be 3a=27cm
Question 8: AB is a diameter of a circle of radius 5 cm. Let P and Q be two points on the circle so that the length of PB is 6 cm, and the length of AP is twice that of AQ. Then the length, in cm, of QB is nearest to
a) 9.3
b) 7.8
c) 9.1
d) 8.5
8) Answer (C)
Solution:
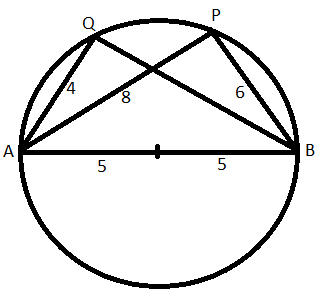
Since AB is a diameter, AQB and APB will right angles.
In right triangle APB, AP = $\sqrt{10^2-6^2}=8$
Now, 2AQ=AP => AQ= 8/2=4
In right triangle AQB, AP = $\sqrt{10^2-4^2}=9.165$ =9.1 (Approx)
Question 9: Two circles, each of radius 4 cm, touch externally. Each of these two circles is touched externally by a third circle. If these three circles have a common tangent, then the radius of the third circle, in cm, is
a) $\frac{1}{\surd2}$
b) $\frac{\pi}{3}$
c) $\surd2$
d) 1
9) Answer (D)
Solution:
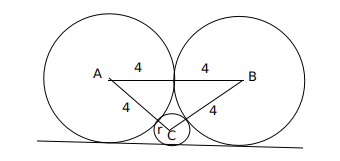
Let ‘h’ be the height of the triangle ABC, semiperimeter(S) $= \frac{4+4+r+4+4+r}{2} = 8+r$,
$a=4+r, b=4+r, c=8$
Area of triangle ABC $=\ \ \sqrt{\ s\cdot\left(s-a\right)\left(s-b\right)\left(s-c\right)}=$
$= \sqrt{\left(\ 8+r\right)\times\ 4\times\ 4\times\ r}$ = $\ \frac{\ 1}{2}\times\ \left(4+4\right)\times\ height$
Height (h) = $\sqrt{\ \left(8+r\right)r}$
Now, $ h + r = 4 \longrightarrow \sqrt{\ \left(8+r\right)r} + r = 4$ (Considering the height of the triangle)
$\sqrt{\ \left(8+r\right)r}$=4-r
16r=16
r=1
Alternatively,
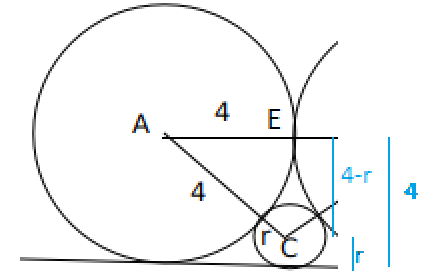
$\text{AE}^@+\text{EC}^2=\text{AC}^2 \longrightarrow 4^2+\left(4-r\right)^2 = \left(4+r\right)^2 \longrightarrow\ \longrightarrow\ \longrightarrow\ r=1$
Question 10: The points (2,1) and (-3,-4) are opposite vertices of a parallelogram.If the other two vertices lie on the line $x+9y+c=0$, then c is
a) 12
b) 13
c) 15
d) 14
10) Answer (D)
Solution:
The midpoints of two diagonals of a parallelogram are the same
Hence the midpoint of (2,1) and (-3,-4) lie on $x+9y+c=0$
midpoint of (2,1) and (-3,-4) = ($\frac{2-3}{2},\frac{1-4}{2}$) = (-1/2 , -3/2)
Keeping this cordinates in the above line equation, we get c = 14
Question 11: The vertices of a triangle are (0,0), (4,0) and (3,9). The area of the circle passing through these three points is
a) $\frac{14\pi}{3}$
b) $\frac{123\pi}{7}$
c) $\frac{12\pi}{5}$
d) $\frac{205\pi}{9}$
11) Answer (D)
Solution:
Equation of circle $x^2+y^2+2gx+2fy+c=0$
It passes through (0,0), (4,0) and (3,9). Substitute each point in the above equation:
=> On substituting the value (0,0) in the above equation, we obtain: $c=0$
=> On substituting the value (4,0) in the above equation, we obtain: $16+0+8g+0 = 0$ ; $g=-2$
=> On substituting the value (3,9) in the above equation, we obtain: $9+81-12+18f = 0$ ; $f= -13/3$
Radius of the circle r = $\sqrt{\ g^2+f^2-c}$ => $r^2=\frac{205}{9}$
Therefore, Area = $\pi\ r^2=\frac{205\pi\ }{9}$
Question 12: A triangle ABC has area 32 sq units and its side BC, of length 8 units, lies on the line x = 4. Then the shortest possible distance between A and the point (0,0) is
a) $8$ units
b) $4$ units
c) $2\sqrt{2}$ units
d) $4\sqrt{2}$ units
12) Answer (B)
Solution:
We know that area of the triangle = 32 sq. units, BC = 8 units
Therefore, the height of the perpendicular drawn from point A to BC = 2*32/8 = 8 units.
Let us draw a possible diagram of the given triangle.
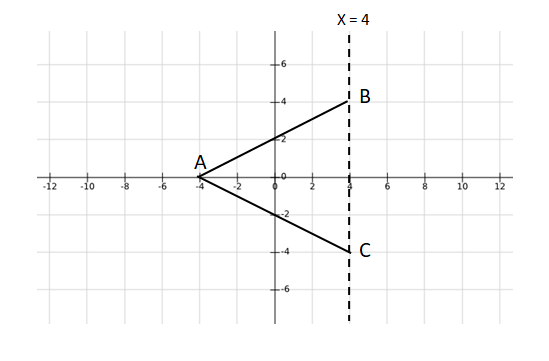
We can see that if A coincide with (-4, 0) then the distance between A and (0, 0) = 4 units.
If we move the triangle up or down keeping the base BC on x = 4, then point A will move away from origin as vertical distance will come into factor whereas horizontal distance will remain as 4 units.
Hence, we can say that minimum distance between A and origin (0, 0) = 4 units.
Question 13: Let A and B be two regular polygons having a and b sides, respectively. If b = 2a and each interior angle of B is $\frac{3}{2}$ times each interior angle of A, then each interior angle, in degrees, of a regular polygon with a + b sides is
Question 14: In a triangle ABC, medians AD and BE are perpendicular to each other, and have lengths 12 cm and 9 cm, respectively. Then, the area of triangle ABC, in sq cm, is
a) 78
b) 80
c) 72
d) 68
14) Answer (C)
Solution:
It is given that AD and BE are medians which are perpendicular to each other.
The lengths of AD and BE are 12cm and 9cm respectively.
It is known that the centroid G divides the median in the ratio of 2:1
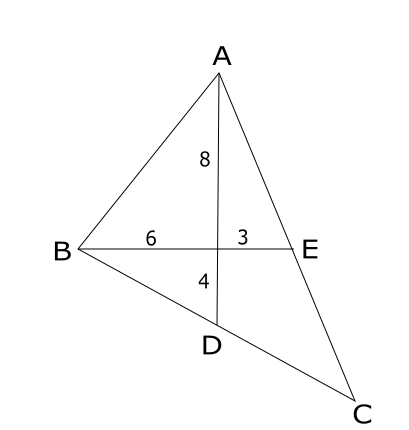
Area of $\triangle$ ABC = 2* Area of the triangle ABD
Area of $\triangle\ $ABD = Area of $\triangle\ $ AGB + Area of $\triangle\ $ BGD
Since $\angle\ AGB\ =\ \angle\ BGD\ =\ 90$ (Given)
Area of $\triangle\ $ AGB = $\ \frac{\ 1}{2}\times\ 8\times\ 6$ = 24
Area of $\triangle\ $ BGD = $\ \frac{\ 1}{2}\times\ 6\times\ 4$ = 12
Area of $\triangle\ $ABD = 24+12=36
Area of $\triangle\ ABC\ =\ 2\times\ 36=72$
Question 15: Let ABC be a right-angled triangle with hypotenuse BC of length 20 cm. If AP is perpendicular on BC, then the maximum possible length of AP, in cm, is
a) 10
b) 5
c) $8\surd2$
d) $6\surd2$
15) Answer (A)
Solution:
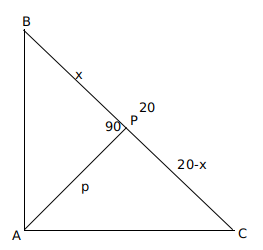
Let p be the length of AP.
It is given that $\angle\ BAC\ =90\ $ and $\angle\ APC\ =90\ $
Let $\angle\ ABC\ =\theta\ $, then $\angle\ BAP\ =90-\theta\ $ and $\angle\ BCA\ =90-\theta\ $
So $\angle\ PAC\ =\theta\ $
Triangles BPA and APC are similar
$p^2=x\left(20-x\right)$
We have to maximize the value of p, which will be maximum when x=20-x
x=10
Question 16: If the rectangular faces of a brick have their diagonals in the ratio $3 : 2 \surd3 : \surd{15}$, then the ratio of the length of the shortest edge of the brick to that of its longest edge is
a) $\sqrt{3} : 2$
b) $1 : \sqrt{3}$
c) $2 : \sqrt{5}$
d) $\sqrt{2} : \sqrt{3}$
16) Answer (B)
Solution:
Assuming the dimensions of the brick are a, b and c and the diagonals are 3, 2 $\surd3$ and $\surd{15}$
Hence, $a^{2\ }+\ b^2$ = $3^2$ ……(1)
$b^{2\ }+\ c^2$ = $(2\sqrt{3})^2$ ……(2)
$c^{2\ }+\ a^2$ = $(\sqrt{15})^2$ ……(3)
Adding the three equations, 2($a^2+b^2+c^2$) = 9+12+15=36
=>$a^2+b^2+c^2$ = 18……(4)
Subtracting (1) from (4), we get $c^2$ = 9 =>c=3
Subtracting (2) from (4), we get $a^2$ = 6 =>a=$\sqrt{6}$
Subtracting (3) from (4), we get $b^2$ = 3 =>b=$\sqrt{3}$
The ratio of the length of the shortest edge of the brick to that of its longest edge is = $\ \frac{\ \sqrt{3}}{3}$ = $1 : \sqrt{3}$
Question 17: Let ABCDEF be a regular hexagon with each side of length 1 cm. The area (in sq cm) of a square with AC as one side is
a) $3\sqrt{2}$
b) $3$
c) $4$
d) $\sqrt{3}$
17) Answer (B)
Solution:
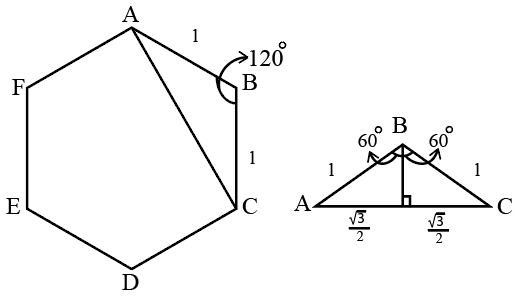
The length of the diagonals of a regular hexagon with side s are $\sqrt{3}s$.
Here length of AC =
$\sqrt{3}s$ = $\sqrt{3}$ cms
Hence area of the square = $\sqrt{3}^2$ = 3 sq cm
Question 18: If three sides of a rectangular park have a total length 400 ft, then the area of the park is maximum when the length (in ft) of its longer side is
Question 19: On a triangle ABC, a circle with diameter BC is drawn, intersecting AB and AC at points P and Q, respectively. If the lengths of AB, AC, and CP are 30 cm, 25 cm, and 20 cm respectively, then the length of BQ, in cm, is
Question 20: A parallelogram ABCD has area 48 sqcm. If the length of CD is 8 cm and that of AD is s cm, then which one of the following is necessarily true?
a) $s≠6$
b) $s \geq 6$
c) $5 \leq s \leq 7$
d) $s \leq 6$
20) Answer (B)
Solution:
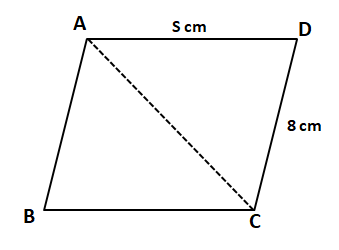
We can see that area of parallelogram ABCD = 2*Area of triangle ACD
48 = 2*Area of triangle ACD
Area of triangle ACD = 24
$(1/2)*CD*DA*sinADC=24$
$AD*sinADC=6$
We know that $sin\theta$ $\leq$ 1, Hence, we can say that AD $\geq$ 6
$\Rightarrow$ s $\geq$ 6
Question 21: The base of a vertical pillar with uniform cross section is a trapezium whose parallel sides are of lengths 10 cm and 20 cm while the other two sides are of equal length. The perpendicular distance between the parallel sides of the trapezium is 12 cm. If the height of the pillar is 20 cm, then the total area, in sq cm, of all six surfaces of the pillar is
a) 1300
b) 1340
c) 1480
d) 1520
21) Answer (C)
Solution:
See the diagram below

Length of side AD = $\sqrt{12^2 + 5^2 } = 13$
Area of the trapezium = 12 * (10 + 20)/2 = 180
Perimeter of the trapezium = 10 + 20 + 13 + 13 = 56
Area of the sides of the pillar = 56 * height = 56 * 20 = 1120.
Total are of the pillar = 1120 + area of base + area of the top = 1120 + 180 + 180 = 1480
Question 22: In a parallelogram ABCD of area 72 sq cm, the sides CD and AD have lengths 9 cm and 16 cm, respectively. Let P be a point on CD such that AP is perpendicular to CD. Then the area, in sq cm, of triangle APD is
a) $32\sqrt{3}$
b) $18\sqrt{3}$
c) $24\sqrt{3}$
d) $12\sqrt{3}$
22) Answer (A)
Solution:
In a parallelogram ABCD of area 72 sq cm, the sides CD and AD have lengths 9 cm and 16 cm, respectively. Let P be a point on CD such that AP is perpendicular to CD. Then the area, in sq cm, of triangle APD is
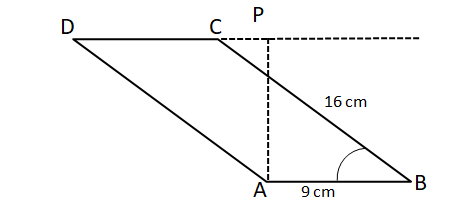
Given that area of parallelogram = 72 sq cm
Area of triangle ABC = $\dfrac{1}{2}$*area of parallelogram
(1/2)*AB*BC*sinABC = $\dfrac{1}{2}$*72
sinABC = $\dfrac{1}{2}$
$\angle$ ABC = 30°
Let us draw a perpendicular CQ from C to AB.
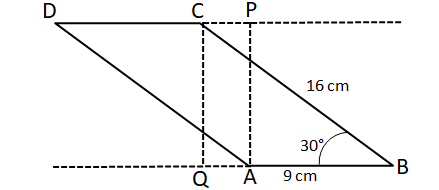
$\angle\ B\ =\ \angle\ D\ =\ 30^{\circ\ }$ ( opposite angles in a parallelogram)
$\angle\ QCB\ =\ \angle\ DAP\ =\ 60^{\circ\ }$ ( Sum of angles in a triangle = 180)
In triangles APD and CQB, AP= CQ , AD=CB ( opposite sides of a parallelogram) , $\angle\ QCB\ =\ \angle\ DAP\ =\ 60^{\circ\ }$
Hence APD and CQB are congruent triangles using SAS property.
Therefore, we can say that area of triangle APD = area of triangle CQB
In right angle triangle CQB,
QB = CBcos30° = $16*\dfrac{\sqrt{3}}{2}$ = $8\sqrt{3}$ cm
CQ = CBsin30° = $16*\dfrac{1}{2}$ = $8$ cm
Therefore, area of triangle CQB = 1/2*CQ*QB = $1/2*8*8\sqrt{3}$ = $32\sqrt{3}$
Hence, we can say that area of triangle APD = $32\sqrt{3}$.
Question 23: In a circle, two parallel chords on the same side of a diameter have lengths 4 cm and 6 cm. If the distance between these chords is 1 cm, then the radius of the circle, in cm, is
a) $\sqrt{13}$
b) $\sqrt{14}$
c) $\sqrt{11}$
d) $\sqrt{12}$
23) Answer (A)
Solution:
Given that two parallel chords on the same side of a diameter have lengths 4 cm and 6 cm.
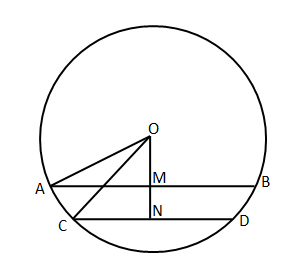
In the diagram we can see that AB = 6 cm, CD = 4 cm and MN = 1 cm.
We can see that M and N are the mid points of AB and CD respectively.
AM = 3 cm and CD = 2 cm. Let ‘OM’ be x cm.
In right angle triangle AMO,
$AO^2 = AM^2 + OM^2$
$\Rightarrow$ $AO^2 = 3^2 + x^2$ … (1)
In right angle triangle CNO,
$CO^2 = CN^2 + ON^2$
$\Rightarrow$ $CO^2 = 2^2 + (OM+MN)^2$
$\Rightarrow$ $CO^2 = 2^2 + (x+1)^2$ … (2)
We know that both AO and CO are the radius of the circle. Hence $AO = CO$
Therefore, we can equate equation (1) and (2)
$3^2+x^2$=$2^2+(x+1)^2$
$\Rightarrow$ x = 2 cm
Therefore, the radius of the circle
$AO = \sqrt{AM^2 + OM^2}$
$\Rightarrow$ $AO=\sqrt{3^2+2^2}=\sqrt{13}$. Hence, option A is the correct answer.
Question 24: ABCD is a quadrilateral inscribed in a circle with centre O such that O lies inside the quadrilateral. If $\angle COD = 120$ degrees and $\angle BAC = 30$ degrees, then the value of $\angle BCD$ (in degrees) is
Question 25: Given an equilateral triangle T1 with side 24 cm, a second triangle T2 is formed by joining the midpoints of the sides of T1. Then a third triangle T3 is formed by joining the midpoints of the sides of T2. If this process of forming triangles is continued, the sum of the areas, in sq cm, of infinitely many such triangles T1, T2, T3,… will be
a) $188\sqrt{3}$
b) $248\sqrt{3}$
c) $164\sqrt{3}$
d) $192\sqrt{3}$
25) Answer (D)
Solution:
We can see that T$_{2}$ is formed by using the mid points of T$_{1}$. Hence, we can say that area of triangle of T$_{2}$ will be (1/4)th of the area of triangle T$_{1}$.
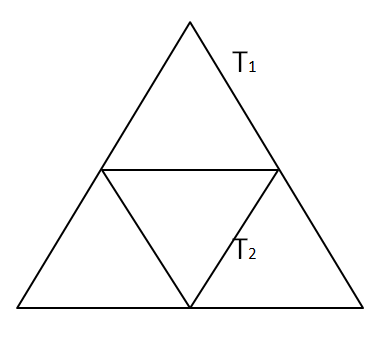
Area of triangle T$_{1}$ = $\dfrac{\sqrt{3}}{4}*(24)^2$ = $144\sqrt{3}$ sq. cm
Area of triangle T$_{2}$ = $\dfrac{144\sqrt{3}}{4}$ = $36\sqrt{3}$ sq. cm
Sum of the area of all triangles = T$_{1}$ + T$_{2}$ + T$_{3}$ + …
$\Rightarrow$ T$_{1}$ + T$_{1}$/$4$ + T$_{1}$/$4^2$ + …
$\Rightarrow$ $\dfrac{T_{1}}{1 – 0.25}$
$\Rightarrow$ $\dfrac{4}{3}*T_{1}$
$\Rightarrow$ $\dfrac{4}{3}*144\sqrt{3}$
$\Rightarrow$ $192\sqrt{3}$
Hence, option D is the correct answer.
Question 26: The points (2, 5) and (6, 3) are two end points of a diagonal of a rectangle. If the other diagonal has the equation y =3x+c,then c is
a) -5
b) -6
c) -7
d) -8
26) Answer (D)
Solution:
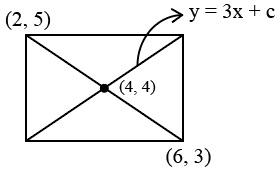
The midpoint of one diagonal lies on the other diagonal.
Midpoint is ((2+6)/2, (5+3)/2) = (4,4)
Hence 4 = 3 * 4 + c => c = -8
Question 27: From an interior point of an equilateral triangle, perpendiculars are drawn on all three sides. The sum of the lengths of the three perpendiculars is s. Then the area of the triangle is
a) $\frac{\sqrt{3}s^{2}}{2}$
b) $\frac{2s^{2}}{\sqrt{3}}$
c) $\frac{s^{2}}{2\sqrt{3}}$
d) $\frac{s^{2}}{\sqrt{3}}$
27) Answer (D)
Solution:
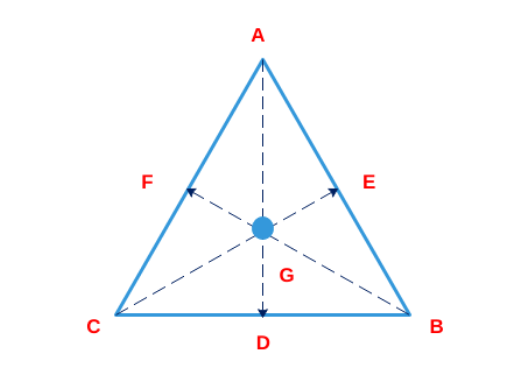
Based on the question: AD, CE and BF are the three altitudes of the triangle. It has been stated that {GD+GE+GF = s}
Now since the triangle is equilateral, let the length of each side be “a”. So area of triangle will be
$\frac{1}{2}\times\ GD\times\ a+\ \frac{1}{2}\times\ GE\times\ a\ +\frac{1}{2}\times\ GF\times\ a=\frac{\sqrt{\ 3}}{4}a^2$
Now $GD+GE+GF=\frac{\sqrt{\ 3}a}{2}$ or $s=\frac{\sqrt{\ 3}a}{2}\ or\ a=\frac{2s}{\sqrt{\ 3}}$
Given the area of the equilateral triangle = $\ \frac{\sqrt{3}}{4}a^2\ $ ; substituting the value of ‘a’ from above, we get the area {in terms ‘s’}= $\frac{s^2}{\sqrt{3}}$
Question 28: A man makes complete use of 405 cc of iron, 783 cc of aluminium, and 351 cc of copper to make a number of solid right circular cylinders of each type of metal. These cylinders have the same volume and each of these has radius 3 cm. If the total number of cylinders is to be kept at a minimum, then the total surface area of all these cylinders, in sq cm, is
a) $1026(1 + \pi)$
b) $8464\pi$
c) $928\pi$
d) $1044(4 + \pi)$
28) Answer (A)
Solution:
It is given that the volume of all the cylinders is the same, so the volume of each cylinder = HCF of (405, 783, 351)
=27
The number of iron cylinders = $\ \frac{\ 405}{27}$ = 15
The number of aluminium cylinders = $\ \frac{\ 783}{27}$ = 29
The number of copper cylinders = $\ \frac{351\ }{27}$ = 13
15*$\pi\ r^2h=$ 405
15*$\pi\ 9*h=$ 405
$\pi\ h=3$
Now we have to calculate the total surface area of all the cylinders
Total number of cylinders = 15+29+13 = 57
Total surface area of the cylinder = 57*($2\pi\ rh+2\pi\ r^2$)
=57(2*3*3 + 2*9*$\pi\ $)
=$1026(1 + \pi)$
Question 29: A right circular cone, of height 12 ft, stands on its base which has diameter 8 ft. The tip of the cone is cut off with a plane which is parallel to the base and 9 ft from the base. With $\pi$ = 22/7, the volume, in cubic ft, of the remaining part of the cone is
Question 30: A ball of diameter 4 cm is kept on top of a hollow cylinder standing vertically. The height of the cylinder is 3 cm, while its volume is $9\pi$ cubic centimeters. Then the vertical distance, in cm, of the topmost point of the ball from the base of the cylinder is
Question 31: Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC. Let BPC be an arc of a circle centered at A and lying between BC and BQC. If AB has length 6 cm then the area, in sq cm, of the region enclosed by BPC and BQC is
a) $9\pi-18$
b) 18
c) $9\pi$
d) 9
31) Answer (B)
Solution:
The image of the figure is as shown.

AB = AC = 6cm. Thus, BC = $\sqrt{6^2 + 6^2}$ = 6√2 cm
The required area = Area of semi-circle BQC – Area of quadrant BPC + Area of triangle ABC
Area of semicircle BQC
Diameter BC = 6√2cm
Radius = 6√2/2 = 3√2 cm
Area = $\pi r^2 $/2 = $ \pi$ * $(3 \sqrt{2})^2 $/2 = 9$\pi$
Area of quadrant BPC
Area = $\pi r^2$/4 = $\pi*(6)^2$/4 = 9$\pi$
Area of triangle ABC
Area = 1/2 * 6 * 6 = 18
The required area = Area of semi-circle BQC – Area of quadrant BPC + Area of triangle ABC
= 9$\pi$ – 9$\pi$ + 18 = 18
Question 32: The area of a rectangle and the square of its perimeter are in the ratio 1 ∶ 25. Then the lengths of the shorter and longer sides of the rectangle are in the ratio
a) 1:4
b) 2:9
c) 1:3
d) 3:8
32) Answer (A)
Solution:
Let ‘a’ and ‘b’ be the length of sides of the rectangle. (a > b)
Area of the rectangle = a*b
Perimeter of the rectangle = 2*(a+b)
$\Rightarrow$ $\dfrac{a*b}{(2*(a+b))^2}=\dfrac{1}{25}$
$\Rightarrow$ $25ab=4(a+b)^2$
$\Rightarrow$ $4a^2-17ab+4b^2=0$
$\Rightarrow$ $(4a-b)(a-4b)=0$
$\Rightarrow$ $a = 4b$ or $\dfrac{b}{4}$
We initially assumed that a > b, therefore a $\neq$ $\dfrac{b}{4}$.
Hence, a = 4b
$\Rightarrow$ b : a = 1 : 4
Question 33: From a triangle ABC with sides of lengths 40 ft, 25 ft and 35 ft, a triangular portion GBC is cut off where G is the centroid of ABC. The area, in sq ft, of the remaining portion of triangle ABC is
a) $225\sqrt{3}$
b) $\frac{500}{\sqrt{3}}$
c) $\frac{275}{\sqrt{3}}$
d) $\frac{250}{\sqrt{3}}$
33) Answer (B)
Solution:
The lengths are given as 40, 25 and 35.
The perimeter = 100
Semi-perimeter, s = 50
Area = $ \sqrt{50 * 10 * 25 * 15}$ = $250\sqrt{3}$
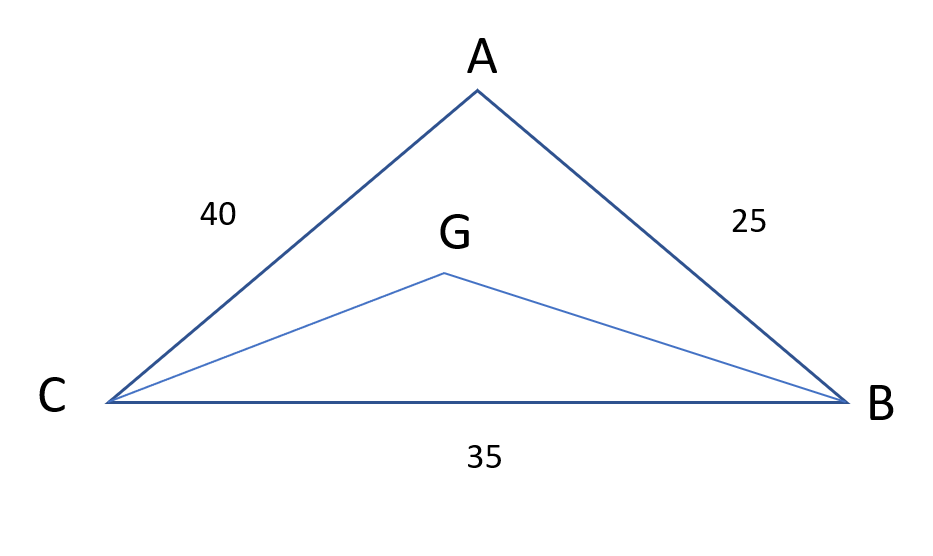
The triangle formed by the centroid and two vertices is removed.
Since the cenroid divides the median in the ratio 2 : 1
The remaining area will be two-thirds the area of the original triangle.
Remaining area = $\frac{2}{3} * 250\sqrt{3}$ = $\frac{500}{\sqrt{3}}$
Question 34: In a circle of radius 11 cm, CD is a diameter and AB is a chord of length 20.5 cm. If AB and CD intersect at a point E inside the circle and CE has length 7 cm, then the difference of the lengths of BE and AE, in cm, is
a) 2.5
b) 1.5
c) 3.5
d) 0.5
34) Answer (D)
Solution:

In figure AE*BE=CE*DE (The intersecting chords theorem)
=> 7*15= x(20.5-x) (Assuming AE=x)
=> 210=x(41-2x)
=> $2x^2$-41x+210=0
=> x=10 or x=10.5 => AE=10 or AE=10.5 Hence BE = 20.5-10=10.5 or BE = 20.5-10.5=10
Required difference= 10.5-10=0.5
Question 35: A chord of length 5 cm subtends an angle of 60° at the centre of a circle. The length, in cm, of a chord that subtends an angle of 120° at the centre of the same circle is
a) $5\sqrt{3}$
b) $2\pi$
c) $8$
d) $6\sqrt{2}$
35) Answer (A)
Solution:
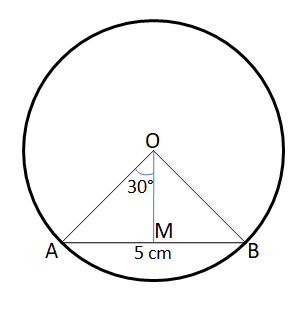
We are given that AB = 5 cm and $\angle$ AOB = 60°
Let us draw OM such that OM $\perp$ AB.
In right angle triangle AMO,
$sin 30° = \dfrac{AM}{AO}$
$\Rightarrow$ AO = 2*AM = 2*2.5 = 5 cm. Therefore, we can say that the radius of the circle = 5 cm.
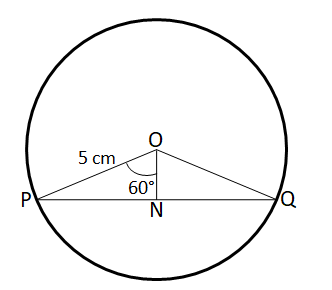
In right angle triangle PNO,
$sin 60° = \dfrac{PN}{PO}$
$\Rightarrow$ PN = $\dfrac{\sqrt{3}}{2}$*PO = $\dfrac{5\sqrt{3}}{2}$
Therefore, PQ = 2*PN = $5\sqrt{3}$ cm
Question 36: Corners are cut off from an equilateral triangle T to produce a regular hexagon H. Then, the ratio of the area of H to the area of T is
a) 2 : 3
b) 4 : 5
c) 5 : 6
d) 3 : 4
36) Answer (A)
Solution:
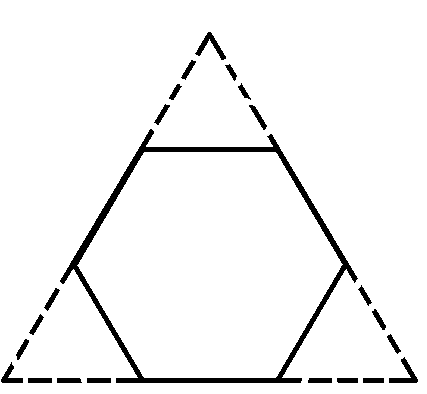
The given figure can be divided into 9 regions or equilateral triangles of equal areas as shown below,
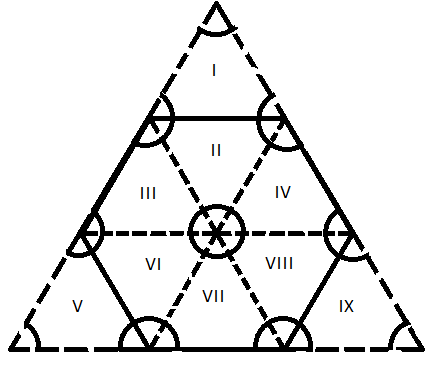
Now the hexagon consists of 6 regions and the triangle consists of 9 regions.
Hence the ratio of areas = 6/9 =2:3
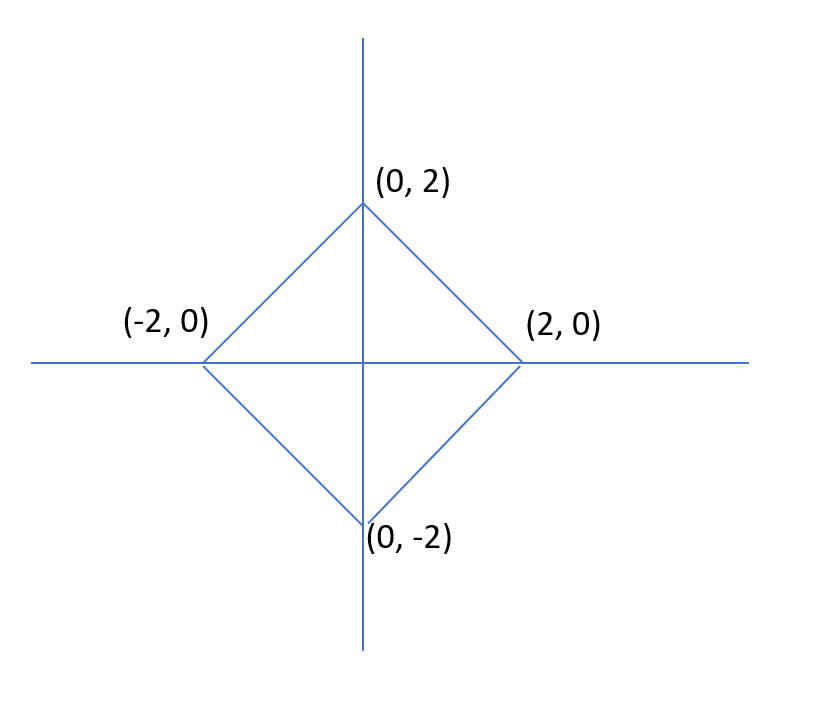
Question 37: The area of the closed region bounded by the equation I x I + I y I = 2 in the two-dimensional plane is
a) $4\pi$ sq. units
b) 4 sq. units
c) 8 sq. units
d) $2\pi$ sq. units
37) Answer (C)
Solution:
The following equation will form a square of side $ 2\sqrt{2} $.
The area of the square = $(2\sqrt{2})^2$ = 8 units.
Question 38: Let C1 and C2 be concentric circles such that the diameter of C1 is 2cm longer than that of C2. If a chord of C1 has length 6cm and is a tangent to C2, then the diameter, in cm, of C1 is
Question 39: In a circle with center O and radius 1 cm, an arc AB makes an angle 60 degrees at O. Let R be the region bounded by the radii OA, OB and the arc AB. If C and D are two points on OA and OB, respectively, such that OC = OD and the area of triangle OCD is half that of R, then the length of OC, in cm, is
a) $ (\frac{\pi}{4\sqrt{3}})^{\frac{1}{2}}$
b) $(\frac{\pi}{6})^{\frac{1}{2}}$
c) $(\frac{\pi}{3\sqrt{3}})^{\frac{1}{2}}$
d) $(\frac{\pi}{4})^{\frac{1}{2}}$
39) Answer (C)
Solution:
It is given that radius of the circle = 1 cm
Chord AB subtends an angle of 60° on the centre of the given circle. R be the region bounded by the radii OA, OB and the arc AB.
Therefore, R = $\dfrac{60°}{360°}$*Area of the circle = $\dfrac{1}{6}$*$\pi*(1)^2$ = $\dfrac{\pi}{6}$ sq. cm
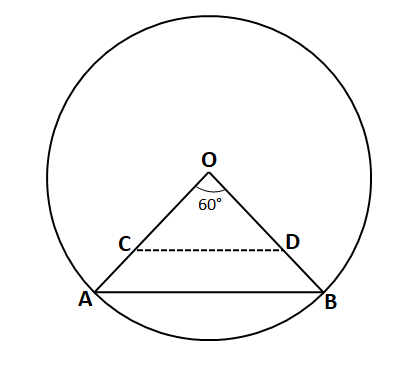
It is given that OC = OD and area of triangle OCD is half that of R. Let OC = OD = x.
Area of triangle COD = $\dfrac{1}{2}*OC*OD*sin60°$
$\dfrac{\pi}{6*2}$ = $\dfrac{1}{2}*x*x*\dfrac{\sqrt{3}}{2}$
$\Rightarrow$ $x^2 = \dfrac{\pi}{3\sqrt{3}}$
$\Rightarrow$ $x$ = $(\frac{\pi}{3\sqrt{3}})^{\frac{1}{2}}$ cm. Hence, option C is the correct answer.
Question 40: Let ABC be a right-angled triangle with BC as the hypotenuse. Lengths of AB and AC are 15 km and 20 km, respectively. The minimum possible time, in minutes, required to reach the hypotenuse from A at a speed of 30 km per hour is
Question 41: The base of a regular pyramid is a square and each of the other four sides is an equilateral triangle, length of each side being 20 cm. The vertical height of the pyramid, in cm, is
a) 12
b) $10\surd2$
c) $8\surd3$
d) $5\surd5$
41) Answer (B)
Solution:
It is given that the base of the pyramid is square and each of the four sides are equilateral triangles.
Length of each side of the equilateral triangle = 20cm
Since the side of the triangle will be common to the square as well, the side of the square = 20cm
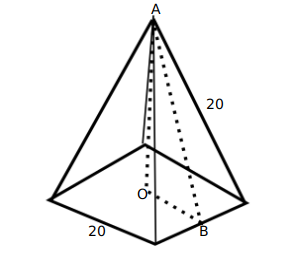
Let h be the vertical height of the pyramid ie OA
OB = 10 since it is half the side of the square
AB is the height of the equilateral triangle i.e 10$\sqrt{\ 3}$
AOB is a right angle, so applying the Pythagorean formula, we get
$OA^2+ OB^2= AB^2$
$h^2$ + 100= 300
h=10$\sqrt{\ 2}$
Question 42: Let ABCD be a rectangle inscribed in a circle of radius 13 cm. Which one of the following pairs can represent, in cm, the possible length and breadth of ABCD?
a) 24, 10
b) 25, 9
c) 25, 10
d) 24, 12
42) Answer (A)
Solution:
Let ABCD be a rectangle inscribed in a circle of radius 13 cm. Which one of the following pairs can represent, in cm, the possible length and breadth of ABCD?
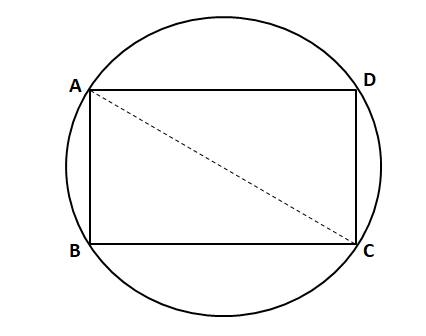
We know that AC is the diameter and $\angle$ ABC = 90°. AC = 2*13 = 26 cm
In right angle triangle ABC,
$AC^2 = AB^2 + BC^2$
$\Rightarrow$ $AB^2+BC^2=26^2$
$\Rightarrow$ $AB^2+BC^2=676$
Let us check with the options.
Option (A): $24^2+10^2 = 676$. Hence, this is a possible answer.
Option (B): $25^2+9^2 = 706 \neq 676$. Hence, this is an incorrect pair.
Option (C): $25^2+10^2 = 725 \neq 676$. Hence, this is an incorrect pair.
Option (D): $24^2+12^2 = 720 \neq 676$. Hence, this is an incorrect pair.
Therefore, we can say that option A is the correct answer.
Question 43: A solid metallic cube is melted to form five solid cubes whose volumes are in the ratio 1 : 1 : 8 : 27 : 27. The percentage by which the sum of the surface areas of these five cubes exceeds the surface area of the original cube is nearest to
a) 10
b) 50
c) 60
d) 20
43) Answer (B)
Solution:
Let the volumes of the five cubes be x, x, 8x, 27x and 27x.
Let the sides be a, a, 2a, 3a and 3a. ($x = a^3$)
Let the side of the original cube be A.
$A^3 = x + x + 8x + 27x + 27x$
$A = 4a$
Original surface area = $96a^2$
New surface area = $6(a^2 + a^2 + 4a^2 + 9a^2 + 9a^2)$ = $144a^2$
Percentage increase = $\frac{144 – 96}{96}*100 =$ 50%
Question 44: Let P be an interior point of a right-angled isosceles triangle ABC with hypotenuse AB. If the perpendicular distance of P from each of AB,BC,and CA is $4(\sqrt{2}-1)$ cm,then the area, in sq cm, of the triangle ABC is
Question 45: Let T be the triangle formed by the straight line 3x + 5y – 45 = 0 and the coordinate axes. Let the circumcircle of T have radius of length L, measured in the same unit as the coordinate axes. Then, the integer closest to L is
Question 46: From a rectangle ABCD of area 768 sq cm, a semicircular part with diameter AB and area 72π sq cm is removed. The perimeter of the leftover portion, in cm, is
a) 80 + 16π
b) 86 + 8π
c) 88 + 12π
d) 82 + 24π
46) Answer (C)
Solution:
Area of the semicircle with AB as a diameter = $\dfrac{1}{2}*\pi*(\dfrac{AB^2}{4})$
$\Rightarrow$ $\dfrac{1}{2}*\pi*(\dfrac{AB^2}{4})$ = $72*\pi$
$\Rightarrow$ $AB = 24 cm$
Given that area of the rectangle ABCD = 768 sq.cm
$\Rightarrow$ AB*BC = 768
$\Rightarrow$ BC = 32 cm

We can see that the perimeter of the remaining shape = AD + DC + BC + Arc(AB)
$\Rightarrow$ 32+24+32+$\pi*24/2$
$\Rightarrow$ $88+12\pi$
Question 47: In a trapezium $ABCD$, $AB$ is parallel to $DC$, $BC$ is perpendicular to $DC$ and $\angle BAD=45^{0}$. If $DC$ = 5cm, $BC$ = 4 cm,the area of the trapezium in sq cm is
Question 48: Let ABCD be a parallelogram. The lengths of the side AD and the diogonal AC are 10cm and 20cm, respectively. If the angle $\angle ADC$ is equal to $30^{0}$ then the area of the parallelogram, in sq.cm is
a) $\frac{25(\sqrt{5}+\sqrt{15})}{2}$
b) $25(\sqrt{3}+\sqrt{15})$
c) $\frac{25(\sqrt{3}+\sqrt{15})}{2}$
d) ${25(\sqrt{5}+\sqrt{15})}$
48) Answer (B)
Solution:
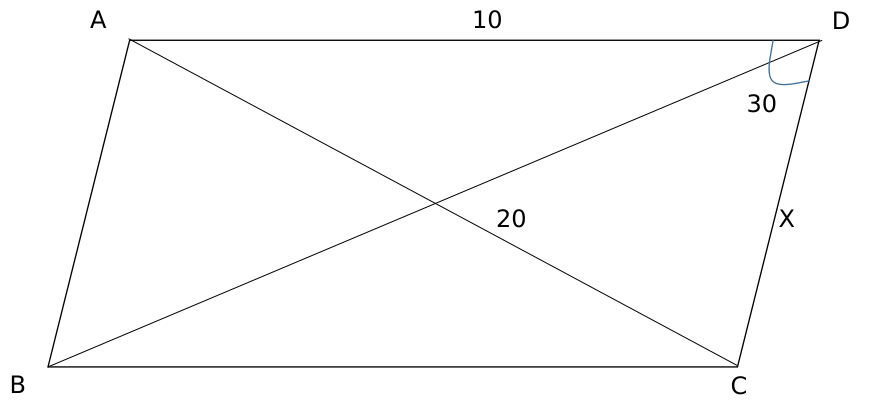
Applying cosine rule in triangle ACD,
$100+X^2-2\times\ 10\times\ X\cos30=400$
$X^2-10X\sqrt{\ 3}-300=0$
Solving, we get X = $\left(\frac{10\sqrt{\ 3}+10\sqrt{\ 15}}{2}\right)$
Hence, area = 10Xsin 30 = $\frac{\left(\frac{10\sqrt{\ 3}+10\sqrt{\ 15}}{2}\right)10}{2}$
= $25(\sqrt{3}+\sqrt{15})$
Question 49: A park is shaped like a rhombus and has area 96 sq m. If 40 m of fencing is needed to enclose the park, the cost, in INR, of laying electric wires along its two diagonals, at the rate of ₹125 per m, is
Question 50: Suppose the length of each side of a regular hexagon ABCDEF is 2 cm.It T is the mid point of CD,then the length of AT, in cm, is
a) $\sqrt{13}$
b) $\sqrt{14}$
c) $\sqrt{12}$
d) $\sqrt{15}$
50) Answer (A)
Solution:
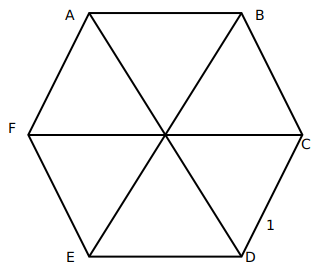
Since a regular hexagon can be considered to be made up of 6 equilateral triangles, a line joining the farthest vertices of a hexagon can be considered to be made up using the sides of two opposite equilateral triangle forming the hexagon. Hence, its length should be twice the side of the hexagon, in this case, 4 cm.
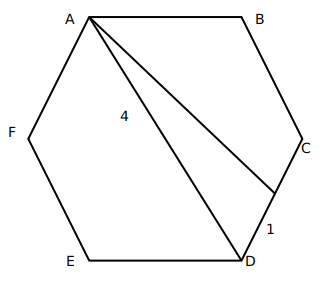
Now, AD divided the hexagon into two symmetrical halves. Hence, AD bisects angle D, and hence, angle ADC is $60^{\circ\ }$.
We can find out the value of AT using cosine formula:
$AT^2=\ 4^2+1^2-2\times\ 1\times\ 4\cos60$
$AT^2=\ 17-4=13$
$AT=\sqrt{\ 13}$
Question 51: Let D and E be points on sides AB and AC, respectively, of a triangle ABC, such that AD : BD = 2 : 1 and AE : CE = 2 : 3. If the area of the triangle ADE is 8 sq cm, then the area of the triangle ABC, in sq cm, is
Question 52: If a triangle ABC, $\angle BCA=50^{0}$. D and E are points on $AB$ and $AC$, respectively, such that $AD=DE$. If F is a point on $BC$ such that $BD=DF$, then $\angle FDE$, in degrees, is equal to
a) 72
b) 80
c) 100
d) 96
52) Answer (B)
Solution:
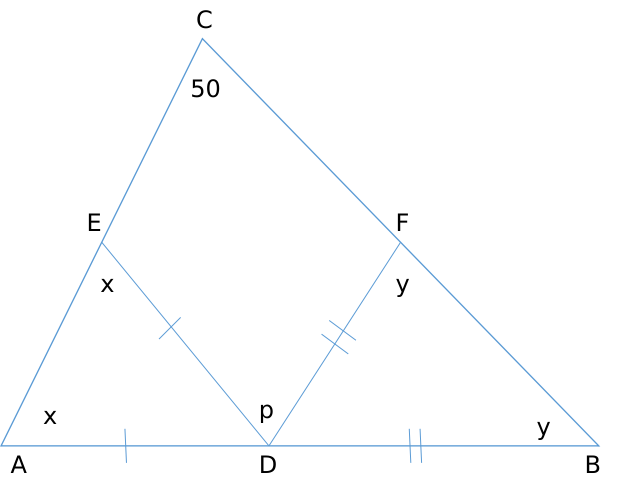
We need to find out p.
Angle ADE = 180 – 2x
Angle BDF = 180 – 2y
Now, 180 – 2y + p + 180 – 2x = 180 [Straight line = 180 deg]
p = 2x + 2y – 180
Also, x + y + 50 = 180 [Sum of the angles of triangle = 180]
x + y = 130
p = 260 – 180 = 80 degrees.
Question 53: The cost of fencing a rectangular plot is ₹ 200 per ft along one side, and ₹ 100 per ft along the three other sides. If the area of the rectangular plot is 60000 sq. ft, then the lowest possible cost of fencing all four sides, in INR, is
a) 120000
b) 90000
c) 100000
d) 160000
53) Answer (A)
Solution:
Let us draw the rectangle.

Now, definitely, three sides should be fenced at Rs 100/ft, and one side should be fenced at Rs 200/ft.
In this question, we are going to assume that the L is greater than B.
Hence, the one side painted at Rs 200/ft should be B to minimise costs.
Hence, the total cost = 200B + 100B + 100L + 100L = 300B + 200L
Now, L x B = 60000
B = 60000/L
Hence, total cost = 300B + 200L = 18000000/L + 200L
To minimise this cost, we can use AM>=GM,
$\frac{\frac{18000000}{L}+200L}{2}\ge\sqrt{\ \frac{18000000}{L}\times\ 200L}$
$\frac{18000000}{L}+200L\ge2\sqrt{\ 18000000\times\ 200}$
$\frac{18000000}{L}+200L\ge2\times\ 60000$
Hence, minimum cost = Rs 120000.
Question 54: If a rhombus has area 12 sq cm and side length 5 cm, then the length, in cm, of its longer diagonal is
a) $\sqrt{37}+\sqrt{13}$
b) $\sqrt{13}+\sqrt{12}$
c) $\frac{\sqrt{37}+\sqrt{13}}{2}$
d) $\frac{\sqrt{13}+\sqrt{12}}{2}$
54) Answer (A)
Solution:
All the sides of the rhombus are equal.
The area of a rhombus is $12\ cm^2$
Considering d1 to be the length of the longer diagonal, d2 to be the length of the shorter diagonal.
The area of a rhombus is $\left(\frac{1}{2}\right)\left(d1\right)\cdot\left(d2\right)\ =\ 12$
d1*d2 = 24.
The length of the side of a rhombus is given by $\frac{\sqrt{\ d1^2+d2^2}}{2}$. This is because the two diagonals and a side from a right-angled triangle with sides d1/2, d2/2 and the side length.
$\frac{\sqrt{\ d1^2+d2^2}}{2}=\ 5$
Hence $\sqrt{\ d1^2+d2^2}\ =\ 10$
$d1^2+d2^2\ =\ 100$
Using d1*d2 = 24, 2*d1*d2 = 48.
$d1^2+d2^2\ +2\cdot d1\cdot d2=\ 100+48\ =\ 148$
$d1^2+d2^2\ -2\cdot d1\cdot d2=\ 100-48\ =\ 52$
$d1+d2\ =\ \sqrt{\ 148}$ (1)
d1-d2 = $\sqrt{52}$ (2)
(1) + (2)= 2*(d1) = 2*($\sqrt{\ 37}+\sqrt{\ 13}$)
d1 = $\sqrt{\ 37}+\sqrt{\ 13}$
or
In a rhombus the area of a Rhombus is given by :
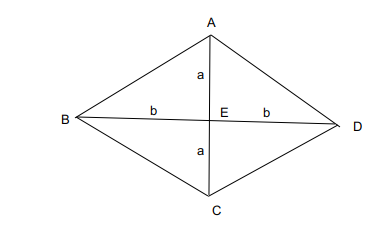
The diagonals perpendicularly bisect each other. Considering the length of the diagonal to be 2a, 2b.
The area of a Rhombus is : $\left(\frac{1}{2}\right)\cdot\left(2a\right)\cdot\left(2b\right)\ =\ 12$
ab =6.
The length of each side is : $\sqrt{\ a^2+b^2}$ = 5, $a^2+b^{2\ }=\ 25,\ $
$\left(a+b\right)^2=\ 37,\ \left(a+b\right)\ =\ \sqrt{\ 37}$
($\left(a-b\right)^2=\ 13,\ a-b\ =\ \sqrt{\ 13}$
$2a\ =\ \left(\sqrt{\ 37}+\sqrt{\ 13}\right)$, $2b\ =\ \left(\sqrt{\ 37}-\sqrt{\ 13}\right)$.
2a is longer diagonal which is equal to $\ \left(\sqrt{\ 37}+\sqrt{\ 13}\right)$
Question 55: A circle of diameter 8 inches is inscribed in a triangle ABC where $\angle ABC = 90^\circ$. If BC = 10 inches then the area of the triangle in square inches is
Question 56: The sides AB and CD of a trapezium ABCD are parallel, with AB being the smaller side. P is the midpoint of CD and ABPD is a parallelogram. If the difference between the areas of the parallelogram ABPD and the triangle BPC is 10 sq cm, then the area, in sq cm, of the trapezium ABCD is
a) 30
b) 40
c) 25
d) 20
56) Answer (A)
Solution:
We are given that :
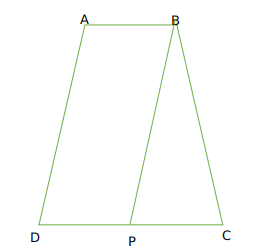
Let DP =x
So AB =x
Now DP=CP
So CD = 2x
Now let height of trapezium be h
we can say A(Parallelogram ABPD ) = xh
And A (BPC) =$\frac{1}{2}xh$
Now by condition$xh-\frac{1}{2}xh=10$
$\frac{xh}{2}=10$
so xh =20
Now therefore area of trapezium ABCD = $\frac{1}{2}\left(x+2x\right)h\ =\ \frac{3}{2}xh\ =\ 30$




![CAT Averages Questions PDF [Important Questions] CAT AVERAGES Questions PDF](https://cracku.in/blog/wp-content/uploads/2022/07/CAT-AVERAGES-Questions-PDF-218x150.png)
