SSC CGL Problems On Triangles
Download SSC CGL Problems on Triangles questions with answers PDF based on previous papers very useful for SSC CGL exams. 20 Very important Problems on Triangles objective questions (MCQ’s) for SSC exams.
Download SSC CGL Problems On Triangles
25 SSC CGL Mocks – Just Rs. 149
Question 1: In a $\triangle$ ABC, D and E are two points on sides AB and AC such that DE is parallel to BC and AD : DB = 2 : 1. If AE = 8 cm, then find the length of AC.
a) 12 cm
b) 10 cm
c) 16 cm
d) 20 cm
Question 2: In a $\triangle$ ABC, Points D and E are on sides AB and AC such that DE is parallel to BC and AD : DB = 3 : 1 and AE = 18 cm. Then find AC.
a) 26 cm
b) 24 cm
c) 28 cm
d) 32 cm
Question 3: In a $\triangle$ ABC, points D and E are on the sides of AB and AC respectively such that DE is parallel to BC and AD : AB = 2 : 5 and AE = 4 cm. Then find AC.
a) 10 cm
b) 14 cm
c) 12 cm
d) 9 cm
Question 4: The coordinates of the vertices of a right-angled triangle are A (6, 2), B(8, 0) and C (2, -2). The coordinates of the orthocentre of triangle PQR are
a) (2, -2)
b) (2, 1)
c) (6, 2)
d) (8, 0)
Question 5: find the area of an equilateral triangle if the height of the triangle is 24 cm.
a) $192\sqrt{3} cm^2$
b) $175\sqrt{3} cm^2$
c) $178\sqrt{3} cm^2$
d) $164\sqrt{3} cm^2$
SSC CGL Previous Papers Download PDF
SSC CHSL PREVIOUS PAPERS DOWNLOAD
Question 6: Three sides of a triangular meadow are of length 28 m, 45 m and 53 m long respectively. Find the cost of sowing seeds(in rupees per sq.m) in the meadow at the rate of 12 rupees per sq.m.
a) 7560
b) 6860
c) 7960
d) 7860
Question 7: In a triangle PQR, internal angular bisectors of $\angle Q$ and $\angle R$ intersect at a point O. If $\angle P$=$110^\circ$ then what is the value of $\angle QOR$ ?
a) $125^\circ$
b) $135^\circ$
c) $145^\circ$
d) $115^\circ$
Question 8: In a triangle XYZ, XA is the angle bisector onto YZ. If the semiperimeter of the triangle is 12 and XY=12 ,YZ=6 then what is the ratio of YA:AZ ?
a) 2:3
b) 2:1
c) 1:2
d) 3:2
Question 9: In a triangle ABC, AX is the angle bisector onto BC. If the semiperimeter of the triangle is 9 and AB=4 ,BC=6 then what is the ratio of BX:XC ?
a) 2:3
b) 2:1
c) 1:2
d) 3:2
Question 10: In an equilateral triangle,if h-R=15 cm where h=height of the triangle and R=circumradius then what is the area of the triangle ?
a) $275\sqrt{3}$
b) $225\sqrt{3}$
c) $500\sqrt{3}$
d) $675\sqrt{3}$
18000+ Questions – Free SSC Study Material
Question 11: In an equilateral triangle,if h-R=5 cm where h=height of the triangle and R=circumradius then what is the area of the triangle ?
a) $50\sqrt{3}$
b) $100\sqrt{3}$
c) $75\sqrt{3}$
d) $25\sqrt{3}$
Question 12: In an equilateral triangle PQR, PA is the altitude. O is the orthocentre and PO=12 the find the value of PA.
a) 14
b) 20
c) 16
d) 18
Question 13: In an equilateral triangle XYZ, XA is the altitude. O is the orthocentre and XO=8 the find the value of XA.
a) 12
b) 10
c) 16
d) 14
Question 14: In a triangle XYZ, I is the incentre and $\angle XYZ=40$ and $\angle YZX=60$. What is the value of $\angle YIZ $=?
a) 120
b) 130
c) 80
d) 100
Question 15: In a triangle PQR, I is the incentre and $\angle PQR=70$ and $\angle PRQ=40$. What is the value of $\angle QIR $=?
a) 70
b) 135
c) 115
d) 125
Question 16: Find the value of ∠CAB if Internal bisectors of ∠A and ∠B of ΔABC intersect at O and ∠COB = 124°.
a) 36°
b) 16°
c) 96°
d) 68°
Question 17: Find the maximum possible area$(in cm^2)$ of a triangle which can be formed using a thread of length 36 cm.?
a) $45$
b) $39\sqrt{3}$
c) $36\sqrt{3}$
d) $36$
Question 18: If the angles of a triangle PQR are in the ratio 2:3:7, which among the following is a measure of an angle of the triangle PQR?
a) 48°
b) 55°
c) 15°
d) 105°
Question 19: A tangent of length 45 cm is drawn from a point to a circle of diameter 56 cm. Find the length(in cm) of the tangent from the center of the circle?
a) 47
b) 69
c) 53
d) 73
Question 20: $\angle P, \angle Q, \angle R$ are three angles of a triangle. If $\angle P – \angle Q$ = $16^\circ$, $\angle Q – \angle R$ = $28^\circ$, then $\angle P$, $\angle Q$ and $\angle R$ are
a) $76^\circ, 60^\circ, 44^\circ$
b) $80^\circ, 60^\circ, 40^\circ$
c) $80^\circ, 64^\circ, 36^\circ$
d) $76^\circ, 68^\circ, 38^\circ$
1500+ Free SSC Questions & Answers
Answers & Solutions:
1) Answer (A)
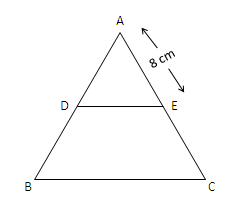
$\dfrac{AD}{DB} = \dfrac{AE}{EC}$
Here, $\dfrac{AD}{DB} = \dfrac{2}{1}$ and AE = 8 cm
⇒ $\dfrac{2}{1} = \dfrac{8}{EC}$
⇒ $EC = 4 cm$
Here, AC = AE+EC = 4+8 = 12 cm
2) Answer (B)
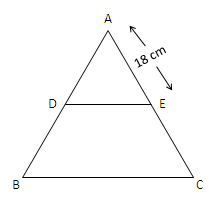
Given, DE is parallel to BC.
Then, $\dfrac{AD}{DB} = \dfrac{AE}{EC}$
Here, $\dfrac{AD}{DB} = \dfrac{3}{1}$
AE= 18 cm
$\dfrac{3}{1} = \dfrac{18}{EC}$
⇒ EC = 6 cm
AC = AE+EC = 6+18 = 24 cm
3) Answer (B)
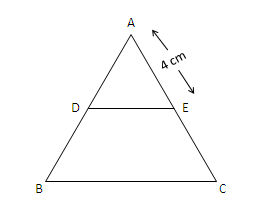
Given, DE is parallel to BC.
Then, $\dfrac{AD}{DB} = \dfrac{AE}{EC}$
Here, $\dfrac{AD}{DB} = \dfrac{2}{5}$
AE= 4 cm
$\dfrac{2}{5} = \dfrac{4}{EC}$
⇒ EC = 10 cm
AC = AE+EC = 4+10 = 14 cm
4) Answer (C)
Given that the coordinates of a right-angled triangle are A (6, 2), B(8, 0) and C (2, -2).
We know that the distance between two points(a, b) &(c, d) is
D = $\sqrt{(a-c)^2+(b-d)^2}$
AB = $2\sqrt{2}$ units; BC = $2\sqrt{10}$; AC = $4\sqrt{2} $
Now, $AB^2 + AC^2 = BC^2$
Therefore, angle A is right angled.
Since it is a right angled triangle, the 2 sides adjacent to the right angle will be altitudes. The third altitude must meet at the vertex at which these 2 sides meet.
Hence, the vertex that contains the right angle is the orthocentre. From the points given, we can clearly see that (6, 2) is the orthocentre. Option C is the right answer,
5) Answer (A)
Given,
AD = 24 cm and ABC is an equilateral triangle
In an equilateral triangle all the angles are equal to 60°
In $\triangle$ADC
=> $tan \angle ACD = \frac{AD}{DC}$
=> $tan 60° = \frac{24}{DC}$
=> DC = $\frac{24}{\sqrt{3}} = 8\sqrt{3}$
=> BC = 2*DC = $16\sqrt{3}$
Area of $\triangle$ ABC = $\frac{\sqrt{3}}{4} * side^2$
= $\frac{\sqrt{3}}{4} * (16\sqrt{3})^2$
= $192\sqrt{3} cm^2$
100+ Free GK Tests for SSC Exams
6) Answer (A)
Given the sides of triangle are 28 m, 45 m and 53 m
Since, $28^2 + 45^2 = 784+2025 = 2809 = 53^2$
=> The given sides are of right angled triangle as,
$c^2 + b^2 = a^2$where a, b, c are the sides of the triangle.
=> Area of triangular field = $\large\frac{1}{2}$ $ \times 28 \times 45= 630 m^2$
=> Cost of sowing seeds = $12 \times 630 = Rs. 7560 rupees/m^2$
7) Answer (C)

Let $\angle Q$=2x and $\angle R$=2y
Sum of angles in a triangle=180
2x+2y+110=180
2x+2y=70
x+y=35
Similarly in the triangle QOR we have $\angle OQR +\angle QRO+ \angle QOR $=180
x+y+$\angle QOR =180^\circ$
35+$\angle QOR =180^\circ$
$\angle QOR =145^\circ$
8) Answer (B)
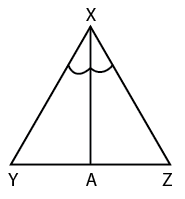
In triangle XYZ we have s=12
(x+y+z)/2 =12
x+y+z=24
12+6+y=24
y=6
Angle bisector divides the opposite side in the ratio of other sides i.e
XY/XZ=YA/AZ
YA/AZ=12/6
YA/AZ=2:1
9) Answer (C)
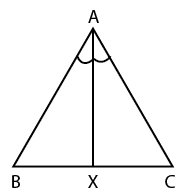
In triangle ABC we have s=9
(a+b+c)/2 =9
a+b+c=18
4+6+b=18
b=8
Angle bisector divides the opposite side in the ratio of other sides i.e
AB/AC=BX/XC
BX/XC=4/8
BX/XC=1:2
10) Answer (D)
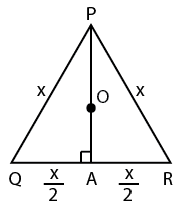
In an equilateral triangle,all the points such as orthocentre,centroid,circumcenter coincide.
Let the triangle be PQR and the circumcentre be O. let median intersect QR at A
Centroid divides median in the ratio 2:1.PA=h,OA=R
OA=15 cm
Therefore (PO:OA)=2:1
PO:15=2:1
PO=30
PA=PO+OP
PA=30+15
PA=45
PA is also the altitude using it side of the triangle can be calculated.
$\sqrt{3}*s/2$=45
s=$30\sqrt{3}$
Area of an equilateral triangle=$\sqrt{3}(s^{2})/4$
=$675\sqrt{3}$
11) Answer (C)

In an equilateral triangle,all the points such as orthocentre,centroid,circumcenter coincide.
Let the triangle be PQR and the circumcentre be O. let median intersect QR at A
Centroid divides median in the ratio 2:1
OA=5 cm
Therefore (PO:OA)=2:1
PO:5=2:1
PO=10
PA=PO+OP
PA=10+5
PA=15
PA is also the altitude using it side of the triangle can be calculated.
$\sqrt{3}*s/2$=15
s=$10\sqrt{3}$
Area of an equilateral triangle=$\sqrt{3}(s^{2})/4$
=$75\sqrt{3}$
12) Answer (D)
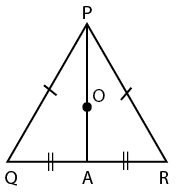
In an equilateral triangle,all the points such as orthocentre,centroid,circumcenter coincide.
So O is also the centroid.
Centroid divides median in the ratio 2:1
Therefore (PO:OA)=2:1
12:OA=2:1
OA=6
PA=PO+PA
PA=12+6
PA=18
15000 Questions – Free SSC Study Material
13) Answer (A)
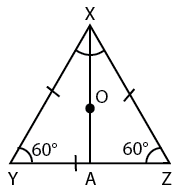
In an equilateral triangle,all the points such as orthocentre,centroid,circumcenter coincide.
So O is also the centroid.
Centroid divides median in the ratio 2:1
Therefore (XO:OA)=2:1
8:OA=2:1
OA=4
XA=XO+OA
XA=8+4
XA=12
14) Answer (B)
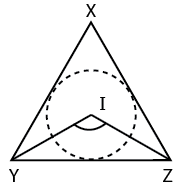
In a triangle XYZ,
$\angle X+\angle Y+\angle Z$=180
Given $\angle Y$=40 $\angle Z $=60
Therefore $\angle X$=180-(40+60)
=80
As I is the incentre we have $\angle YIZ $=90+($\angle X$/2)
=90+40
=130
15) Answer (D)
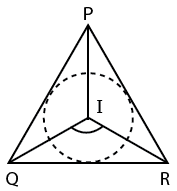
In a triangle PQR,
$\angle P+\angle Q+\angle R$=180
Given $\angle Q$=70 $\angle R $=40
Therefore $\angle P$=180-(40+70)
=70
As I is the incentre we have $\angle QIR $=90+($\angle P$/2)
=90+35
=125
16) Answer (D)

Given that, ∠COB = 124°
To find : $\angle$RPQ = $\theta$ = ?
Solution : Let $\angle$CAB = $2x$ and $\angle$ACB = $2y$
=> $\angle$OBC = $x$ and $\angle$OCB = $y$ [SInce, BO & CO are angle bisectors]
In $\triangle$ABC
=> $\theta$ + $\angle$ABC + $\angle$ACB = 180°
=> $\theta$ = 180° -2$(x+y)$ ———Eq. (1)
In $\triangle$BOC
=> $x + y + 124° = 180°$
=> $x + y = 56°$
Putting value of (x+y) in eq. (1)
=> $\theta$ = $180 – 2*56 = 180-112 = 68°$
17) Answer (C)
The perimeter of the triangle is given as 36 cm.
The triangle of a fixed perimeter will have the maximum possible area when all the sides are of equal length.
So each side should be of length 12 cm for the triangle to have maximum possible area(i.e. Equilateral triangle).
In this case the area will be,
$\frac{\sqrt{3}}{4}\times a^2$
$\frac{\sqrt{3}}{4}\times12\times12$
$=36\sqrt{3}$ $cm^2$
18) Answer (D)
Given, the angles of a triangle PQR are in the ratio 2:3:7
Let the angles of the triangle be 2x,3x and 7x.
Sum of the angles in a triangle = 180°
2x+3x+7x = 180°
12x = 180
x = 15°
The angles are 30°, 45°, 105°
Hence, option D is the correct answer.
19) Answer (C)
Given diameter = 56cm
radius OA = 56/2 = 28 and AB = 45cm
Now, in $\triangle$OAB right angle at A
OB = $\sqrt{(AB)^2 + (OA)^2}$
= $\sqrt{784+2025} = \sqrt{2809}$
= 53 cm
20) Answer (C)
Given $\angle P-\angle Q = 16^\circ \rightarrow (1)$
$\angle Q-\angle R = 28^\circ\rightarrow (2)$
From equation (1), $\angle Q = \angle P-16^\circ$
Substituting $\angle B$ value in equation (2)
$(\angle P-16)-\angle R = 28^\circ$
$\Rightarrow \angle R = \angle P-44^\circ$
We know that $\angle P+\angle Q+\angle R=180^\circ$
Substituting $\angle P,\angle Q,\angle R$ values in above equation
$\angle P+(\angle P-16^\circ)+(\angle P-44^\circ)=180^\circ$
$\Rightarrow 3\angle P=240^\circ$
$\angle P=80^\circ$
Substituting $\angle P$ value in equation (1)
$80^\circ-\angle Q=16^\circ$
$\Rightarrow \angle Q=64^\circ$
Substituting $\angle Q$ in equation (2)
$64^\circ-\angle R = 28^\circ$
$\Rightarrow \angle R = 36^\circ$
$\therefore \angle P=80^\circ, \angle Q=64^\circ, \angle R=36^\circ$
DOWNLOAD APP FOR SSC FREE MOCKS
We hope this Problems on Triangles questions for SSC Exam will be highly useful for your preparation.






