SSC CGL Circle Questions PDF:
Download SSC CGL Circle questions with answers PDF based on previous papers very useful for SSC CGL exams. 25 Very important Circle objective questions for SSC exams.
Download SSC CGL Circle Questions PDF
25 SSC CGL Mocks – Just Rs. 149
Question 1: A copper wire is bent in the form of square with an area of 121 cm 2. If the same wire is bent in the form of a circle, the radius (in cm) of the circle is
a) 7
b) 10
c) 11
d) 14
Question 2: AC and BC are two equal cords of a circle. BA is produced to any point P and CP, when joined cuts the circle at T. Then
a) CT : TP = AB : CA
b) CT : TP = CA : AB
c) CT : CB = CA : CP
d) CT : CB = CP : CA
Question 3: The diagonals AC and BD of a cyclic quadrilateral ABCD intersect each other at the point P. Then, it is always true that
a) AP . CP = BP . DP
b) AP . BP = CP . DP
c) AP . CD = AB . CP
d) BP . AB = CD . CP
Question 4: A, B, C, D are four points on a circle. AC and BD intersect at a point such that $\angle{BEC} = 130^o$ and $\angle{ECD} = 20^o$. Then, $\angle{BAC}$ is
a) 90 $^{\circ}$
b) 100 $^{\circ}$
c) 110 $^{\circ}$
d) 120 $^{\circ}$
Question 5: ABCD is a cyclic trapezium with AB || DC and AB = diameter of the circle. If angleCAB = $30^{\circ}$, then angleADC is
a) $60^{\circ}$
b) $120^{\circ}$
c) $150^{\circ}$
d) $30^{\circ}$
SSC CGL Previous Papers Download PDF
Question 6: AB is the chord of a circle with centre O and DOC is a line segement originating from a point D on the circle and intersecting AB produced at C such that BC = OD. If $\angle$BCD =$20^{\circ}$, then $\angle$AOD =?
a) $20^{\circ}$
b) $30^{\circ}$
c) $40^{\circ}$
d) $60^{\circ}$
Question 7: A square ABCD is inscribed in a circle of unit radius. Semicircles are described on each side of a diameter. The area of the region bounded by the four semicircles and the circle is
a) 1 sq. unit
b) 2 sq. unit
c) 1.5 sq. unit
d) 2.5 sq. unit
Question 8: Two circles touch each other internally. Their radii are 2 cm and 3 cm. The biggest chord of the greater circle which is outside the inner circle is if length
a) $2\sqrt{2}$ cm
b) $3\sqrt{2}$ cm
c) $2\sqrt{3}$ cm
d) $4\sqrt{2}$ cm
Question 9: What is the length of the arc if it subtends 48° at the center of a circle with radius r = 7 cm.
a) 7.28 cm
b) 8.16 cm
c) 5.867 cm
d) 6.48 cm
Question 10: What is the length of the chord of a circle of radius 5 cm, if the perpendicular distance between centre and chord is 4 cm.
a) 9 cm
b) 7 cm
c) 6 cm
d) 8 cm
18000+ Questions – Free SSC Study Material
Question 11: A triangle has sides 5 cm, 12 cm and 13 cm. What is the approximate area of the circumcircle of this triangle?
a) 120 $cm^2$
b) 128 $cm^2$
c) 132 $cm^2$
d) 136 $cm^2$
Question 12: If the perpendicular distance between the centre of a circle and a chord of length 8m is 3m, what is the radius of the circle?
a) 7m
b) 4m
c) 5m
d) 3m
Question 13: What is the area of the sector subtending 36° at the centre of a circle with a radius of 7cm ?
a) 16.8 sq.cm
b) 15.4 sq.cm
c) 17.2 sq.cm
d) 18.6 sq.cm
Question 14: A certain length of a wire was bent to form the shape of a square, the area of the. square thus formed is 81 sq-cm. Now, the wire is rebent into a semicircular shape, calculate the area of the semicircle formed ( in sq-cm )
a) 88 sq-cm
b) 22 sq-cm
c) 154 sq-cm
d) 77 sq-cm
Question 15: A straight copper wire has been bent to form an equilateral triangle of area $121\sqrt{3}\text{ cm}$ . Find the Area, if the wire is bent in the form of a circle
a) 330.5 sq-cm
b) 350.5 sq-cm
c) 346.5 sq-cm
d) 364.5 sq-cm
Question 16: There are two concentric circle with radii 5 cm and 13 cm. What is the length of the chord of the outer circle which touches the inner circle?
a) 12 cm
b) 18 cm
c) 24 cm
d) 30 cm
Question 17: The area of a circle is 50 $cm^2$. What is the approximate perimeter of the circle?
a) 20 cm
b) 25 cm
c) 30 cm
d) 35 cm
Question 18: A thread of length 1256 cm is used to form a circle. What will be the diameter of the circle formed?
a) 200 cm
b) 500 cm
c) 300 cm
d) 400 cm
Question 19: Two circles externally touch each other. The sum of their areas is $520\pi$ sq-cm and the distance between their center is $28$ cm. The radius of the smaller circle is
a) $4$cm
b) $8$cm
c) $10$cm
d) $6$cm
Question 20: A circle is circumscribed around an equilateral triangle of side 3 cm. What is the area of the circle (in $cm^2$)?
a) $\sqrt3 \pi$
b) $3 \pi$
c) $3\sqrt3 \pi$
d) $9\pi$
100+ Free GK Tests for SSC Exams
Question 21: If the length of the side of a square is equal to the diameter of a circle, what is the ratio of area of square to that of the circle?
a) $2:\pi$
b) $\pi : 4$
c) $4:\pi$
d) $1:\pi$
Question 22: The distance between the centres of the two circles of radii r1, and r2 is d. They will touch each other internally if
a) $d = r_1$ or $r_2$
b) $d = r_1 + r_2$
c) $d = r_1 – r_2$
d) $d = \sqrt{ r_1 r_2}$
Question 23: ΔABC is a right angled triangle with AB = 6 cm, AC = 8 cm, ∠BAC = 90′. Then the radius of the incircle is
a) 4 cm.
b) 2 cm.
c) 6 cm.
d) 3 cm.
Question 24: O is the circumcentre of the triangle ABC and ∠BAC = 85°, ∠BCA = 75°, then the value of ∠OAC is
a) 55°
b) 150°
c) 20°
d) 70°
Question 25: Two chords of length a unit and b unit of a circle make angles 60° and 90° at the centre of a circle respectively, then the correct relation is
a) b = 3/2a
b) b = √2a
c) b = 2a
d) b = √3a
1500+ Free SSC Questions & Answers
Answers & Solutions:
1) Answer (A)
Area of square is $121 = (l)^2$ (where $l$ is length of side)
So length will be = 11
Total length of wire will be = 44
So when it forms a circle, perimeter will be equal to 44
Hence $2\pi r$ = 44
or $r$ = 7
2) Answer (C)
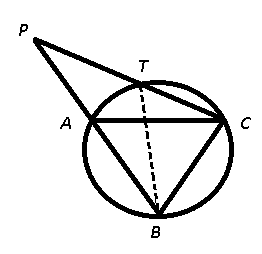
It is given that AC = BC, also $\triangle$ PTB and $\triangle$ PAC are similar, we have :
$\frac{CA}{CP}=\frac{BT}{BP}$ —————-(i)
Also, we have $\angle$ PBC = $\angle$ BTC ($\because$ $\angle$ PBC = $\angle$ BAC = $\angle$ BTC) and $\angle$ PCB = $\angle$ BCT
=> $\triangle$ PBC $\sim$ $\triangle$ BTC
Thus, $\frac{CB}{BP}=\frac{CT}{BT}$
=> $\frac{BT}{BP}=\frac{CT}{CB}$ ————–(ii)
From equations (i) and (ii), we get :
$\frac{CA}{CP}=\frac{CT}{CB}$
=> Ans – (C)
3) Answer (A)
As we know that a cyclic quadrilateral can be inscribed into a circle, Hence in triangle APB and in triangle CPD.
$\angle PAB = \angle PDC$ (same sector angles)
$\angle PCD = \angle PBA$ (same sector angles)
Hence third angle will also be equal and they will be similar triangles.
So $\frac{AP}{PD} = \frac{BP}{PC}$
4) Answer (C)
Angle ABD will be equal to angle ACD = $20^o$ (same sector angles)
Angle BEC = $130^o$ so angle AED = $130^o$ (concurrent angles)
Now angle BEA will be $\frac{360-130-130}{2} = 50^o$
So angle EDC will be $180-(50+20) = 110^o$
5) Answer (B)
let angle CDA = x
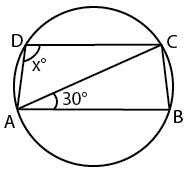
since AB is parallel to CD, angle ACD=30 and angle CAD=30
in triangle ACD,
sum of all three angles = 180
30 + 30 + x = 180
x = 120
so the answer is option B.
6) Answer (D)
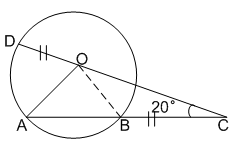
It is given that OD = BC and OD = OB (radii of circle)
=> OB = BC
=> $\angle$ BCO = $\angle$ BOC = $20^\circ$ (Angle opposite to equal sides are equal)
Then, $\angle$ OBC = $180^\circ-(\angle BCO +\angle BOC)$
=> $\angle$ OBC = $180^\circ-20^\circ-20^\circ=140^\circ$
Also, $\angle$ OBA + $\angle$ OBC = $180^\circ$ (Linear pair)
=> $\angle$ OBA = $\angle$ OAB = $180^\circ-140^\circ=40^\circ$
Now, $\angle$ AOB = $180^\circ-(\angle OAB +\angle OBA)$
=> $\angle$ AOB = $180^\circ-40^\circ-40^\circ=100^\circ$
$\therefore$ $\angle$ AOD = $180^\circ-(\angle AOB +\angle BOC)$ (Linear pair)
= $180^\circ-100^\circ-20^\circ=60^\circ$
=> Ans – (D)
7) Answer (B)
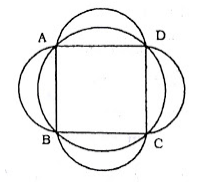
Radius of the circle = 1 unit, => Diameter = BD = 2 units
Thus, side of square = AB = $\sqrt2$ units
Radius of a semi-circle = $\frac{AB}{2}=\frac{\sqrt2}{2}=\frac{1}{\sqrt2}$
=> Area of 4 semi-circles = $2\pi r^2$
= $2\pi (\frac{1}{\sqrt2})^2=\pi$ sq. units ————(i)
Area bounded by region = Area of circle – Area of square
= $\pi(1)^2-(\sqrt2)^2=(\pi-2)$ sq. units —————(ii)
$\therefore$ Required area bounded by 4 semi circles = (i) – (ii)
= $\pi – (\pi-2) = 2$ sq. units
=> Ans – (B)
8) Answer (D)

The biggest chord lying outside the inner circle must be tangential to it.
By pytagoras theorem,
$x = \sqrt{3^2 – 1^2} = \sqrt{9-1} = \sqrt{8} = 2 \sqrt{2}$
The length of the chord is 2x = $4 \sqrt{2}$
Hence Option D is the correct answer.
9) Answer (C)
Length of the arc = (angle subtended by the arc/360)*circumference of the circle = $\frac{48}{360}*2* \pi * 7$ = 5.867 cm.
10) Answer (C)
The information given in the question can be represented as below
1/2(length of the chord) = $\sqrt(5^2 – 4^2)$
==> Length of the chord = 2*3 = 6cm
11) Answer (C)
The given triangle is a right angled triangle.
The length of the hypotenuse is 13 cm.
In a right angled triangle the length of the circumradius is half the length of the hypotenuse.
So, circumradius = 13/2 = 6.5 cm
Area of the circumcircle = $3.14*(6.5)^2=132.665$ $cm^2$
12) Answer (C)
Here, the radius of the circle is the hypotenuse of the triangle with 4m,3m as its base and height.
Radius = $\sqrt{4^{2}+3^{2}}$
Radius =$5 m$
13) Answer (B)
Area of sector of a circle = $\frac{x}{360}*\pi *r^{2}$
Where x is the angle subtended at the centre and r is the radius of the circle
Area =$\frac{36}{360}*\pi *7^{2}$ = 15.4 sq.cm
14) Answer (D)
Area of the square form is 81 sq-cm . Hence , the side of the square would be 9 cm .
Length of the wire is (9 x 4) cm = 36 cm . Let $r$ be the radius of the semicircle thus formed .
When the wire is bent into semicircular shape , $\pi r + 2r = 36$
$\implies r = \frac{36}{\frac{22}{7}+2} = \frac{36}{\frac{36}{7}} = 7$ cm
Therefore , Area of the semicircle = $\frac{\frac{22}{7}\times7\times7}{2}$ = $77$ sq-cm
Hence , the correct Option is D
15) Answer (C)
Area of the triangle , $A$ = $\frac{\sqrt{3}}{4}a^2$ = $121\sqrt{3}$
$\implies a = 22\text{ cm}$
Length of wire, $L$ = $(3\times a)\text{ cm}$ = $66\text{ cm}$
Let radius of the circle be $r$
By using the relation,
$2\pi r = 66$
$\implies r = \frac{66\times 7}{2\times 22} = 10.5 \text{ cm}$
$\implies \text{ Area} = \pi \times 10.5^2 = 346.5 \text{ cm}^2$
Hence , the correct Option is C
16) Answer (C)
Let AB be the chord described as shown in the figure.

OA is the radius of the bigger circle and OC is the radius of the smaller circle.
We can observe that the triangle OAC is a right triangle.
Applying Pythagoras theorem we get,
$AC^2=13^2-5^2$
$=>AC=12$ cm
The length of the chord is twice the length of AC. So we get,
AB = 2*AC = 2*12 = 24 cm
17) Answer (B)
Let the radius of the circle be ‘r’
It is given that $\pi r^2=50$
$=>r^2=\frac{50}{3.14}$
$=>r^2\approx 16$
$r\approx 4$ cm
The perimeter will be
$=2*\pi*r$
$=2*3.14*4$
$\approx 25$ cm
18) Answer (D)
Let the radius of the circle formed be ‘r’
The length of the thread will be the circumference of the circle.
So we get,
$2\pi r=1256$
$=>2*3.14*r=1256$
$r=200$ cm
Thus the diameter will be 400 cm.
19) Answer (D)
Let the radius of the circles touching each other be $a$ cm and $b$ cm .
Then , $a$ + $b$ = $28$
$\implies b$ = $28 – a$
$\implies \pi a^2+ \pi b^2$ = $520\pi$
$\implies a^2+(28-a)^2$ = $520$
$\implies 2a^2 – 56a + 784 = 520$
$\implies 2a^2 – 56a + 264 = 0$
$\implies 2( a – 6 )( a – 22 ) = 0$
The radius of the circles can be $22$cm or $6$ cm
Therefore , the radius of the smaller circle is $6$ cm
Hence, correct option is D
20) Answer (B)
The circle is the circumcircle of the equilateral triangle.
Circumradius = $\frac{2}{3}*\frac{\sqrt3}{2}*3=\sqrt3$ cm
Area of the circle = $\pi*(\sqrt3)^2=3 \pi$ $cm^2$
Hence Option B.
21) Answer (C)
Let the length of the side be ‘l’
Area of square = $l^{2}$
Area of the circle = $\pi\times\frac{l^{2}}{4}$
Required ratio = $l^{2}$:$\pi\times\frac{l^{2}}{4}$
Required ratio =$4:\pi$
22) Answer (C)
The distance between centres of two circles = d
Radius of both circles = $r_1$ and $r_2$
For the circles to touch each other internally,
Here, AC = $r_1$ and BC = $r_2$
Distance between their centres = AB = d
Now, clearly AB = AC – BC
=> d = $r_1-r_2$
23) Answer (B)
NOTE :- Area of triangle = (semi perimeter) * (inradius)
AB = 6 cm , AC = 8 cm and $\angle$BAC = 90°
From $\triangle$ABC,
BC = $\sqrt{(AB)^2+(AC^2)}$
= $\sqrt{6^2+8^2} = \sqrt{36+64}$
= 10 cm
Semi perimeter of $\triangle$ABC = s
= $\frac{6+8+10}{2}$ = 12 cm
Area of $\triangle$ABC = $\frac{1}{2}$*AB*AC
= $\frac{1}{2}$*6*8 = 24 $cm^2$
=> Inradius = $\frac{\triangle}{s}$ = $\frac{24}{12}$
= 2 cm
24) Answer (D)
$\angle$BAC = 85°
$\angle$BCA = 75°
=> $\angle$ABC = 180°-(85°+75°) = 20°
Angle subtended by an arc at the centre is twice the angle subtended by it at any point on the circle.
=> $\angle$AOC = 2$\angle$ABC
=> $\angle$AOC = 40°
In $\triangle$OAC, OA = OC = radii
=> $\angle$OAC = $\angle$OCA
=> 2$\angle$OAC = 180°-40° = 140°
=> $\angle$OAC = $\frac{140^{\circ}}{2}$ = 70°
25) Answer (B)
Length of chord CD = $a$ and AB = $b$
Let radius of the circle be $r$
In $\triangle$OAB, by using Pythagoras theorem
=> $r^2 + r^2 = b^2$
=> $2r^2 = b^2$
=> $r = \frac{b}{\sqrt{2}}$ ——Eqn(1)
Now, in $\triangle$COD, OC = OD = radii
=> $\angle$OCD = $\angle$ODC = $\angle$COD = 60°
=> OCD is equilateral triangle
=> $a = r$ ———Eqn(2)
From eqns(1) & (2), we get :
$a = \frac{b}{\sqrt{2}}$
=> $b = \sqrt{2}a$











