Set Theory Questions for CAT Set-2 PDF
Download important Set Theory Set-2 Questions for CAT PDF based on previously asked questions in CAT exam. Practice Set Theory Set-2 Questions PDF for CAT exam.
Download Set Theory Questions for CAT Set-2 PDF
CAT Test series at just Rs. 299. Enroll here
Download CAT Quant Questions PDF
Take 3 Free Mock Tests for CAT
Question 1: If A = {$6^{2n} -35n – 1$}, where $n$ = 1,2,3,… and B = {35($n$-1)}, where $n$ = 1,2,3,… then which of the following is true?
a) Every member of A is in B and at least one member of B is not in A
b) Neither every member of A is in B nor every member of B is in A
c) Every member of B is in A.
d) At least one member of A is not in B
Question 2: For two sets A and B, let AΔB denote the set of elements which belong to A or B but not both. If P = {1,2,3,4}, Q = {2,3,5,6,}, R = {1,3,7,8,9}, S = {2,4,9,10}, then the number of elements in (PΔQ)Δ(RΔS) is
Question 3: If among 200 students, 105 like pizza and 134 like burger, then the number of students who like only burger can possibly be
a) 23
b) 26
c) 96
d) 93
Question 4: Each of 74 students in a class studies at least one of the three subjects H, E and P. Ten students study all three subjects, while twenty study H and E, but not P. Every student who studies P also studies H or E or both. If the number of students studying H equals that studying E, then the number of students studying H is
Question 5: In the final semester, an engineering college offers three elective courses and one mandatory course. A student has to register for exactly three courses: two electives and the mandatory course. The registration in three of the four courses is: 45, 55 and 70. What will be the number of students in the elective with the lowest registration?
a) 35
b) 40
c) 42
d) 45
e) Either B or D
Take 3 free mock tests for CAT
Download CAT Quant Questions PDF
Question 6: 70% of the students who joined XCRI last year play football, 75% play cricket, 80% play basketball and 85% play carrom. The minimum percentage of students who play all four games is:
a) 5%
b) 10%
c) 15%
d) 20%
e) None of the above
Question 7: In a class of 60, along with English as a common subject, students can opt to major in Mathematics, Physics, Biology or a combination of any two. 6 students major in both Mathematics and Physics, 15 major in both Physics and Biology, but no one majors in both Mathematics and Biology. In an English test, the average mark scored by students majoring in Mathematics is 45 and that of students majoring in Biology is 60. However, the combined average mark in English, of students of these two majors, is 50. What is the maximum possible number of students who major ONLY in Physics?
a) 30
b) 25
c) 20
d) 15
e) None of the above
Question 8: In a certain village, 22% of the families own agricultural land, 18% own a mobile phone and 1600 families own both agricultural land and a mobile phone. If 68% of the families neither own agricultural land nor a mobile phone, then the total number of families living in the village is:
a) 20000
b) 10000
c) 8000
d) 5000
Question 9: There are 240 second year students in a B – School. The Finance area offers 3 electives in the second year. These are Financial Derivatives, Behavioural Finance, and Security Analysis. Four students have taken all the three electives, and 48 students have taken Financial Derivatives. There are twice as many students who study Financial Derivatives and Security Analysis but not Behavioural Finance, as those who study both Financial Derivatives and Behavioural Finance but not Security Analysis, and 4 times as many who study all the three. 124 students study Security Analysis. There are 59 students who could not muster courage to take up any of these subjects. The group of students who study both Financial Derivatives and Security Analysis but not Behavioural Finance, is exactly the same as the group made up of students who study both Behavioural Finance and Security Analysis. How many students study Behavioural Finance only?
a) 29
b) 30
c) 32
d) 35
e) None of the above
Question 10: There are 240 second year students in a B – School. The Finance area offers 3 electives in the second year. These are Financial Derivatives, Behavioural Finance, and Security Analysis. Four students have taken all the three electives, and 48 students have taken Financial Derivatives. There are twice as many students who study Financial Derivatives and Security Analysis but not Behavioural Finance, as those who study both Financial Derivatives and Behavioural Finance but not Security Analysis, and 4 times as many who study all the three. 124 students study Security Analysis. There are 59 students who could not muster courage to take up any of these subjects. The group of students who study both Financial Derivatives and Security Analysis but not Behavioural Finance, is exactly the same as the group made up of students who study both Behavioural Finance and Security Analysis. How many students study Behavioural Finance only?
a) 29
b) 30
c) 32
d) 35
e) None of the above
Download CAT Quant Questions PDF
CAT Test series at just Rs. 299. Enroll here
Answers & Solutions:
1) Answer (A)
If we carefully observe set A, then we find that $6^{2n} -35n – 1$ is divisible by 35. So, set A contains multiples of 35. However, not all the multiples of 35 are there in set A, for different values of $n$.
For $n = 1$, the value is 0, for $n = 2$, the value is 1225 which is the 35th multiple of 3.
If we observe set B, it consists of all the multiples of 35 including 0.
So, we can say that every member of set A will be in B while every member of set B will not necessarily be in set A.
Hence, option A is the correct answer.
2) Answer: 7
P = {1,2,3,4} and Q = {2,3,5,6,}
PΔQ = {1, 4, 5, 6}
R = {1,3,7,8,9} and S = {2,4,9,10}
RΔS = {1, 2, 3, 4, 7, 8, 10}
(PΔQ)Δ(RΔS) = {2, 3, 5, 6, 7, 8, 10}
Thus, there are 7 elements in (PΔQ)Δ(RΔS) .
hence, 7 is the correct answer.
3) Answer (D)
It has been given that among 200 students, 105 like pizza and 134 like burger.
The question asks us to find out the number of students who can be liking only burgers among the given values.
The least number of students who like only burger will be obtained when everyone who likes pizza likes burger too.
In this case, 105 students will like pizza and burger and 134-105 = 29 students will like only burger. Therefore, the number of students who like only burger cannot be less than 29.
The maximum number of students who like only burger will be obtained when we try to separate the 2 sets as much as possible.
There are 200 students in total. 105 of them like pizza. Therefore, the remaining 95 students can like only burger and 134-95 = 39 students can like both pizza and burger. As we can see, the number of students who like burger cannot exceed 95.
The number of students who like only burger should lie between 29 and 95 (both the values are included).
93 is the only value among the given options that satisfies this condition and hence, option D is the right answer.
4) Answer: 52
Let us draw a Venn diagram using the information present in the question.
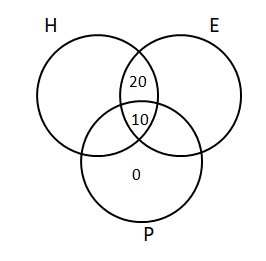
It is given that the number of students studying H equals that studying E.
Let ‘x’ be the total number of students who studied H, and H and P but mot E.We can also say that the same will be the number of students who studied E, and E and P but not H.Therefore,
x + 20 + 10 + x = 74
x = 22
Hence, the number of students studying H = 22 + 10+ 20 = 52
5) Answer (E)
The number of candidates registered for 3 of the 4 courses is 45, 55, and 70.
There are 2 cases.
70 can be the total number of students registered in an elective or the mandatory course.
Case (i):
70 students have registered in an elective.
Each student will choose 2 elective.
=> Total number of electives chosen = 2* total number of students.
45+55+70 = 2*number of students.
Number of students = 170/2 = 85.
In this case, at least 45 students would have selected an elective.
Case (ii):
70 students have registered in the mandatory class.
=> 45+55+x = 2*70
=> x =40.
As we can see, the number of students registered in an elective can be 40 or 45. Therefore, option E is the right answer.
Free CAT Practice – Study Material
Download CAT Quant Formulas PDF
6) Answer (B)
Let ‘100x’ be the number of students who joined XCRI last year.
Let ‘a’, ‘b’, ‘c’ and d be the number of students who play 1 game, 2 games, 3 games and 4 games respectively.
Therefore,
a+b+c+d = 100x … (1)
a+2b+3c+4d = 70x+75x+80x+85x
a+2b+3c+4d = 310x … (2)
By equation (2) – (1)
b+2c+3d = 210x
We have to minimize ‘d’ for that we have to maximize c. But c $\leq$ 100x
At c$_{max}$ = 90x, d$_{min}$ = 10x
Therefore, we can say that the minimum percentage of students who play all four games = 10%.
7) Answer (D)
Let us note down the information given:
No person can major in all 3 subjects. 6 students major in both Mathematics and Physics, 15 major in both Physics and Biology, but no one majors in both Mathematics and Biology. There are 60 students in total.

It has been given that average marks scored by students majoring in Maths in English is 45.
Average marks scored by students majoring in Biology in English is 60.
But the combined average marks scored by students majoring in Maths and Biology in English is 50.
=> $\dfrac{45*(a+6) + 60*(c+15)}{a+6+c+15} = 50$
$45a+270+60c+900 = 50a+50c+1050$
$5a=10c+120$
$a=2c+24$
To maximize b, we have to minimize ‘a’ and ‘c’. The least value that ‘c’ can take is 0.
The corresponding value of a is 24.
24+6+b+15 = 60
=> b = 15.
Therefore, the maximum number of students who could have majored only in physics is 15. Therefore,option D is the right answer.
8) Answer (A)
22% of the families own agricultural land, 18% own a mobile phone, 1600 families own both and 68% families own none.
P(A $\cup$ B) = P(A) + P(B) – P(A $\cap$ B)
32 = 22 + 18 – x
x=8. Hence, there will be 8% families who own both.
8% =1600 (Given in question)
Total families in a village =>100% = 20000
9) Answer (A)

Given : $e = 4$
$FD = 48$, => $a + b + d + e = 48$
$d = 2b$ and $d = 4e$
$SA = 124$, => $d + e + f + g = 124$
$d = e + f$ and $h = 59$
To find : $c = ?$
Solution : $d = 4e = 4 \times 4 = 16$
=> $b = \frac{d}{2} = \frac{16}{2} = 8$
=> $f = d – e = 16 – 4 = 12$
=> $a = 48 – b – d – e = 48 – 8 – 16 – 4 = 20$
=> $g = 124 – d – e – f = 124 – 16 – 4 – 12 = 92$
Now, we know that, $a + b + c + d + e + f + g + h = 240$
=> $20 + 8 + c + 16 + 4 + 12 + 92 + 59 = 240$
=> $c + 211 = 240$
=> $c = 240 – 211 = 29$
10) Answer (A)

Given : $e = 4$
$FD = 48$, => $a + b + d + e = 48$
$d = 2b$ and $d = 4e$
$SA = 124$, => $d + e + f + g = 124$
$d = e + f$ and $h = 59$
To find : $c = ?$
Solution : $d = 4e = 4 \times 4 = 16$
=> $b = \frac{d}{2} = \frac{16}{2} = 8$
=> $f = d – e = 16 – 4 = 12$
=> $a = 48 – b – d – e = 48 – 8 – 16 – 4 = 20$
=> $g = 124 – d – e – f = 124 – 16 – 4 – 12 = 92$
Now, we know that, $a + b + c + d + e + f + g + h = 240$
=> $20 + 8 + c + 16 + 4 + 12 + 92 + 59 = 240$
=> $c + 211 = 240$
=> $c = 240 – 211 = 29$
Download CAT Previous Papers PDF
Download Free CAT Preparation App
We hope this Set Theory Set-2 Questions PDF for CAT with Solutions will be helpful to you.





![CAT Averages Questions PDF [Important Questions] CAT AVERAGES Questions PDF](https://cracku.in/blog/wp-content/uploads/2022/07/CAT-AVERAGES-Questions-PDF-218x150.png)