RRB NTPC Mensuration Questions PDF
Download RRB NTPC Mensuration Questions and Answers PDF. Top 20 RRB NTPC Maths questions based on asked questions in previous exam papers very important for the Railway NTPC exam.
Download RRB NTPC Mensuration Questions PDF
Take a free mock test for RRB NTPC
Download RRB NTPC Previous Papers PDF
Question 1: In triangle ABC, AB = 30 cm, BC = 40 cm and CA = 50 cm. Points P and Q are on side AC such that AP = BQ. Similarly, points R and S are on side CB such that CR = BS, and points T and U are on side AB such that AU = BT. If AP=BQ=CR=BS=AU=BT= 10 cm, then find the area(in cm$^2$) of hexagon PQRSTU.
Question 2: A circle is given by $x^2+ y^2 = a^2$. Tangents are drawn to the circle. Find the area of the shaded region.
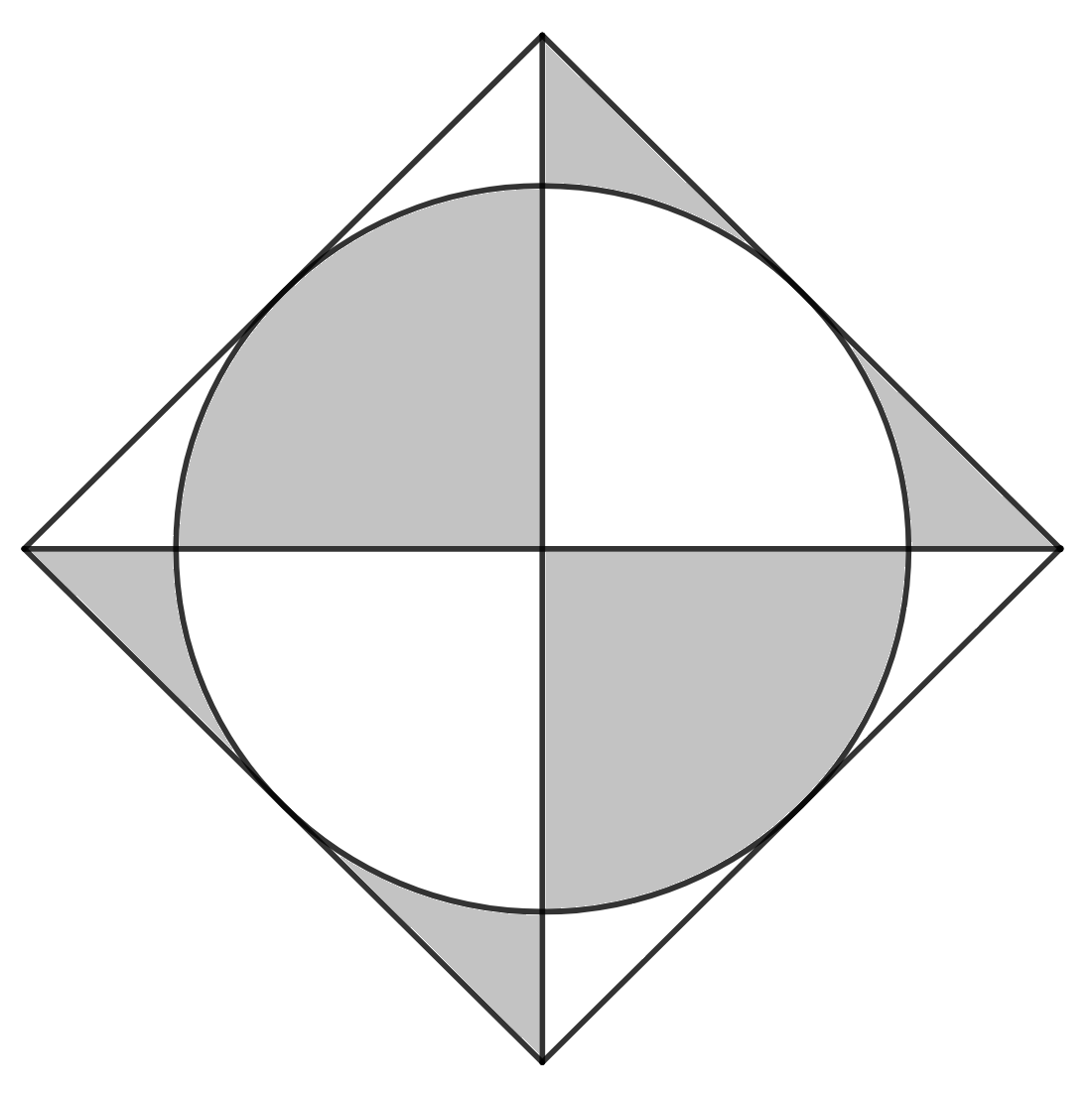
a) $2a^2$ units
b) $4\sqrt{2}a^2$ units
c) $a^2$ units
d) $2\sqrt{2}a^2$ units
Question 3: A right circular cone of the radius of radius 12 cm is inverted, such that base of the cone is open to surroundings. The inverted cone is partly filled with milk which leaks from a hole at the tip at the rate of 2*Pi $cm^3$/ hour. At a particular instance, the surface area of milk exposed to surrounding is 81*Pi $cm^2$, when the milk is at 5 cm from the broader end of the cone. How much time will it take for the cone to empty completely from this instant?
a) 202.5 hours
b) 67*Pi hours
c) 103 hours
d) 32*Pi hours
RRB NTPC Previous Papers [Download PDF]
Question 4: There is a square foil of side 42 cm. Four equal small squares each of side ‘a’ cm are cut off from each of the corners of the square foil and the left over foil is folded to form an open cuboid. What is the largest possible volume of such a cuboid? (in cc.)
Question 5: Two spheres of equal radii are fitted inside a cube of side 8 cm in such a way that the spheres are having maximum radius. Find the volume of the sphere.
a) $\frac{4\pi [8\sqrt{3}]^3}{3(2+2\sqrt{3})^3}$
b) $\frac{4\pi [12\sqrt{3}]^3}{3(2+2\sqrt{3})^3}$
c) $\frac{2048\pi }{3(2+\sqrt{2})^3}$
d) $\frac{1024\pi }{3(2+\sqrt{2})^3}$
Question 6: In order to form a cube, whose each side is 4cm, find the minimum number of cuboids of dimensions 3cm*2cm*1cm that have to be melted.
a) 10
b) 11
c) 12
d) None of these
Question 7: A square sheet of side 10m is taken and 4 squares of side 2 m each are cut from the 4 corners of the sheet.The remaining part of the sheet is folded to form a cuboid with an open end.Find the volume of the cuboid so formed?
a) 60
b) 72
c) 80
d) 128
Question 8: A circle contains 2 perpendicular chords AB and CD. The length of chord AB is 6 cm and that of chord CD is 12 cm. C is closer to A and B than D. If it is known that chord CD passes through O, the centre of the circle, what is the area of the polygon AOBD?
a) 9 $ cm^2$
b) 18 $cm^2$
c) 36 $cm^2$
d) 27 $cm^2$
Question 9: Each side of the rhombus ABCD is 15 cm. One of the internal angle is three times the adjacent angle. What is the product of diagonals?
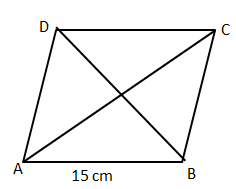
a) $\frac{125}{\sqrt{2}}$
b) $\frac{450}{\sqrt{2}}$
c) $\frac{450}{\sqrt{3}}$
d) $\frac{225}{\sqrt{3}}$
Question 10: A rectangle has sides measuring 24 cm and 27 cm. Two circles A and B are inside the rectangle. Circle A touches three sides of the rectangle while circle B touches two perpendicular sides of the rectangle and also touches circle A externally. What will be the approximate area of rectangle leaving the two circles?
a) 156.92 $cm^2$
b) 159.37 $cm^2$
c) 174.48 $cm^2$
d) 167.14 $cm^2$
18000+ Questions – Free SSC Study Material
Download General Science Notes PDF
Question 11: From a solid cube of side 8cm, a portion is cut out such that the cutting plane touches the midpoints of three adjacent sides of the cube. Find the surface area of the cut out portion.
a) $10 + 5\sqrt{2}$
b) $24+ 8\sqrt{3}$
c) $32 + 4\sqrt{3}$
d) $16+ 5\sqrt{2}$
Question 12: If the diagonals of a rhombus of side 15 cm are in the ratio 3:4, find the area of the rhombus.
a) 54 sq. cm.
b) 108 sq. cm.
c) 144 sq. cm.
d) 200 sq. cm.
e) None of the above
Question 13: A ladder of 7.6 m long is standing against a wall and the difference between the wall and the base of the a ladder is 6.4 m. If the top of the ladder now slips by 1.2m, then the foot of the ladder shifts by approximately:
a) 0.4 m
b) 0.6 m
c) 0.8 m
d) 1.2 m
Question 14: If a right circular cylinder of height 14 $cm$ is inscribed in a sphere of radius 8 $cm$, then the volume of the cylinder is:
a) 110 $cm^3$
b) 220 $cm^3$
c) 440 $cm^3$
d) 660 $cm^3$
Question 15: A right circular cylinder has a radius of 6 and a height of 24. A rectangular solid with a square base and a height of 20, is placed in the cylinder such that each of the corners of the solid is tangent to the cylinder wall. If water is then poured into the cylinder such that it reaches the rim, the volume of water is:
a) 288(π – 5)
b) 288(2π – 3)
c) 288(3π – 5)
d) None of the above
Question 16: A rectangular piece of paper is 22 cm. long and 10 cm. wide. A cylinder is formed by rolling the paper along its length. Find the volume of the cylinder.
a) 175 cm3
b) 180 cm3
c) 185 cm3
d) None of the above
Daily Free RRB Online Tests for RRB Exams
Question 17: In a triangle ABC, if AB =7cm and BC = 8cm, for what value of AC is the area of the triangle maximum?
a) 15
b) $\sqrt{123}$
c) $\sqrt{113}$
d) 9
Question 18: PQRS is a square. Point A is on the side PQ such that AP = 4.5 cm. If it is known that the area of triangle AQR is 50 $cm^2$, what is the area of the square PQRS?
a) 141.75 $cm^2$
b) 148.50 $cm^2$
c) 156.25 $cm^2$
d) 160.50 $cm^2$
Question 19: $6$cm and $2\sqrt{11}$cm are the lengths of the side and the shorter diagonal of a Rhombus respectively. If the Rhombus is rotated on its longer diagonal to form a solid, What is the volume of the solid?
a) $\frac{105\pi}{3}$
b) $\frac{55\pi}{3}$
c) $\frac{110\pi}{3}$
d) $\frac{115\pi}{3}$
Question 20: A trapezium PQRS has PQ || RS. PQ = 4cm and RS 6cm. The diagonals of the trapezium meets at point O and the area of triangle POQ = 24 $cm^2$. What is the area of the trapezium PQRS?
a) 100 $cm^2$
b) 250 $cm^2$
c) 150 $cm^2$
d) 200 $cm^2$
Download Current Affairs Questions & Answers PDF
Answers & Solutions:
1) Answer: 480
We can see that $AB^2+BC^2=30^2+40^2=2500=50^2=AC^2$. Hence, we can say that $\triangle$ ABC is a right angled triangle. Drawing the figure according to the information given in the problem statement:
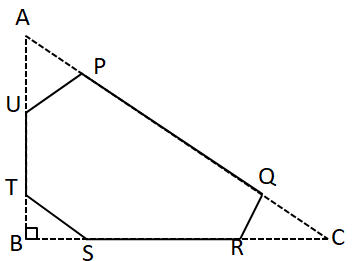
We have to find out the area of hexagon PQRSTU. We can find out the area of hexagon by subtracting area of triangles APU, BTC and QRC from the area of triangle ABC.
Area of triangle ABC = $\dfrac{1}{2}\times AB*BC$ = $\dfrac{1}{2}\times 30*40$ = 600 cm$^2$
Area of triangle APU = $\dfrac{1}{2}\times AU*AP$*$sin(UAP)$ {We know that $sin(UAP)=sin(BAC)=\dfrac{BA}{AC}=\dfrac{40}{50}$=$\dfrac{4}{5}$
$\Rightarrow$ Area of triangle APU = $\dfrac{1}{2}\times 10*10*\dfrac{4}{5}$ = 40 cm$^2$
Similarly, area of triangle QCR = $\dfrac{1}{2}\times CQ*CR*sinQCR$ = $\dfrac{1}{2}\times 10*10*\dfrac{3}{5}$ = 30 cm$^2$
Area of right-angled $\triangle$ SBT = $\dfrac{1}{2}\times BS*BT$ = $\dfrac{1}{2}\times 10*10$ = 50 cm$^2$
Therefore, the area of hexagon PQRSTU = 600 – (30+40+50) = 480 cm$^2$.
2) Answer (A)
Let us name various points in the diagram to make it easy to calculate.
From the equation of circle given above, we can see that coordinates of centre of circle O = (0,0) and radius = $a$ units.
Thus, the coordinates of the ends of the circle are : P($a$,0),Q(0,$a$),R($-a$,0),S(0,$-a$)
Let us consider the point E. It is the point of intersection of the tangent AB and the circle. Thus we know that $\angle$EOB = $45^o$
So, if we draw the line OE, we know the slope of line ie $45^o$ => m = 1
Thus, equation of line OE (line going through origin of slope 1) : $y-0 = 1(x-0) \Rightarrow x=y $
The coordinates of E can be found out by finding the solution of the equation of the circle and the equation of OE.
Solving : Putting $x=y$ in equation of circle,
$x^2+x^2 = a^2 \Rightarrow 2x^2 = a^2 \Rightarrow x^2 = \dfrac{a^2}{2} \Rightarrow x = \dfrac{a}{\sqrt{2}} $ and $y = \dfrac{a}{\sqrt{2}} $
Since the tangent is perpendicular to line OE, we know that its slope is $135^o$ ie m’=-1
To find equation of AB, we need to find equation of line going through E with a slope of -1 :
$y-\dfrac{a}{\sqrt{2}} = -1(x-\dfrac{a}{\sqrt{2}}) \Rightarrow y-\dfrac{a}{\sqrt{2}}+x-\dfrac{a}{\sqrt{2}} = 0$
$ \Rightarrow x+y = 2 \times \dfrac{a}{\sqrt{2}} = \sqrt{2}a$
Putting $x=0$ in the equation, we get $y=\sqrt{2}a$ and putting $y=0$ in the equation, we get $x=\sqrt{2}a$
This gives us the coordinates of points A and B : $A(\sqrt{2}a,0)$ and $B(0,\sqrt{2}a)$
Using symmetry, we can see that the triangles are congruent ie $\triangle$AOB = $\triangle$BOC = $\triangle$COD = $\triangle$AOD
Thus by symmetry, we know that the shaded region is same as top half of the larger square ABCD which is also double of the area of $\triangle$AOB
So, area of $\triangle$AOB = $\dfrac{1}{2} \times AO \times OB = \dfrac{1}{2} \times \sqrt{2}a \times \sqrt{2}a = a^2$ units
Thus, area of the shaded region = $2 \times (ar\triangle AOB) = 2a^2$ units
3) Answer (A)
Surface area of milk exposed to surrounding is 81*Pi $cm^2$
Let ‘r’ be the radius of the cone formed.
So, Pi*$ r^2$ = 81*Pi
r = 9 cm
Consider following diagram-

Since triangle PQH is similar to triangle ABH, we have
$ \frac{PQ}{PH} = \frac{AB}{AH}$
$ \frac{12}{5+h} = \frac{9}{h}$
12h = 45 + 9h
h = 15 cm
So, volume of milk in the cone = $\frac{Pi*r^2*h}{3}$ = 405*Pi $ cm^3$
Leak rate of milk = 2*Pi $ cm^3$/hour
Time required to completely empty the cone = $\frac{405*Pi}{2*Pi}$ = 202.5 hours
Hence, option A is the right choice.
4) Answer: 5488
The dimensions of the cuboid formed will be:
Length = Breadth = $42-2a$ cm
Height = $a$ cm
Volume = $a(42-2a)^2$ cc
We can use the AM >= GM property to maximize the volume.
Let’s consider three parts such that they result in a constant term.
Let these three parts be a, (42-2a)/4, (42-2a)/4.
The arithmetic mean of these three would be {a + (42-2a)/4 + (42-2a)/4}/3 = 7
The geometric mean of these three terms will be ${(a*(\frac{42-2a}{4})^2})^{(\frac{1}{3})}$
A.M has to be greater than or equal to the G.M.
$ 7 \geq {(a*(\frac{42-2a}{4})^2})^{(\frac{1}{3})}$
$ 343 \geq {a*(\frac{42-2a}{4})^2}$
=> $ a*(42-2a)*(42-2a) \leq 343*16$
=> a*(42-2a)*(42-2a) $ \leq $ 5488
LHS is nothing but the volume of the resultant cuboid.
Hence, the maximum value of the volume would be 5488.
5) Answer (A)
The arrangement of the sphere is as shown in the figure.

In this figure AC is the body diagonal of the cube and the centre of spheres lie on this body diagonal.
Hence AC = $8\sqrt{3}$
In APOE
OP = OE = r
Angle OPA = Angle OEA = Angle EAP = 90
APOE is a square.
Don’t take AO = $\sqrt{3} r$ as we are dealing with a 3 dimensional figure.
AO =$\sqrt{3} r$
Similarly if we consider the centre of other circle as O1 then CO1=$\sqrt{3} r$
AC = $\sqrt{3}r+\sqrt{3}r+r+r$ = $[2+2\sqrt{3}] r$
AC = $8\sqrt{3}$
$[2+2\sqrt{3}]$r = $8\sqrt{3}$
r =$\frac{8\sqrt{3}}{2+2\sqrt{3}}$
Volume of the sphere =$\frac{4\pi r^3}{3}$
= $\frac{4\pi [8\sqrt{3}]^3}{3(2+2\sqrt{3})^3}$
6) Answer (B)
Volume of cube = $a^3$ = $4^3$ = 64
Volume of each cuboid = lbh = 3*2*1 = 6
6*n = 64
=> n = 10.67
Therefore at least 11 cuboids are required in order to form a cube of 4 cm.
7) Answer (B)
Let ABCD be a square of side 10. Mark a point L which is at 2cm from A on the line AB. Similarly, mark a point m which is 2 cm from B on line AB proceeding in a similar manner, mark n and o on BC, p and q on CD, and r and s on AD such that s is 2 cm away from A on AD.
So we are removing the squares of side 2 from each of the corners. Let the 4 corners of each of these squares be u, v w and x respectively.
So after removing the squares, the figure which will remain is ‘sulmnowpqxr’
Now when we make a cuboid out of it, the length of the cuboid will be lm, breadth will be SR and height will be ul
So the required dimensions are 6*6*2 = 72.
8) Answer (B)
CD passes through the centre of the circle. Therefore, CD must be the diameter of the circle.
Length of CD = 12 cm
=> Radius of the circle = 6 cm.
Length of AB = 6 cm.

If we connect AB to the centre of the circle, we will get an equilateral triangle (All 3 sides will be 6 cm).
Now, let us join A and D and B and D.
$\angle AOB$ = 60ᵒ (Since triangle AOB is an equilateral triangle).
$\angle AOB$ and $\angle ADB$ are subtended by the same chord, $AB$.
Therefore, $\angle ADB$ = 30ᵒ (Angle subtended by a chord on the circumference is half of the angle subtended by the same chord on the centre).
Now, in triangle AOB, AO = BO= 6 cm (Radii of the circle).
$\angle ADO$ = 30ᵒ/2 = 15ᵒ (Since the figure is symmetrical about CD).
=> $\angle OAD$ = 15ᵒ (Since triangle AOD is isosceles).
Therefore, $\angle AOD$ = 180ᵒ – 15ᵒ – 15ᵒ = 150ᵒ.
Area of triangle AOD = 0.5*r*r*sin 150ᵒ
= 0.5*6*6*0.5
= 9 $cm^2$
Area of the figure AOBD = 2* Area of triangle AOD
= 2*9
= 18 $cm^2$
Therefore, option B is the right answer.
9) Answer (B)
It is given that one of the internal angles is three times the adjacent angle
Also, we know that sum of adjacent angles in a rhombus is 180°.
So, the angles will be 45° and 135°
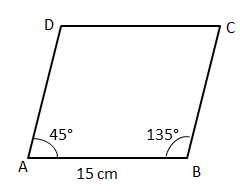
We know that diagonal of rhombus divides it in two triangles of equal area. So, if we find the area of one triangle, we will get the area of rhombus by doubling it.
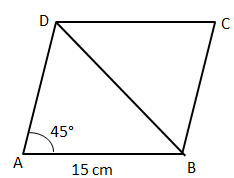
Area of one triangle = $\frac{1}{2}$ * product of adjacent sides * sin$\theta$
Where $\theta$ is included angle
Or, area of one triangle = $\frac{1}{2}$ * 15 * 15 * sin45° = $\frac{225}{2\sqrt{2}}$
Hence, area of the rhombus = $\frac{450}{2\sqrt{2}}$
We know that area of rhombus = $\frac{1}{2}$ * product of diagonals
So, product of diagonals = 2 * Area of rhombus = $\frac{450}{\sqrt{2}}$
10) Answer (D)
Consider following diagram where centre of circle A is ‘A’ and centre of circle B is ‘B’ –

Radius of circle A = 24/2 = 12
Let the radius of circle B = r
Triangle ABC is a right angle triangle
Length of side AB = 12 + r
Length of side AC = 27 – 12 – r = 15 – r
Length of side CB = 12 – r
Applying Pythagoras theorem, we get,
(12 + r)^2 = (15 – r)^2 + (12 – r)^2
r^2 + 24 r + 144 = 2 r^2 – 54 r + 369
r^2 – 78r + 225 = 0
r = 3 or r = 75
r cannot be 75.
Thus r = 3 cm
Area of the rectangle leaving the circle = 24*27 – $\pi * (12^2 + 3^2)$ = 648 – 480.86 = 167.14 $cm^2$
Hence, option D is the right choice.
11) Answer (B)
The isometric view of the cutting plane is shown:
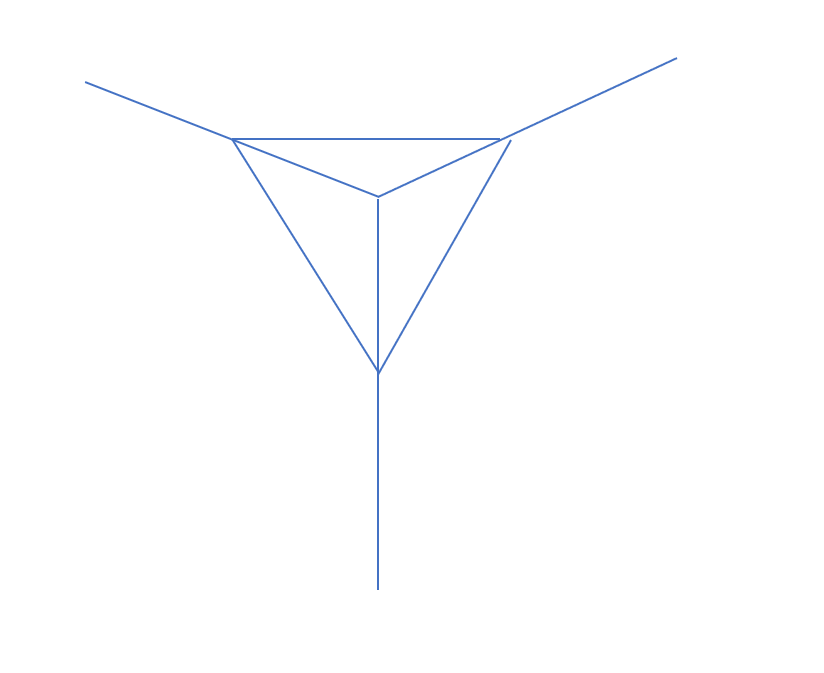
The cut portion consists of 3 isosceles right triangles of sides $4, 4, 4\sqrt{2}$ and one equilateral triangle of side $4\sqrt{2}$.
The surface area will be equal to the area of these 4 triangles.
Area of isosceles triangle = $0.5 * 4 * 4$ = 8
Area of 3 triangles = 24
Area of equilateral triangle = $\frac{\sqrt{3}}{4} * (4\sqrt{2})^2$ = $8\sqrt{3}$
Hence, surface area = $24 + 8\sqrt{3}$
12) Answer (E)
It is given that the length of the diagonals are in 3:4. Let ‘3x’, and ‘4x’ be the lengths of semi-diagonals as shown in the figure. We know that diagonals of a rhombus intersect each other perpendicularly.
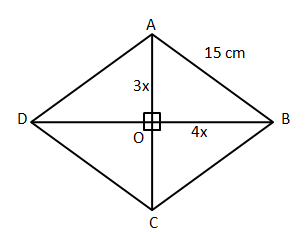
In right angle triangle AOB,
$AB^2=AO^2+BO^2$
$\Rightarrow$ $AB= \sqrt{AO^2+BO^2}$
$\Rightarrow$ $AB= \sqrt{(3x)^2+(4x)^2}$
$\Rightarrow$ $15= 5x$
$\Rightarrow$ $x= 3$cm.
Therefore, we can say that the length of diagonals = 6x and 8x or 18 and 24 cm.
Hence, the area of the rhombus = $\dfrac{1}{2}*18*24$ = 216 cm$^2$. Therefore, option D is the correct answer.
13) Answer (B)
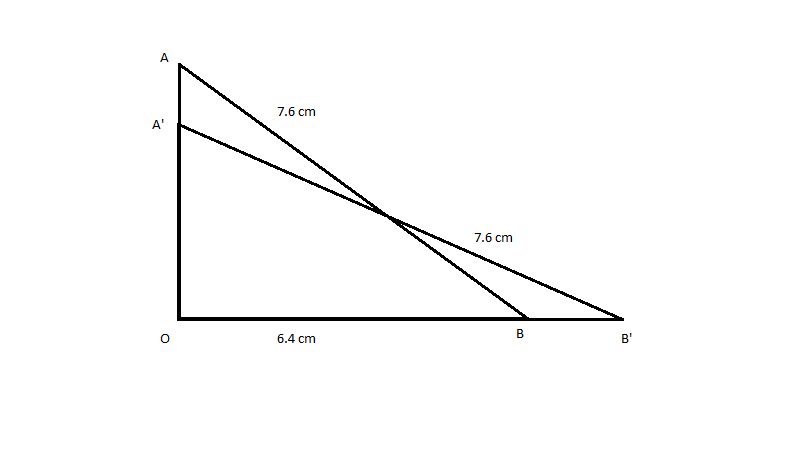
The starting position of ladder is AB.
AB = 7.6 cm and OB = 6.4 cm
Applying Pythagoras Theorem in $\triangle$ AOB
$OA^{2}$ + $OB^{2}$ = $AB^{2}$
OA = 4.10 cm
Now ladder top slips by 1.2 cm, the new position of ladder becomes A’B’
OA’ = 4.10 – 1.2 = 2.9 cm
Applying Pythagoras Theorem in $\triangle$ A’OB’
$OA’^{2}$ + $OB’^{2}$ = $A’B’^{2}$
OB’ = 7.02 cm
Hence, the foot of the ladder is shifted by approximately OB’ – OB = 0.6cm
14) Answer (D)
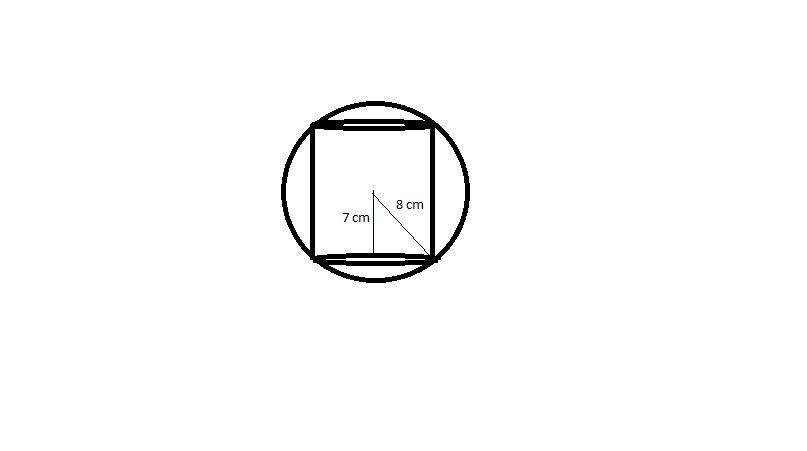
The radius of sphere is 8 $cm$. Then applying Pythagoras, the radius of base of cylinder is $\sqrt{15}$ $cm$
The height of cylinder is given as 14 $cm$. Volume of cylinder is $\pi$ $r^{2}$h
$\frac{22}{7}$* 15*14 = 660 $cm^3$
15) Answer (C)
It is given that the radius of cylinder = 6 cm. The rectangular solid with a square base is placed in the cylinder such that each of the corners of the solid is tangent to the cylinder wall.
Therefore, the diagonal of square base = the diameter of circular base
Hence, a$\sqrt{2}$ = 2*6 = 12 => a = $6\sqrt{2}$ cm.
The volume of water = Volume of the cylinder – Volume of the rectangular solid
$\Rightarrow$ $\pi*6^2*24$ – $(6\sqrt{2})^2*20$
$\Rightarrow$ $864*\pi – 1440$
$\Rightarrow$ $288(3\pi – 5)$
16) Answer (D)
When the paper is rolled along its length, the circumference of the cylinder formed is equal to the length and the height is equal to the breadth of the rectangle.
Let ‘r’ be the radius and ‘h’ be the height of the cylinder formed.
$2\pi*r = 22$ and h = 10
Hence, the volume of the cylinder = $\pi*r^2*h$ = $\dfrac{22}{7}*(7/2)^2*10$ = 385 $cm^3$.
17) Answer (C)
Area of Triangle ABC = $\frac{1}{2}$*$AB*BC *\sin B$
The area will only be maximum when $\sin B$ is maximum.
i.e. B =90°
Hence, AC= $\sqrt{AB^{2} +BC^{2}} $
AC = $\sqrt {7^{2}+8^{2}}$
AC = $\sqrt{113}$
18) Answer (C)
The figure will be as shown below.

Let the side of the square be ‘x’
It is known that AP = 4.5 cm
So AQ = (x-4.5) cm
The area of the triangle AQR will be
$\frac{1}{2}*x*(x-4.5)$
This can be equated to 50 $cm^2$
So we get,
$x(x-4.5)=100$
$=>2x^2-9x-200=0$
$=>(2x-25)(x+8)=0$
As $x$ cannot be negative it has to be 12.5 cm
Area of the square will be = 12.5*12.5 = 156.25 $cm^2$
Hence Option C.
19) Answer (C)
The solid formed will be of the shape where two identical cones are joined from their bases.
The height of cone is half the length of the longer diagonal and the radius of the cone is half the length of the shorter diagonal.
Let the length of the larger diagonal be $l$
$6^2$= $(\frac{l}{2})^2$ +$\sqrt{11}^{2}$
$l =10$
Volume of the cone = $\frac{1}{3}$*$\pi $*$\sqrt{11}^{2}$*$\frac{10}{2}$ = $\frac{55\pi}{3}$
Total Volume = $2$*$\frac{55\pi}{3}$
Total Volume of the solid = $\frac{110\pi}{3}$
20) Answer (C)

The area of triangle POQ = ½ x PQ x h1 = 24
h1 = 24/2 = 12 cm
Triangle POQ is similar to triangle ROS(PQ || SR), thus PQ/SR = h1/h2
=> h2 = h1 x 6/4 = 18cm
Thus, the height of the trapezium = 18 + 12 = 30 cm
The area of the trapezium PQRS = ½ x (h)(PQ + SR) = ½ x (30) x (10) = 150 $cm^2$
DOWNLOAD APP FOR RRB FREE MOCKS
We hope this Mensuration questions for RRB NTPC Exam will be highly useful for your preparation.






