RRB NTPC Geometry Questions PDF
Download RRB NTPC Geometry Questions and Answers PDF. Top 25 RRB NTPC Geometry questions based on asked questions in previous exam papers very important for the Railway NTPC exam.
Download RRB NTPC Geometry Questions PDF
20 RRB NTPC Mocks – Just Rs. 149
RRB NTPC Previous Papers [Download PDF]
Question 1: Find the curved surface area of cone of radius 21cm and slant height 42cm ?
a) 2882
b) 2552
c) 2772
d) 2662
Question 2: Which of the following points, lies on the line perpendicular to x-y = 0 ?
a) (2 , -3)
b) (3 , 2)
c) (-3 , 3)
d) (-2 , -2)
Question 3: Rajiv Gandhi International Cricket Stadium, Hyderabad, has boundary length of 70 meters from the center of the pitch, After winning the match, players are running with joy along the boundary line. Find the distance run by by a player after the completion of 2.5 rounds ?
a) 900 m
b) 1000 m
c) 1100 m
d) 1200 m
Question 4: Find the point of intersection of medians of a triangle having vertices A(1,2), (2,3), (3,1) ?
a) (1,1)
b) (2,1)
c) (1,2)
d) (2,2)
Question 5: Find the slope of the line joining A (3, -4) & B (-3, 4) ?
a) -3/4
b) 3/4
c) -4/3
d) 4/3
Question 6: Find the ratio of the volumes of a sphere of radius 6cm and a cone of height 6cm and radius 4cm ?
a) 9:1
b) 1:9
c) 3:1
d) 1:3
Question 7: Find the length of a tangent, drawn to a circle of radius 4 cm, from a point which is at a distance of 5 cm from the centre ?
a) 4 cm
b) 5 cm
c) 3 cm
d) 2 cm
Question 8: Find the area of trapezium ABCD, AB=7 cm, CD=5 cm & height of trapezium is 4 cm ? It is known that AB is parallel to CD
a) 20 sq.cm
b) 24 sq.cm
c) 28 sq.cm
d) 32 sq.cm
Question 9: Find the slope of a line perpendicular to 5x-3y+2 = 0 ?
a) 5/3
b) -5/3
c) -3/5
d) 3/5
Question 10: Find the maximum volume of the sphere that can be inscribed completely in a cuboid of length 10 cm breadth 8 cm and height 7 cm ?
a) 160 cubic cm
b) 170 cubic cm
c) 180 cubic cm
d) 190 cubic cm
RRB NTPC Previous Papers Download PDF
RRB JE PREVIOUS PAPERS DOWNLOAD
Question 11: The edges of a cuboid are in the ratio 2 : 3 : 4 and its surface area equals 468 sq cm. Find the difference in the length of the longest edge and the shortest edge?
a) 12 cm
b) 3 cm
c) 6 cm
d) 9 cm
Question 12: If the cost of painting a house of 4 walls, having length 6 cm, width 4 cm and height 8 cm, is 480/-. Then find the cost of painting per sq cm?
a) 2/-
b) 2.5/-
c) 3/-
d) 3.5/-
Question 13: A sector of a circle subtends 180 degrees at the center. If the radius of the circle is 7 cm, what is the perimeter of the sector?
a) 46 cm
b) 40 cm
c) 36 cm
d) 30 cm
Question 14: The edges of a cuboid are in the ratio 4 : 3 : 2 and the volume of the cuboid is 648 cubic cm. What is the surface area of the cuboid?
a) 468sq.cm
b) 446sq.cm
c) 424sq.cm
d) 436sq.cm
Question 15: How many cubes of side 2cm can be formed by melting a cuboid of length 6 cm, breadth 4 cm and height 4 cm. ?
a) 12
b) 14
c) 16
d) 18
18000+ Questions – Free SSC Study Material
Download General Science Notes PDF
Question 16: If the length of the side of a square is x and that of an equilateral triangle is x+3. Then find the area of square if the perimeters of square and triangle are same ?
a) 36 sq.units
b) 49 sq.units
c) 81 sq.units
d) can not be determined
Question 17: Find the ratio of the volumes of a cone of height 4cm, radius 6cm and a cylinder of height 6cm and radius 4cm ?
a) 1:2
b) 2:1
c) 2:3
d) 3:2
Question 18: Find the ratio of the heights of cylinders of same radius, if ratio of their volumes are 2:3 ?
a) √2 : √3
b) 3:2
c) 2:3
d) √3 : √2
Question 19: The four walls of a house of height 5m, width 7m, length 10m, are to be painted. Assume that the ceiling and floor are not to be painted. Find the cost of painting if painter charges Rs.2 per sq.m ?
a) 210/-
b) 420/-
c) 520/-
d) 340/-
Question 20: A footpath of uniform width is constructed around a square field of side 6 m. The area of the foot path is 28 sq.m. Then find the width of the footpath ?
a) 2 m
b) 1.5 m
c) 1 m
d) 0.5 m
Question 21: There is a cylindrical metal tube of length 5.5 m which is open at both the ends. The external diameter of the tube is 2.8m and the thickness is 0.4m. What is the volume of the metal used in the tube?
a) $\frac{108.78}{7}$ cu.cm.
b) $\frac{134.54}{7}$ cu.cm.
c) $\frac{116.16}{7}$ cu.cm.
d) $\frac{122.32}{7}$ cu.cm.
Daily Free RRB Online Tests for RRB Exams
Question 22: Each interior angle of a regular polygon is 144°. Find the number of sides of the polygon?
a) 8
b) 9
c) 10
d) 12
Question 23: Ram wants to paint his hall. The room is rectangular in shape. Ram does not want to paint the ceiling or the floor. The dimensions of the room is 10 m x 8 m x 6 m. The ceiling has the maximum area among all the surfaces. If the cost of painting 1 square metre is Rs.7, how much should Ram spend to paint the hall?
a) Rs. 1512
b) Rs. 1348
c) Rs. 1728
d) Rs. 1624
Question 24: If the perimeter of an equilateral triangle is 30 meters, what is its height?
a) 9.66 mts
b) 8.66 mts
c) 7.66 mts
d) 6.66 mts
Question 25: A and B are complementary angles and A, B and C are supplementary angles. What is the value of C?
a) 0 degrees
b) 45 degrees
c) 90 degrees
d) 180 degrees
Download Current Affairs Questions & Answers PDF
Answers & Solutions:
1) Answer (C)
Curved surface area of cone = $\pi rl = (22/7)(21)(42) = 2772$ sq.cm
So the answer is option C.
2) Answer (C)
the line perpendicular to x-y = 0 is x+y = 0—-(1)
only (-3, 3) satisfies (1)
So the answer is option C.
3) Answer (C)
Radius of ground = 70 m
Distance run in 1 complete round = circumference of ground
Distance run in $2\frac{1}{2}$ complete rounds = $2\frac{1}{2}\times$ circumference of ground = $2.5\times 2\pi r = 2.5\times 2(\frac{22}{7})(70) = 2.5\times 440 = 1100m$
So the answer is option C.
4) Answer (D)
point of intersection of medians of a triangle is centroid.
Centroid = $(\frac{x_1+x_2+x_3}{3} , \frac{y_1+y_2+y_3}{3}) = (\frac{1+2+3}{3} , \frac{2+3+1}{3}) = (2 , 2)$
So the answer is option A.
5) Answer (C)
$Slope = \frac{y_2-y_1}{x_2-x_1} = \frac{4+4}{-3-3} = -8/6 = -4/3$
So the answer is option C.
6) Answer (A)
Volume of sphere = $\frac{4}{3}\pi r^3 = \frac{4}{3} \pi (6)^3 = 288\pi$
Volume of cone = $\frac{1}{3}\pi r^2 h = \frac{1}{3}\pi (4)^2(6) = 32\pi$
Ratio = $\frac{288\pi}{32\pi} = 9/1$
So the answer is option A.
7) Answer (C)
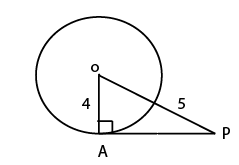
From the diagram,
$l = \sqrt{5^2-4^2} = 3$
So the answer is option C.
8) Answer (B)
Area of trapezium = $\frac{1}{2}(a+b)h = \frac{1}{2}(7+5)(4) = 24sq.cm$
So the answer is option B.
9) Answer (C)
Slope of given line = 5/3
Slope of a line perpendicular to given line = -3/5
So the answer is option C.
10) Answer (C)
Diameter of sphere = smallest of (10, 8, 7) = 7 cm
Volume of sphere = $\frac{4}{3}\pi r^3 = \frac{4}{3}\times\frac{22}{7}\times(7/2)^3 \approx 180$ cubic cm
So the answer is option C.
11) Answer (C)
Let the edges are 2x, 3x, 4x
Total surface area of cuboid = 468 sq.cm
$2[(2x)(3x)+(3x)(4x)+(4x)(2x)] = 468$
$2[6x^2+12x^2+8x^2] = 468$
$2[26x^2] = 468$
$x^2 = 9$
x = 3
Edges are 2x, 3x, 4x i.e; 6cm, 9cm, 12cm
difference in the length of longer edge and shorter edge = 12 – 6 = 6 cm
So the answer is option C.
12) Answer (C)
Lateral surface area = 2h(l+b) = 2(8)(6+4) = 160sq.cm
Let x be the cost of painting per unit area,
Total cost of painting = 480
160x = 480
x = 3/-
So the answer is option C.
13) Answer (C)
Central angle of a sector is 180º i,e; the sector is semi-circle
Perimeter = $\pi r + 2r = (22/7)(7) + 2(7) = 22 + 14 = 36$
So the answer is option C.
14) Answer (A)
Let edges are $4x, 3x, 2x$
Volume = 648
$(4x)(3x)(2x) = 648$
$24 x^3 = 648$
$x^3 = 27$
$x = 3$
Its edges are 12, 9 & 6
Surface area = 2(lb+bh+hl) = 2(108+54+72) = 468sq.cm
So the answer is option A.
15) Answer (A)
no of cubes = (vol.of cuboid)/(vol.of cube) = (6*4*4)/(2*2*2) = 96/8 = 12
So the answer is option A.
16) Answer (C)
4x = 3(x+3)
4x = 3x+9
x = 9
Area of square = x² = 9² = 81 sq.units
So the answer is option C.
17) Answer (A)
Volume of Cone = $\frac{1}{3}\pi r^2h = \frac{1}{3}\pi (6)^2(4) = 48 \pi$
Volume of Cylinder = $\pi r^2h = \pi (4)^2(6) = 96 \pi$
Ratio = $48\pi : 96\pi = 1 : 2$
So the answer is option A.
18) Answer (C)
Volume of cylinder = $\pi r^2 h$
$\frac{h_1}{h_2} = \frac{V_1}{V_2} = \frac{2}{3}$
So the answer is option C.
19) Answer (D)
Surface area of 4 walls of a enclosed room = [2l+2b]*h = [2(10)+2(7)]*(5) = [34]*5 = 170 sq.m
Cost of painting of 1 sq.m = 2/-
Cost of painting of 170 sq.m = 170*2 = 340/-
So the answer is option D.
20) Answer (C)
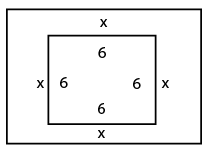
Let x be the width of the path
Area of square filed = 36 sq.m
Then side of the square = 6m
Total area = 36+28 = 64sq.m
(6+2x)(6+2x) = 64
(6+2x)(6+2x) = 8*8
6+2x = 8
x = 1
So the answer is option C.
21) Answer (C)
Let R and r be the outer and inner radius of the cylinder.
Height, h = 5.5 m
R = 2.8/2 = 1.4m and r = 1.4 – 0.4 = 1m
Volume of the metal = $Pi * R^2 * h – Pi * r^2 * h$
= $ Pi * 1.4^2 * 5.5 – Pi * 1 * 5.5$
= $ (1.96 – 1) * \frac{22}{7} * 5.5$
= $\frac{116.16}{7}$ cu.cm.
Hence, option C is the right choice.
22) Answer (C)
We know that for a n sided regular polygon, each angle will be 180*(n – 2)/n
We have been given that 180*(n – 2)/n = 144
=> 180n – 360 = 144n
=> 36n = 360 => n = 10
Hence, the polygon has 10 sides.
23) Answer (A)
Excluding the ceiling and the floor, there will be four surfaces to be painted. The area of the 6 surfaces are 80 sq.m , 80 sq.m, 60 sq.m, 60 sq.m, 48 sq.m and 48 sq.m. The ceiling has the maximum area. Therefore, the floor must also have the maximum area. Leaving these 2 surfaces, the surface area to be painted is 60+60 + 48+48 = 216 sq.m
Cost of painting this area = 216*7 = Rs. 1512.
Therefore, option A is the right answer.
24) Answer (B)
The length of each side = 30/3 = 10 metres.
So, we can observe from the diagram below that the height = $\sqrt{10^2-5^2}$
=8.66 mts
25) Answer (C)
Given A + B = 90 degrees. …. (1)
A + B + C = 180 degrees….. (2)
So, from (1) and (2), C = 90 degrees.
DOWNLOAD APP FOR RRB FREE MOCKS
We hope this Geometry questions for RRB NTPC Exam will be highly useful for your preparation.







